 by Joy Christian » Mon Aug 04, 2014 10:45 am
by Joy Christian » Mon Aug 04, 2014 10:45 am
Hi Jay,
I can provide a formal argument. The detailed analysis of the problem is another matter.
Formally the double slit experiment is no different from any other experiment. In the quantum mechanical description we begin with an initial state such as

,
where 1 and 2 label the two slits. Next we look for a self-adjoint operator, say
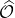
, representing the observable quantities. The expectation value of this operator in the above state,

, then provides the predictions of what will be observed on the screen beyond the slits.
Let me now generalize this prescription to any physical system, in any initial state, for any observable, as follows.
Suppose we consider an arbitrary quantum state
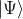
and the corresponding self-adjoint operator
)
in some Hilbert space
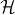
, parameterized by an arbitrary number of
local parameters
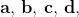
etc. Note that I am imposing no restrictions on the state
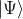
, or on the size of the Hilbert space
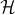
. In particular,
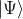
can be as entangled or un-entangled as one may like, and
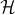
can be as large or small as one may like (in the case of the double slit there is no entanglement, for example). The quantum mechanical expectation value of the operator
)
in the state
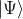
would then be
\, =\,\text{Tr}\left\{{W}\,{\cal\widehat O}({\bf a},\,{\bf b},\,{\bf c},\,{\bf d},\,\dots\,)\right\})
,
where
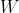
is a statistical operator of unit trace representing the state. Now I have shown that the quantum correlation predicted by this expectation value can always be reproduced as local and realistic correlation among a set of points of a parallelized 7-sphere, by following a procedure very similar to the one discussed above for the 3-sphere. In fact, I have proved the following theorem:
Every quantum mechanical correlation can be understood as a deterministic, local-realistic correlation among a set of points of a parallelized 7-sphere, specified by maps of the form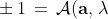: {\rm I\!R}^3\!\times\Lambda\longrightarrow {\rm I\!R}^7\!\times\Lambda\longrightarrow S^7 \hookrightarrow{\rm I\!R}^8)
.
The proof of this theorem can be found in
this paper.
Admittedly, this is quite a formal argument. But it is now possible to fill in the details for the case of the double slit experiment.
Joy
Hi Jay,
I can provide a formal argument. The detailed analysis of the problem is another matter.
Formally the double slit experiment is no different from any other experiment. In the quantum mechanical description we begin with an initial state such as
[tex]|\Psi\rangle = \frac{1}{\sqrt{2}} \left\{ |1\rangle + |2\rangle \right\}[/tex],
where 1 and 2 label the two slits. Next we look for a self-adjoint operator, say [tex]\cal{\widehat O}[/tex], representing the observable quantities. The expectation value of this operator in the above state, [tex]\langle\Psi|{\cal{\widehat O}}| \Psi \rangle[/tex], then provides the predictions of what will be observed on the screen beyond the slits.
Let me now generalize this prescription to any physical system, in any initial state, for any observable, as follows.
Suppose we consider an arbitrary quantum state [tex]|\Psi\rangle[/tex] and the corresponding self-adjoint operator [tex]\cal{\widehat O}({\bf a},\,{\bf b},\,{\bf c},\,{\bf d},\,\dots\,)[/tex] in some Hilbert space [tex]\cal H[/tex], parameterized by an arbitrary number of [u]local[/u] parameters [tex]{{\bf a},\,{\bf b},\,{\bf c},\,{\bf d},}[/tex] etc. Note that I am imposing no restrictions on the state [tex]|\Psi\rangle[/tex], or on the size of the Hilbert space [tex]{\cal H}[/tex]. In particular, [tex]|\Psi\rangle[/tex] can be as entangled or un-entangled as one may like, and [tex]{\cal H}[/tex] can be as large or small as one may like (in the case of the double slit there is no entanglement, for example). The quantum mechanical expectation value of the operator [tex]{\cal\widehat O}({\bf a},\,{\bf b},\,{\bf c},\,{\bf d},\,\dots\,)[/tex] in the state [tex]|\Psi\rangle[/tex] would then be
[tex]{\cal E}_{{\!}_{Q.M.}}({\bf a},\,{\bf b},\,{\bf c},\,{\bf d},\,\dots\,)\, =\,\text{Tr}\left\{{W}\,{\cal\widehat O}({\bf a},\,{\bf b},\,{\bf c},\,{\bf d},\,\dots\,)\right\}[/tex],
where [tex]{W}[/tex] is a statistical operator of unit trace representing the state. Now I have shown that the quantum correlation predicted by this expectation value can always be reproduced as local and realistic correlation among a set of points of a parallelized 7-sphere, by following a procedure very similar to the one discussed above for the 3-sphere. In fact, I have proved the following theorem:
[b]Every quantum mechanical correlation can be understood as a deterministic, local-realistic correlation among a set of points of a parallelized 7-sphere, specified by maps of the form[/b]
[tex]\pm\,1\,=\,{\cal A} ({\bf a},\,\lambda): {\rm I\!R}^3\!\times\Lambda\longrightarrow {\rm I\!R}^7\!\times\Lambda\longrightarrow S^7 \hookrightarrow{\rm I\!R}^8[/tex].
The proof of this theorem can be found in [url=http://arxiv.org/abs/1201.0775]this paper[/url].
Admittedly, this is quite a formal argument. But it is now possible to fill in the details for the case of the double slit experiment.
Joy
