FrediFizzx wrote:Hi Jay,
That doesn't really help. In the limit of hbar --> 0, we should be able to recover the classical electrodynamic result of magnetic charge being electric charge times the speed of light. Do you happen to have Dirac's original derivation for the DQC that you could email me? Thanks.
Hi Fred:
Actually, Dirac's paper is posted online at
http://rspa.royalsocietypublishing.org/ ... l.pdf+html. As it happens, I have been very closely re-studying this paper over the last week and am going to add a new section to my paper which very carefully relates Dirac's original work to where I have moved it in the present day. I should have something to share early to middle of this coming week.
I tend to think of the classical limit as the
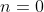
rather than

limit of

, but the main result either way is that you then get

(no monopoles) and
e remains undetermined. You will see from Dirac that the undetermined nature of
e is a major facet (and in his words, disappointment) of his paper. He started out trying to explain the fine structure number 1/137.036 and instead all he got was the lousy t-shirt, er, I mean, this DQC.

To this day people are still at it on the 137 number.
Jay
PS: If you look at surveys of the top theoretical physicists of the 20th century, of course Einstein is in the #1 slot, but #2 can be very contested. I absolutely put Dirac in that position, ahead of Bohr and Heisenberg and other usual suspects. And what he did with monopoles is a significant part of that because I believe that the road to theoretical unification is paved with monopoles and he started that.
