Yablon wrote:In a sense, Ben is correct that it it may boil down to which approach one prefers to take based on taste, because one can get to the same place -- or at least the Lorentz force -- either way.
My momentary concession to "taste," or to Occam's Razor if one prefers, has made me think whether there might be something in what I just posted at
https://jayryablon.files.wordpress.com/ ... apping.pdf to actually
prove the 4D rather than 5D approach to be the one adopted by nature. Not just taste, but empirical proof. And I think I have it, but bear with me as I think out load and ask for the views of anyone else who has a view:
While the invariant metric linear element
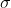
is the
mathematically same in both equations (1) and (4) and via the variation (2) either one leads to the gravitational and Lorentz motion (3), there is one very important
structural difference between
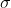
as used in equation (1) versus as used in equation (4). In (1),

is the differential invariant in 4D spacetime and in (4), although the results (3) are mathematically identical once (8), (9) and (10) are applied,

is the differential invariant
in 5D spacetime-plus-gauge-dimension. (I call it the gauge dimension because it contains both
e and
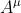
that are part and parcel of the gauge transformations that have a "

" in them.)
I say this for the following reason: Ponder equation (3) carefully. If the

appearing is a 5D invariant, then by (4) this is
not the same as the 4D invariant. If one uses the 4D invariant from (4) alone, one only gets the gravitational geodesic equation without the Lorentz motion. When the 5D invariant is used, the gravitational equation is unchanged, expect for the fact that the gravitational motion is supplemented with the Lorentz motion.
Now, a century and more of experiments have proved beyond doubt that the

of a 4D spacetime is observed as a key invariant everywhere: Lorentz symmetry for relative motion in special relativity, gravitational motion both Newtonian and with the enhancements coming from GR that explain perihelion precession, light bending, and so on. And -- when we observe Lorentz motion -- the same

that appears in all of the foregoing is the one that appears in the Lorentz "force" motion also. In other words,
the Lorentz "force" motion operates and is observed in relation to the same invariant as is everything else that has been observed in relativistic physics since 1905 and 1916. (I put "force" in quotes, because once established as geodesic motion, the Lorentz motion is no longer really a "force.")
So: here is my argument: given that the Lorentz motion is observed to occur in reference to the very same invariant

that is found everywhere else throughout relativistic physics, and given that this

in all these other realms of physics has been firmly established as the invariant of a 4D spacetime and not something of 5D, this means that the

in the Lorentz motion must be a 4D invariant, not a 5D invariant. As a result, the Lorentz motion must originate following the variation (2), from the

in equation (1) and not the

in equation (5).
Consequently, nature proves the 4D linear element of (1) and disproves the 5D element of (5). More generally, even if you develop Kaluza-Klein with some minor variation in relation to what is in
https://jayryablon.files.wordpress.com/ ... apping.pdf, the Lorentz motion occurs in relation to the 5D invariant and that is different from the 4D invariant that has established itself everywhere else in relativistic physics for over a century.
While I have been a big fan of Kaluza-Klein for 30 years, especially for its explanation of matter, I believe I have just disproved it.


Any thoughts? Can you help me strengthen and better articulate this? Or, am I missing something?
FYI, I will be in Mexico for the next week and a half with minimal online access. So if I take awhile to reply, or reply briefly and cryptically, that is the reason.
Jay
[quote="Yablon"]In a sense, Ben is correct that it it may boil down to which approach one prefers to take based on taste, because one can get to the same place -- or at least the Lorentz force -- either way.[/quote]
My momentary concession to "taste," or to Occam's Razor if one prefers, has made me think whether there might be something in what I just posted at https://jayryablon.files.wordpress.com/2016/01/kaluza-klein-mapping.pdf to actually [i]prove[/i] the 4D rather than 5D approach to be the one adopted by nature. Not just taste, but empirical proof. And I think I have it, but bear with me as I think out load and ask for the views of anyone else who has a view:
While the invariant metric linear element [tex]\sigma[/tex] is the [i]mathematically [/i]same in both equations (1) and (4) and via the variation (2) either one leads to the gravitational and Lorentz motion (3), there is one very important [i]structural [/i]difference between [tex]\sigma[/tex] as used in equation (1) versus as used in equation (4). In (1), [tex]d\sigma[/tex] is the differential invariant in 4D spacetime and in (4), although the results (3) are mathematically identical once (8), (9) and (10) are applied, [tex]d\sigma[/tex] is the differential invariant [i]in 5D spacetime-plus-gauge-dimension[/i]. (I call it the gauge dimension because it contains both [i]e[/i] and [tex]A^\mu[/tex] that are part and parcel of the gauge transformations that have a "[tex]+ieA^\mu[/tex]" in them.)
I say this for the following reason: Ponder equation (3) carefully. If the [tex]d\sigma[/tex] appearing is a 5D invariant, then by (4) this is [i]not the same[/i] as the 4D invariant. If one uses the 4D invariant from (4) alone, one only gets the gravitational geodesic equation without the Lorentz motion. When the 5D invariant is used, the gravitational equation is unchanged, expect for the fact that the gravitational motion is supplemented with the Lorentz motion.
Now, a century and more of experiments have proved beyond doubt that the [tex]d\sigma[/tex] of a 4D spacetime is observed as a key invariant everywhere: Lorentz symmetry for relative motion in special relativity, gravitational motion both Newtonian and with the enhancements coming from GR that explain perihelion precession, light bending, and so on. And -- when we observe Lorentz motion -- the same [tex]d\sigma[/tex] that appears in all of the foregoing is the one that appears in the Lorentz "force" motion also. In other words, [i]the Lorentz "force" motion operates and is observed in relation to the same invariant as is everything else that has been observed in relativistic physics since 1905 and 1916[/i]. (I put "force" in quotes, because once established as geodesic motion, the Lorentz motion is no longer really a "force.")
So: here is my argument: given that the Lorentz motion is observed to occur in reference to the very same invariant [tex]d\sigma[/tex] that is found everywhere else throughout relativistic physics, and given that this [tex]d\sigma[/tex] in all these other realms of physics has been firmly established as the invariant of a 4D spacetime and not something of 5D, this means that the [tex]d\sigma[/tex] in the Lorentz motion must be a 4D invariant, not a 5D invariant. As a result, the Lorentz motion must originate following the variation (2), from the [tex]d\sigma[/tex] in equation (1) and not the [tex]d\sigma[/tex] in equation (5).
Consequently, nature proves the 4D linear element of (1) and disproves the 5D element of (5). More generally, even if you develop Kaluza-Klein with some minor variation in relation to what is in https://jayryablon.files.wordpress.com/2016/01/kaluza-klein-mapping.pdf, the Lorentz motion occurs in relation to the 5D invariant and that is different from the 4D invariant that has established itself everywhere else in relativistic physics for over a century.
While I have been a big fan of Kaluza-Klein for 30 years, especially for its explanation of matter, I believe I have just disproved it. :) :(
Any thoughts? Can you help me strengthen and better articulate this? Or, am I missing something?
FYI, I will be in Mexico for the next week and a half with minimal online access. So if I take awhile to reply, or reply briefly and cryptically, that is the reason.
Jay
