SciPhysicsForums.com

by **Yablon** » Tue Jun 11, 2019 5:35 am

gill1109 wrote:Nowadays experimenters do routinely simultaneously "measure" non-commuting observables on one and the same system.

I'd be interested in understanding what it means to simultaneously "measure" values of non-commuting operators. And since the "example" I am starting with is intrinsic spin, I'd like to see whether someone can really measure spin up or down along the z axis, and simultaneously measure the spin vector azimuth $\varphi$ in the xy plane, i.e., the angle around the spin cone illustrated in viewtopic.php?f=6&t=383#p8723.

gill1109 wrote:By all means lets start to talk about the "reality" of those quantities which according to your interpretation of conventional QM "cannot be observed". I'm right now at a conference where 60 people are talking full time a whole week exactly on the question what "realism" should mean and what "locality" should mean and what "randomness" is. There are very very exciting new developments. And it seems as though there are more interpretations around than every before.

Good! This is where I wanted to get to. I think we should start with "reality," but far from end there. Also on the table should be completeness, observability, uncertainty, predictability with certainty, locality, and hidden variable (which several of us argued about yesterday). And of course, the intertwining of all of these. I think I will start a separate, new thread devoted to "definitions" of these key concepts and how they are interrelated, and the underlying principles we use to fashion these definitions.

by **gill1109** » Mon Jun 10, 2019 9:45 pm

I'm not very interested in the conventional dogmas of conventional QM. Things have progressed a lot in the last 50 years. There are more things you can measure. Even conventional QM gives you more options. For instance, what you can also do is ... bring in an independent ancillary system in a fixed state. Let it interact in unitary way with the system of interest. Now measure an observable of the ancillary system. You can also randomise. Toss classical coins or dice and perform different measurements according to the outcome of the randomisation. Nowadays experimenters do routinely simultaneously "measure" non-commuting observables on one and the same system. There are many many more uncertainty relations/uncertainty principles than the original.

By all means lets start to talk about the "reality" of those quantities which according to your interpretation of conventional QM "cannot be observed". I'm right now at a conference where 60 people are talking full time a whole week exactly on the question what "realism" should mean and what "locality" should mean and what "randomness" is. There are very very exciting new developments. And it seems as though there are more interpretations around than every before.

by **Yablon** » Mon Jun 10, 2019 10:53 am

gill1109 wrote:By the way, I do not think we settled the question of what is a correlation. Theories talk about correlations. Experimenters gather date and calculate things which they call correlations. We have to discuss sooner or later what we take as axiom or definition, what we take as heuristic principle, what we mean by chance.

Well, lets go back to viewtopic.php?f=6&t=383#p8702. I just want to know whether the calcuation

$\text{corr}\left( \sigma \cdot \mathbf{a},\sigma \cdot \mathbf{b} \right)=\frac{\operatorname{cov}\left( \sigma \cdot \mathbf{a},\sigma \cdot \mathbf{b} \right)}{\Delta \left( \sigma \cdot \mathbf{a} \right)\Delta \left( \sigma \cdot \mathbf{b} \right)}=\frac{\left\langle \left( \sigma \cdot \mathbf{a} \right)\left( \sigma \cdot \mathbf{b} \right) \right\rangle -\left\langle \sigma \cdot \mathbf{a} \right\rangle \left\langle \sigma \cdot \mathbf{b} \right\rangle }{\Delta \left( \sigma \cdot \mathbf{a} \right)\Delta \left( \sigma \cdot \mathbf{b} \right)}$ (1.17a)

with the standard deviations:

$\Delta \left( \sigma \cdot \mathbf{a} \right)=\sqrt{\left\langle {{\left( \sigma \cdot \mathbf{a} \right)}^{2}} \right\rangle -{{\left\langle \sigma \cdot \mathbf{a} \right\rangle }^{2}}}$
$\Delta \left( \sigma \cdot \mathbf{b} \right)=\sqrt{\left\langle {{\left( \sigma \cdot \mathbf{b} \right)}^{2}} \right\rangle -{{\left\langle \sigma \cdot \mathbf{b} \right\rangle }^{2}}}$ (1.17b)

to derive:

$\text{corr}\left( \sigma \cdot \mathbf{a},-\sigma \cdot \mathbf{b} \right)=-\left\langle \left( \sigma \cdot \mathbf{a} \right)\left( \sigma \cdot \mathbf{b} \right) \right\rangle =-\mathbf{a}\cdot \mathbf{b}$ (1.19)

is a mathematically correct calculation? Yes or no? And if no, why?

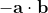
Now, for want of better technical language I would call this a theoretical correlation. And I would agree that there is a second very important calculation to be done which goes event by event, emits a singlet at each event which then splits, which then has a binary value detected by Alice and another one by Bob, and which also arrives at $-\mathbf{a}\cdot \mathbf{b}$ as an expectation value from an average as the number of events approaches infinity. And, if locality is to stand a chance, that second calculation would have show also, that there is no non-local signalling. But we have to walk before we run, so I all want right now is your agreement that there is nothing mathematically amiss in the above calculation.

gill1109 wrote:
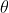
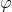
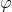
Yablon wrote:III: 8) Finally, with two of the three spherical coordinates $\left\| \lambda \right\|$ and $\theta$ being observable but the third coordinate $\varphi$ being unobservable-in-principle, does everyone agree that there is a good discussion to be had regarding the EPR status of $\varphi$ as an "element of reality"? (We are not having that discussion yet, I just want to see if everyone can get this far on the same page).

...
Now here too something is being slipped in which we are going to have to grapple by the horns. Why should something be "unobservable-in-principle"? A theory may assert that there are no experiments which can directly access certain variables in the theoretical model. But if the theory itself is in question, we can't take that assertion and raise it to the level of dogma.

I recall that Inge Helland (he's a guy, from Norway) has attempted to rewrite and fuse quantum mechanics and statistics through introduction of a new kind of variables. He calls them e-variables ("epistemic conceptual variables"). Get his book, and read it:"Epistemic Processes (A Basis for Statistics and Quantum Theory)" https://www.springer.com/gp/book/9783319950679 which came out very recently.

I took a look at whatever I could see from the online reference, and it does look interesting. But again, let keep the rubber on the road. So I have a few questions, and I will try to stay as mathematical as possible and not use words or phrases (such as "uncertainty principle") which carry too much weighty baggage:

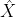
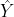
1) From my question III: 4), Do you agree with Robertson that for constant non-commuting operators $\hat{X}$ and $\hat{Y}$ , the standard deviations for those operators have an inequality with the commutator for those operators which is given by:

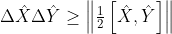
$\Delta \hat{X}\Delta \hat{Y}\ge \left\| \tfrac{1}{2}\left[ \hat{X},\hat{Y} \right] \right\|$ ?

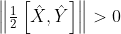
2) For the "same particle," do you agree that if $\left\| \tfrac{1}{2}\left[ \hat{X},\hat{Y} \right] \right\|> 0$ which means that two operators do not commute, that the equation of point 1) above simplifies to:

$\Delta \hat{X}\Delta \hat{Y}> 0$ ?

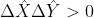
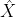
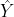
3) Do you agree that it is important to differentiate between whether $\hat{X}$ and $\hat{Y}$ are operators for two different particles or for the same particle?

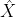
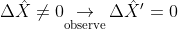
4) Do you agree that for the "same particle," when we actually observe a state value of $\hat{X}$ and therefore acquire a known result, that the a priori non-zero standard deviation, after the observation, goes from $\Delta \hat{X}\ne 0\underset{\text{observe}}{\mathop{\to }}\,\Delta {\hat{X}}'=0$ ? "Before we know to after we know."

5) And here is the main point for critics of "uncertainty" which is really better called "impossibility of simultaneous measurement" (and this is what EPR confine themselves to). Do you agree with the following disproof-by-contradiction?

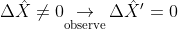
a) Postulate that $\Delta \hat{X}\ne 0\underset{\text{observe}}{\mathop{\to }}\,\Delta {\hat{X}}'=0$ . So we have observed a result from the X operator, and the point 2 equation is now:

$\(\Delta \hat{X}'\Delta \hat{Y}> 0) = (0\cdot\Delta \hat{Y}> 0)$ ?

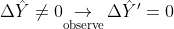
b) Also postulate that $\Delta \hat{Y}\ne 0\underset{\text{observe}}{\mathop{\to }}\,\Delta {\hat{Y}}'=0$ . So we have also simultaneously observed a result from the Y operator.

c) Now the 5)a) equation becomes:

$(0\cdot\Delta \hat{Y}> 0)=(0\cdot\0 > 0)=\mathbf{FALSE}$ .

d) So as a result of 5)c) we have falsified the postulate 5)b) that we observed something from Y simultaneously with X. And so, we cannot simultaneously observe both.

Call it uncertainty, or don't. But unless you care to argue that Robertson's 1) is wrong, we are stuck with the fact that some quantities pertaining to the same particle or interacting system simply cannot be simultaneously measured, when there are non-commuting operators involved.

Anything else, or can we start to talk about how to best understand the "reality" of those quantities which cannot be observed because some other quantity for the same particle or system has already been observed and a second observation would raise a contradiction in the nature of 5)c)?

Jay

by **gill1109** » Sun Jun 09, 2019 9:47 pm

Yablon wrote:III: 8) Finally, with two of the three spherical coordinates $\left\| \lambda \right\|$ and $\theta$ being observable but the third coordinate $\varphi$ being unobservable-in-principle, does everyone agree that there is a good discussion to be had regarding the EPR status of $\varphi$ as an "element of reality"? (We are not having that discussion yet, I just want to see if everyone can get this far on the same page).

By the way, I do not think we settled the question of what is a correlation. Theories talk about correlations. Experimenters gather date and calculate things which they call correlations. We have to discuss sooner or later what we take as axiom or definition, what we take as heuristic principle, what we mean by chance.

Now here too something is being slipped in which we are going to have to grapple by the horns. Why should something be "unobservable-in-principle"? A theory may assert that there are no experiments which can directly access certain variables in the theoretical model. But if the theory itself is in question, we can't take that assertion and raise it to the level of dogma.

I recall that Inge Helland (he's a guy, from Norway) has attempted to rewrite and fuse quantum mechanics and statistics through introduction of a new kind of variables. He calls them e-variables ("epistemic conceptual variables"). Get his book, and read it:"Epistemic Processes (A Basis for Statistics and Quantum Theory)" https://www.springer.com/gp/book/9783319950679 which came out very recently.

by **FrediFizzx** » Sun Jun 09, 2019 12:36 pm

I agree. It is all pretty standard.

by **Yablon** » Sun Jun 09, 2019 9:35 am

OK, following some exchanges with Richard and Heinera, I think we have reached agreement with regard to the matters in rounds I and II. So let's move on to round III. I will start using the "round numbers" for future reference. References below are still to equation numbers in https://jayryablon.files.wordpress.com/ ... -4.1-1.pdf. Here, I'd like to talk about intrinsic spins as an example of the uncertainty principle.

III:1) Does everyone agree that the Pauli matrices have the following non-zero commutator:

$\tfrac{1}{2}\left[ {{\sigma }_{i}},{{\sigma }_{j}} \right]=\tfrac{1}{2}\left[ {{\sigma }_{i}}{{\sigma }_{j}}-{{\sigma }_{j}}{{\sigma }_{i}} \right]=i{{\varepsilon }_{ijk}}{{\sigma }_{k}}\ne 0$ (1.4)

III: 2) If so, do all agree that we can define an operator ${{\Sigma }_{i}}\equiv \tfrac{1}{2}{{\sigma }_{i}}\hbar$ to represent intrinsic spin, and that this will have the following commutator?

$\left[ {{\Sigma }_{i}},{{\Sigma }_{j}} \right]=i{{\varepsilon }_{ijk}}{{\Sigma }_{k}}\hbar$ unnumbered, paragraph before (3.1)

III: 3) Does everyone agree that if all three of the ${{\Sigma }_{i}}\equiv \tfrac{1}{2}{{\sigma }_{i}}\hbar$ are for a single particle or locally-interacting system which we shall call system (A), then the commutator $\left[ {{\Sigma }_{i}}^{\left( A \right)},{{\Sigma }_{j}}^{\left( A \right)} \right]=i{{\varepsilon }_{ijk}}{{\Sigma }_{k}}^{\left( A \right)}\hbar$ will have an Uncertainty Principle relationship which is a consequence of this non-commutation?

III: 4) Does everyone agree that the Robertson uncertainty relation (https://en.wikipedia.org/wiki/Uncertain ... _relations) in general is $\Delta \hat{X}\Delta \hat{Y}\ge \left\| \tfrac{1}{2}\left\langle \left[ \hat{X},\hat{Y} \right] \right\rangle \right\|$ where $\Delta \hat{X}=\sqrt{\left\langle {{{\hat{X}}}^{2}} \right\rangle -{{\left\langle {\hat{X}} \right\rangle }^{2}}}$ and $\Delta \hat{Y}=\sqrt{\left\langle {{{\hat{Y}}}^{2}} \right\rangle -{{\left\langle {\hat{Y}} \right\rangle }^{2}}}$ are the standard deviations of these operators $\hat{X}$ and $\hat{Y}$ ? And that when these operators are constant, the Robertson relation loses the expectation value and simplifies to $\Delta \hat{X}\Delta \hat{Y}\ge \left\| \tfrac{1}{2}\left[ \hat{X},\hat{Y} \right] \right\|$ ?

III: 5) Does everyone agree that when applied to the intrinsic spin operators from point 2) above, that there are three uncertainty relations for the spin of a single particle, one for each space dimension, which are the following?

$\Delta {{\lambda }_{1}}\Delta {{\lambda }_{2}}\ge {{\lambda }_{3}}^{2}=\tfrac{1}{4}{{\hbar }^{2}}\text{ for }\left[ {{\Sigma }_{1}},{{\Sigma }_{2}} \right]=i{{\Sigma }_{3}}\hbar$
$\Delta {{\lambda }_{2}}\Delta {{\lambda }_{3}}\ge {{\lambda }_{1}}^{2}=\tfrac{1}{4}{{\hbar }^{2}}\text{ for }\left[ {{\Sigma }_{2}},{{\Sigma }_{3}} \right]=i{{\Sigma }_{1}}\hbar$ (3.1)
$\Delta {{\lambda }_{3}}\Delta {{\lambda }_{1}}\ge {{\lambda }_{2}}^{2}=\tfrac{1}{4}{{\hbar }^{2}}\text{ for }\left[ {{\Sigma }_{3}},{{\Sigma }_{1}} \right]=i{{\Sigma }_{2}}\hbar$

Note: In the standard deviations have used the eigenvalues of these operators obtained via $\left( {{\Sigma }_{i}}-{{\lambda }_{i}} \right)\left| {{v}_{i}} \right\rangle =0$ , because the standard deviations of the operators are calculated to be equal to the standard deviations of their eigenvalues. So do you agree with that also?

III: 6) Does everyone agree that one way to represent that "act of observing" one of these eigenvalues is to set its standard deviation to zero? And that, say, if we observe $\lambda }_{3}=+1$ while setting $\Delta {{\lambda }_{3}=0$ , the second and third equations in point 5 lead to a result which contradicts any possibility of simultaneously observing $\lambda }_{1}$ and $\lambda }_{2}$ ? And that this is the origin of the so-called "spin cone" for uncertainty / indeterminacy in the spin azimuth $\varphi$ which I diagram in Figure 1 on page 19, also shown right below? And of the common view that spin cannot be simultaneously measured along more than a single axis at a time?

III: 7) Does everyone agree that we can thereby represent the intrinsic spin vector using spherical coordinates with a magnitude $\left\| \lambda \right\|=\tfrac{\sqrt{3}}{2}\hbar$ based on the Casimir operator ${{\Sigma }^{2}}\equiv s\left( s+1 \right)I$ for $s=\tfrac{1}{2}$ , a polar descent angle $\theta =54.736{}^\circ$ for z spin up and $\theta =\pi -54.736{}^\circ$ for z spin down, and an entirely unobservable-in-principle azimuth $\varphi$ ?

III: 8) Finally, with two of the three spherical coordinates $\left\| \lambda \right\|$ and $\theta$ being observable but the third coordinate $\varphi$ being unobservable-in-principle, does everyone agree that there is a good discussion to be had regarding the EPR status of $\varphi$ as an "element of reality"? (We are not having that discussion yet, I just want to see if everyone can get this far on the same page).

Jay

by **FrediFizzx** » Sun Jun 09, 2019 9:03 am

FYI: Bell's original paper is available direct from the publisher now for free.

https://journals.aps.org/ppf/abstract/1 ... zika.1.195
.

by **Yablon** » Sun Jun 09, 2019 8:55 am

Heinera wrote:
Yablon wrote:
Heinera wrote:The point of Bell's definition being broad, is that the hidden variable must include everything that is relevant for the prediction of the outcome, with the exception of the angle setting in the detector. In Bell's setup, the outcome at Alice is a function of two things only: $\vec{a}$ and $\lambda$ . If your variable is not this all-inclusive, it is not a hidden variable in the sense of Bell.

I agree with this, assuming by "prediction of the outcome" you mean explaining how the singlet correlation comes to be $-\mathbf{A}\cdot \mathbf{B}$ .

No, I do not mean that, because the correlations are already very well explained by QM. With "outcome" I (and Bell) meant -1 or +1.

Fair enough, I agree.

by **Heinera** » Sun Jun 09, 2019 8:39 am

Yablon wrote:
Heinera wrote:The point of Bell's definition being broad, is that the hidden variable must include everything that is relevant for the prediction of the outcome, with the exception of the angle setting in the detector. In Bell's setup, the outcome at Alice is a function of two things only: $\vec{a}$ and $\lambda$ . If your variable is not this all-inclusive, it is not a hidden variable in the sense of Bell.

I agree with this, assuming by "prediction of the outcome" you mean explaining how the singlet correlation comes to be $-\mathbf{A}\cdot \mathbf{B}$ .

No, I do not mean that, because the correlations are already very well explained by QM. With "outcome" I (and Bell) meant -1 or +1.

by **Yablon** » Sun Jun 09, 2019 8:20 am

Heinera wrote:The point of Bell's definition being broad, is that the hidden variable must include everything that is relevant for the prediction of the outcome, with the exception of the angle setting in the detector. In Bell's setup, the outcome at Alice is a function of two things only: $\vec{a}$ and $\lambda$ . If your variable is not this all-inclusive, it is not a hidden variable in the sense of Bell.

I agree with this, assuming by "prediction of the outcome" you mean explaining how the singlet correlation comes to be $-\mathbf{A}\cdot \mathbf{B}$ .

by **Heinera** » Sun Jun 09, 2019 8:01 am

Yablon wrote:This is actually a fairly broad definition. I am perfectly content to regard this "vital assumption" as a minimal necessary requirement for a "hidden variable" used in connection with QM correlations between A and B. Also I would even consider more restrictive requirements which tighten this definition, i.e., to entertain the possibility that this definition is insufficiently restrictive, as to how something acquires status as a "hidden variable" to begin with.

[...]

Jay

The point of Bell's definition being broad, is that the hidden variable must include everything that is relevant for the prediction of the outcome, with the exception of the angle setting in the detector, and the mechanism of the detectors (which are encoded in the functions $A$ and $B$ ). In Bell's setup, the outcome at Alice is a function of two things only: $\vec{a}$ and $\lambda$ . If your variable is not this all-inclusive, it is not a hidden variable in the sense of Bell.

by **Yablon** » Sun Jun 09, 2019 6:21 am

Heinera wrote:I guess my reply to Jay is that it's not clear to me where this is going, and whether it will be worth the time to keep following the development.

My issue here is that we need to stick with the definition of a "hidden variable" in the sense of Bell. I could write down the letter $x$ on a piece of paper, bury it in my garden and claim I had a hidden variable, but it would not be what Bell had in mind. The main takeaway from Bell's theorem is that no tweaking of classical theory that retains realism and locality can replicate QM theory. So QM is in some sense fundamentally different. Introducing an extra (and probably superfluous) variable into QM, and calling it "hidden", won't change that fact.

OK, Heinera, let's go the Bell, which you can find online at https://cds.cern.ch/record/111654/files ... 00_001.pdf. From the bottom of page 1 into page 2:

"Let this more complete specification be effected by means of parameters $\lambda$ . It is a matter of indifference in the following whether $\lambda$ denotes a single variable or a set, or even a set of functions, and whether
the variables are discrete or continuous. However, we write as if $\lambda$ were a single continuous parameter. The result A of measuring ${{\vec{\sigma }}_{1}}\cdot \vec{a}$ is then determined by $\vec{a}$ and $\lambda$ , and the result B of measuring ${{\vec{\sigma }}_{2}}\cdot \vec{b}$ in the same instance is determined by $\vec{b}$ and $\lambda$ , and

$A\left( \vec{a},\lambda \right)=\pm 1,\ B\left( \vec{b},\lambda \right)=\pm 1$ (1)

The vital assumption . . . is that the result B for particle 2 does not depend on the setting $\vec{a}$ of the magnet for particle 1, nor A on $\vec{b}$ ."

This is actually a fairly broad definition. I am perfectly content to regard this "vital assumption" as a minimal necessary requirement for a "hidden variable" used in connection with QM correlations between A and B. Also I would even consider more restrictive requirements which tighten this definition, i.e., to entertain the possibility that this definition is insufficiently restrictive, as to how something acquires status as a "hidden variable" to begin with.

Does everyone agree this this as a "statement in principle" of how we define "hidden variables"?

Jay

by **Yablon** » Sat Jun 08, 2019 7:24 pm

gill1109 wrote:
Yablon wrote:
Yablon wrote:1) Using a prepared singlet state, Quantum Mechanics (QM) predicts a strong correlation $corr=-a\cdot b = - cos \theta_{a,b}$ ? And that this has robust empirical support?

2) This correlation in #1 above is stronger, i.e., has a larger numeric magnitude than the linear correlation $corr = -1+2\theta_{a,b}/\pi$ , with $0\le\theta_{a,b}\le \pi$ , at all except 0, 90 and 180 degrees, where they are equal?

3) At, say, $\theta_{a,b}=135^\circ$ , #1 is larger than #2 above by a factor of $\sqrt 2$ which is traceable to the $2\sqrt2$ outer bounds of the CSHS inequality for QM, versus just 2 for linear correlations?

4) One we agree about #1, #2 and #3, we really don't need to talk any further about the inequality, but can just talk about the correlations, because we can all figure out how that translates to the inequality?

5) The prevailing view is that QM is not all of a "local" and "realistic" and "hidden variable" theory, as those terms are generally defined? (I am not asking at the moment for a debate about these terms.)

I am going to assume that everyone agrees on the above and will now go on to round 2. I am focusing on QM, not any other theory. Can we all agree on the following, and if not, why not?

Sorry I wasn't finished with your first round. I agree with #1, #2 and #3; but I disagree with #4.

We don't want to talk *only* about the cosine wave and the triangle wave.

There are many, many more correlation curves allowed by QM and indeed engineered in the lab and used for Bell type experiments. In fact, the Vienna and Boulder experiments very deliberately used a not maximally entangled state. They used the only state which allows you to get away with only 75% detector efficiency. They had just slightly better...

There are many, many more correlation curves allowed by LR (or LHV or LRHV).

Bell's theorem, and Tsirelson's theorem, tell us about the *sets of all correlation curve*s allowed under each of the two theories (QM and LR respectively). One *set* is contained in the other. The famous 2 sqrt 2 comes from choosing a particular metric and then looking for the point in the QM set which is furthest from its own closest LR set. Those two curves - ie solutions of a minimax problem - are indeed the cosine and the triangle wave.

Richard, I agree with what you said about the many correlation curves. Perhaps I should restate my number 4 like this:

On pretty much all else, I was looking for agreement about objective points of science and / or mathematics. In #4 I am really asking for a pedagogical agreement for the discussions we are having, that we all agree to stick with the strongest $-\mathbf{A}\cdot \mathbf{B}$ correlation from the singlet state because that is all we really need as a "laboratory" for discussing the LRHV properties (or not) of QM. Whatever LRHV attributes QM has or does not have for the singlet correlation, it will likewise have or not have for the other correlations. So I would for us to arrive at a pedagogical agreement that we all stay focused on the singlet state:

$\left| {{\varphi }_{0,0}} \right\rangle \equiv \left| s=0,\ {{s}_{z}}=0 \right\rangle =\tfrac{1}{\sqrt{2}}\left( {{\left| \uparrow \right\rangle }^{\left( 1 \right)}}\otimes {{\left| \downarrow \right\rangle }^{\left( 2 \right)}}-{{\left| \downarrow \right\rangle }^{\left( 1 \right)}}\otimes {{\left| \uparrow \right\rangle }^{\left( 2 \right)}} \right)$ (1.1)

I am not in any way suggesting that these other states are irrelevant or uninteresting. Rather I am suggesting that once we resolve the major issues of principle for the singlet, those issues will fall the same way for other prepared states which are not as correlated as the singlet.

In fact, in an earlier draft of https://jayryablon.files.wordpress.com/ ... -4.1-1.pdf I also calculated correlations for the spin 1 triplet prepared states:

$\left\{ \begin{matrix}\left|{{\varphi }_{1,+1}} \right\rangle \equiv \left| s=1,\ {{s}_{z}}=+1 \right\rangle ={{\left| \uparrow \right\rangle }^{\left( 1 \right)}}\otimes {{\left| \uparrow \right\rangle }^{\left( 2 \right)}}\text{ } \\\left|{{\varphi }_{1,0}} \right\rangle \equiv \left| s=1,\ {{s}_{z}}=0 \right\rangle =\tfrac{1}{\sqrt{2}}\left( {{\left| \uparrow \right\rangle }^{\left( 1 \right)}}\otimes {{\left| \downarrow \right\rangle }^{\left( 2 \right)}}+{{\left| \downarrow \right\rangle }^{\left( 1 \right)}}\otimes {{\left| \uparrow \right\rangle }^{\left( 2 \right)}} \right) \\\left|{{\varphi }_{1,-1}} \right\rangle \equiv \left| s=1,\ {{s}_{z}}=-1 \right\rangle ={{\left| \downarrow \right\rangle }^{\left( 1 \right)}}\otimes {{\left| \downarrow \right\rangle }^{\left( 2 \right)}}\text{ } \\\end{matrix} \right.$ also(1.1)

But I decided to pull that out because I felt it would be a distraction from getting to the main issues as directly as possible. I am really trying to stay efficient and not get distracted by anything not directly relevant to the core questions of the LRHV or not properties of QM, or that will merely give answers of principle which are redundant to what we find for the singlet.

Jay

PS: I had a good but long day. After my grandson saw me dive into the pool he got all excited and had me get out and me repeat multiple, multiple times.

So I am exhausted. I do want to pick up on Heinera's question regarding hidden variables, but will need to do so when I am fresh in the morning.

by **FrediFizzx** » Sat Jun 08, 2019 11:00 am

Guys, let's try to stay on topic here. My fault for mentioning that.

Jay, I think everyone agrees with what you have presented so far except for #4. But I think you only want to talk about QM correlations here so please proceed.

by **Joy Christian** » Sat Jun 08, 2019 10:15 am

Heinera wrote:And furthermore, can someone please refrain from this endless plugging of Joy Christian's theory? It's like Cato, who reputedly ended all his speeches in the Roman senate with "Ceterum autem censeo Carthaginem esse delendamt" (Furthermore, I consider that Carthage must be destroyed.)

Can someone please refrain from this endless plugging of the nonsensical "theorem" of Bell? It's like Cato, who reputedly ended all his speeches in the Roman senate with "Ceterum autem censeo Carthaginem esse delendamt" (Furthermore, I consider that Carthage must be destroyed.): (1) https://arxiv.org/abs/1704.02876, (2) https://arxiv.org/abs/1103.1879.

***

by **Heinera** » Sat Jun 08, 2019 9:17 am

FrediFizzx wrote:Perhaps let's not say "replicate QM theory" but a classical local realistic theory that gives the same predictions as QM.
.

Yes, with "replicate" I mean the predictions.

And furthermore, can someone please refrain from this endless plugging of Joy Christian's theory? It's like Cato, who reputedly ended all his speeches in the Roman senate with "Ceterum autem censeo Carthaginem esse delendamt" (Furthermore, I consider that Carthage must be destroyed.)

by **FrediFizzx** » Sat Jun 08, 2019 8:58 am

Heinera wrote:I guess my reply to Jay is that it's not clear to me where this is going, and whether it will be worth the time to keep following the development.

My issue here is that we need to stick with the definition of a "hidden variable" in the sense of Bell. I could write down the letter $x$ on a piece of paper, bury it in my garden and claim I had a hidden variable, but it would not be what Bell had in mind. The main takeaway from Bell's theorem is that no tweaking of classical theory that retains realism and locality can replicate QM theory. So QM is in some sense fundamentally different. Introducing an extra (and probably superfluous) variable into QM, and calling it "hidden", won't change that fact.

Perhaps let's not say "replicate QM theory" but a classical local realistic theory that gives the same predictions as QM. Yes, the hidden variable should be defined in the sense of Bell. Of course, Joy has already accomplished that task. Jay's task here is to get a hidden variable to work directly in QM.
.

by **gill1109** » Sat Jun 08, 2019 6:50 am

OK. We keep on truckin!

There are mathematical definitions, which belong inside “abstract” mathematical structures.

There are the algorithms that data scientists, accountants, shopkeepers, and ordinary folk use, when given a spreadsheet with a heap of numbers.

There has to be some kind of bridge. You could call it meta-physics, or philosophy. The ancient hindus have a story in the Mahabharata about how a prince lost his Kingdom and his wife by gambling. He wandered destitute into the forest where he met a God disguised, I think, as a snake. The God showed him how to count the leaves on a tree by just picking a branch at random, counting the leaves on the branch, and counting the number of branches. The prince (who obviously had already been taught long multiplication) went back and won back his kingdom and his girl by cleverly gambling. He went on to become a famous wise king who no doubt had the necessary skills to raise taxes and raise Armies, and use them wisely, for which some “merely” statistical skills can come in handy, as well as the Insight that randomness can be an asset as well as a horror and an abomination. We humans hate randomness, and we tend to hate maths too. Silly!

The point of this rambling old trucker’s story is that we do have to venture into the foundations of probability, into areas where people are still vehemently fighting one another (Bayesians versus frequentists) much more viciously than in the relatively recent and quiet Bell wars.

by **Yablon** » Sat Jun 08, 2019 6:22 am

gill1109 wrote:OK, maybe I'm a bit old-fashioned. From here on, some old man's ramblings, connecting this all to the very important topic of old Dutch genever. Which I hope to enjoy with many of you when our Symposium and Workshop finally materialises. At which we will be able to admire, on a wall, the genuine and original signatures of Einstein, Lorentz and Ehrenfest.

I too look forward to all that. Let's keep trucking on to the symposium!

Two comments came in overnight, this one from Richard, and another from Heinera. I will reply to Richard here, then hopefully this evening after a busy day with my little grandson, to Heinera.

gill1109 wrote:
Yablon wrote:7) Does anybody have any problem with connecting $-\mathbf{a}\cdot \mathbf{b}$ to a correlation as that term is defined in statistics, to arrive at:

$\text{cor}{{\text{r}}_{q}}_{0,0}\left( a,b \right)=-\mathbf{a}\cdot \mathbf{b}$ (1.20)

Jay: I need to know how you think that the term "correlation" is defined in "statistics" before I can make any comment on this statement.

I do have pretty firm ideas about what "statistics" is and how "correlation" is defined in statistics - I've been teaching statistics to mathematicians, economists, astronomers, and psychologists, and data-scientists, for 45 years.

Richard, I am glad you asked that question. And you are the ideal person to be asking that question given your first rate background in this area. Probably nobody except my own high school chums know or remember this, but in high school, I was allowed by the faculty to teach a course in probability and statistics which was attended by fellow students and even a few teachers. Indeed, my first mathematics love was probability and statistics. Done with this old man's ramblings and on to business.

It is my impression that many discussions of QM correlations focus on the $-\mathbf{a}\cdot \mathbf{b}$ from QM reviewed in my most recent points 1-6 , but not sufficiently on why we can call this a correlation, the point 7 your cited. Is this some unique type of correlation developed for QM? Of course it is not. It is a correlation precisely as that term is used in statistics, and I felt it important, at least in anything I write, to not omit that point.

So, my detailed explanation is in (1.17) through (1.20) of https://jayryablon.files.wordpress.com/ ... -4.1-1.pdf. Here, let me just review the main points:

We start with the standard statistics definition $\text{corr}\left( X,Y \right)=\text{cov}\left( X,Y \right)/\Delta \left( X \right)\Delta \left( Y \right)$ where $\operatorname{cov}\left( X,Y \right)=\left\langle XY \right\rangle -\left\langle X \right\rangle \left\langle Y \right\rangle$ , and the standard deviations are $\Delta \left( X \right)=+\sqrt{\left\langle {{X}^{2}} \right\rangle -{{\left\langle X \right\rangle }^{2}}}$ and $\Delta \left( Y \right)=+\sqrt{\left\langle {{Y}^{2}} \right\rangle -{{\left\langle Y \right\rangle }^{2}}}$ . In sum, the correlation is a normalized covariance.

Because $\left\langle \left( \sigma \cdot \mathbf{a} \right)\left( \sigma \cdot \mathbf{b} \right) \right\rangle =\mathbf{a}\cdot \mathbf{b}$ , point 4, equation (1.15), we want to first calculate the correlation between $X\equiv \sigma \cdot \mathbf{a}$ and $Y\equiv \sigma \cdot \mathbf{b}$ , by plugging these right into the statistical definitions.

This leads to:

$\text{corr}\left( \sigma \cdot \mathbf{a},\sigma \cdot \mathbf{b} \right)=\frac{\operatorname{cov}\left( \sigma \cdot \mathbf{a},\sigma \cdot \mathbf{b} \right)}{\Delta \left( \sigma \cdot \mathbf{a} \right)\Delta \left( \sigma \cdot \mathbf{b} \right)}=\frac{\left\langle \left( \sigma \cdot \mathbf{a} \right)\left( \sigma \cdot \mathbf{b} \right) \right\rangle -\left\langle \sigma \cdot \mathbf{a} \right\rangle \left\langle \sigma \cdot \mathbf{b} \right\rangle }{\Delta \left( \sigma \cdot \mathbf{a} \right)\Delta \left( \sigma \cdot \mathbf{b} \right)}$ (1.17a)

with the standard deviations:

$\Delta \left( \sigma \cdot \mathbf{a} \right)=\sqrt{\left\langle {{\left( \sigma \cdot \mathbf{a} \right)}^{2}} \right\rangle -{{\left\langle \sigma \cdot \mathbf{a} \right\rangle }^{2}}}$
$\Delta \left( \sigma \cdot \mathbf{b} \right)=\sqrt{\left\langle {{\left( \sigma \cdot \mathbf{b} \right)}^{2}} \right\rangle -{{\left\langle \sigma \cdot \mathbf{b} \right\rangle }^{2}}}$ (1.17b)

I know that you, Richard, raised the point to me privately whether you can actually plug the Hermitan matrices $X\equiv \sigma \cdot \mathbf{a}$ and $Y\equiv \sigma \cdot \mathbf{b}$ into the statistical formulas because they are matrices not random variables. But, if you look at (1.17), the only real question is whether each expression inside (1.17) has definite mathematical meaning for these matrices. And if you inspect closely you will see that they do. I discuss this in more detail in the paper draft.

So when we do the calculations and include a minus sign in front of $\sigma \cdot \mathbf{b}$ , we end up with:

$\text{corr}\left( \sigma \cdot \mathbf{a},-\sigma \cdot \mathbf{b} \right)=-\left\langle \left( \sigma \cdot \mathbf{a} \right)\left( \sigma \cdot \mathbf{b} \right) \right\rangle =-\mathbf{a}\cdot \mathbf{b}$ (1.19)

Finally, we make the definition:

$\text{cor}{{\text{r}}_{q}}_{0,0}\left( A,B \right)\equiv \text{corr}\left( \sigma \cdot \mathbf{a},-\sigma \cdot \mathbf{b} \right)=-\mathbf{a}\cdot \mathbf{b}$ (1.20)

recognizing that the minus sign is attributable not to the orientation of the Alice and Bob detectors, but to the oppositely-oriented angular momenta emerging in the two particles which split off out of each singlet prepared state.

Jay

by **Heinera** » Sat Jun 08, 2019 12:40 am

I guess my reply to Jay is that it's not clear to me where this is going, and whether it will be worth the time to keep following the development.

My issue here is that we need to stick with the definition of a "hidden variable" in the sense of Bell. I could write down the letter $x$ on a piece of paper, bury it in my garden and claim I had a hidden variable, but it would not be what Bell had in mind. The main takeaway from Bell's theorem is that no tweaking of classical theory that retains realism and locality can replicate QM theory. So QM is in some sense fundamentally different. Introducing an extra (and probably superfluous) variable into QM, and calling it "hidden", won't change that fact.

SciPhysicsForums.com

Can we all agree on the following about QM correlations?

Post a reply

Expand view Topic review: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?

Re: Can we all agree on the following about QM correlations?