Richard Gill's misinterpretation of my model in his post above can be easily corrected by going through the derivation presented in this
one-page document.
For the sake of argument, let us not worry about the small correction to the function
)
we had been concerned about during the past few weeks.
The question then is: Does eq. (10) in the above derivation hold for
all vectors

or not? If it does, then I am right. If it does not, then Richard Gill is right.
So let us think about this step by step. Note that I begin with the definition of S^3, which is the model for the physical space I have been working with. Next, in eqs. (3) and (4) I have defined two quaternions, as functions of the same vector

. Then the derivation of eq.(10) is quite straightforward, for the choice of the function
)
I have made just above the box of eq. (10). As I mentioned, this choice is immaterial for the present concerns. So, does, then, eq. (10) hold for all vectors

or not? But of course it does. To see this, let us consider a vector
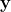
in eqs. (3) and (4) instead of the vector

, and follow through the steps all the way up to eq. (10). So now we have derived eq. (10) again, but with vector
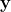
instead of vector

. This means that eq. (10) is valid for at least two vectors, say

and
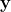
. But what stops us from considering a yet another vector, say

, and re-deriving eq. (10) in terms of this vector

? Well, you got the picture. We can derive eq. (10) for
all vectors

belonging to the tangent space

, as indicated in the definition (11) of the set of complete states. Thus Richard Gill's concerns in his post are entirely unfounded.
Richard Gill's misinterpretation of my model in his post above can be easily corrected by going through the derivation presented in this [url=http://libertesphilosophica.info/blog/wp-content/uploads/2014/02/complete.pdf]one-page document[/url].
For the sake of argument, let us not worry about the small correction to the function [tex]f(\theta_o)[/tex] we had been concerned about during the past few weeks.
The question then is: Does eq. (10) in the above derivation hold for [b][i]all[/i][/b] vectors [tex]{\bf x}[/tex] or not? If it does, then I am right. If it does not, then Richard Gill is right.
So let us think about this step by step. Note that I begin with the definition of S^3, which is the model for the physical space I have been working with. Next, in eqs. (3) and (4) I have defined two quaternions, as functions of the same vector [tex]{\bf x}[/tex]. Then the derivation of eq.(10) is quite straightforward, for the choice of the function [tex]f(\theta_o)[/tex] I have made just above the box of eq. (10). As I mentioned, this choice is immaterial for the present concerns. So, does, then, eq. (10) hold for all vectors [tex]{\bf x}[/tex] or not? But of course it does. To see this, let us consider a vector [tex]{\bf y}[/tex] in eqs. (3) and (4) instead of the vector [tex]{\bf x}[/tex], and follow through the steps all the way up to eq. (10). So now we have derived eq. (10) again, but with vector [tex]{\bf y}[/tex] instead of vector [tex]{\bf x}[/tex]. This means that eq. (10) is valid for at least two vectors, say [tex]{\bf x}[/tex] and [tex]{\bf y}[/tex]. But what stops us from considering a yet another vector, say [tex]{\bf z}[/tex], and re-deriving eq. (10) in terms of this vector [tex]{\bf z}[/tex]? Well, you got the picture. We can derive eq. (10) for [b][i]all[/i][/b] vectors [tex]{\bf x}[/tex] belonging to the tangent space [tex]T_pS^3[/tex], as indicated in the definition (11) of the set of complete states. Thus Richard Gill's concerns in his post are entirely unfounded.
