 by Yablon » Sun Sep 01, 2019 1:10 pm
by Yablon » Sun Sep 01, 2019 1:10 pm
Yablon wrote:Hi all:
You will all know the trigonometric half-angle identity
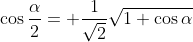
for

.
Can someone please figure out, or does someone know, something similar for the following?
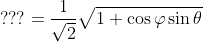
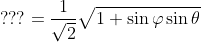
Either point to a trigonometry reference, or please show us how you get there. I am concerned about the body of the functions, more so than the signs.
Thanks,
Jay
OK, what I derived from half angle formulas for sin, cos and tan, via cos^2 and sin^2, is the following:
\sin \frac{\theta }{2}\cos \frac{\theta }{2}})
\sin \frac{\theta }{2}\cos \frac{\theta }{2}})
I would have to say that the original expressions in this case are simpler than those with half angles. Anybody see anything else?
Jay
[quote="Yablon"]Hi all:
You will all know the trigonometric half-angle identity [tex]\cos \frac{\alpha }{2}=+\frac{1}{\sqrt{2}}\sqrt{1+\cos \alpha }[/tex] for [tex]0 \le \alpha \le \pi[/tex].
Can someone please figure out, or does someone know, something similar for the following?
[tex]???=\frac{1}{\sqrt{2}}\sqrt{1+\cos \varphi \sin \theta }[/tex]
[tex]???=\frac{1}{\sqrt{2}}\sqrt{1+\sin \varphi \sin \theta }[/tex]
Either point to a trigonometry reference, or please show us how you get there. I am concerned about the body of the functions, more so than the signs.
Thanks,
Jay[/quote]
OK, what I derived from half angle formulas for sin, cos and tan, via cos^2 and sin^2, is the following:
[tex]\frac{1}{\sqrt{2}}\sqrt{1+\cos \varphi \sin \theta }=\frac{1}{\sqrt{2}}\sqrt{1+\left( 4{{\cos }^{2}}\frac{\varphi }{2}-2 \right)\sin \frac{\theta }{2}\cos \frac{\theta }{2}}[/tex]
[tex]\frac{1}{\sqrt{2}}\sqrt{1+\sin \varphi \sin \theta }=\frac{1}{\sqrt{2}}\sqrt{1+\left( 4\sin \frac{\varphi }{2}\cos \frac{\varphi }{2} \right)\sin \frac{\theta }{2}\cos \frac{\theta }{2}}[/tex]
I would have to say that the original expressions in this case are simpler than those with half angles. Anybody see anything else?
Jay
