I want to bring out something that usually gets obscured in the discussions about the so-called Bell's theorem (we shall not be concerned about trivial variants of such "theorems" by lesser brains---the proponents of such trivialities are advised to promote their nonsense elsewhere).
The dying breed of the Bell mafia (when they are not engaged in spreading despicable violence and terror) routinely demand things from their chastisers that are
not predicted by quantum mechanics, since they have been systematically deprived of valid predictions of quantum mechanics they can pretend to play their game with.
Take, for example, the familiar predictions of the four pairs of Bell-test angles in an EPRB-type experiment:
 = - 0.7071...,)
 = + 0.7071...,)
 = - 0.7071...,)
 = - 0.7071....)
On the face of it there seem to be nothing wrong with these predictions. The expectation value of the products of measurement results when Alice has her polarizer oriented at 0 degrees and Bob has his polarizer oriented at 45 degreees is -0.7071..., and the expectation value of the products of measurement results when Alice has her polarizer oriented at 0 degrees and Bob has his polarizer oriented at 135 degreees is +0.7071..., and so on. But look closely and you will find that this is not really what quantum mechanics actually predicts. If we call Alice's polarization angle
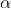
and Bob's polarization angle
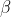
, then quantum mechanics actually predicts
=\langle\Psi|\,\widehat{O}({\alpha},\,{\beta})|\Psi\rangle=-\cos(\alpha - \beta))
where
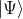
is the singlet state. In other words, quantum mechanics neither knows nor predicts anything about the
absolute polarization angles
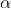
and
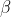
. To be sure experimenters are free to choose them as they will, but quantum mechanics couldn't care less about them. It only cares (i.e., makes predictions) about quantities dependent on the
relative angle
)
between the polarization directions. Thus the above stated four quantitative predictions are actually an overstatement of the facts. The valid predictions of quantum mechanics are only the following two predictions, reducing the above four to two:
 = 45] = - 0.7071...,)
 = 135] = + 0.7071....)
This effectively means that, without violating any predictions of quantum mechanics, we can always set one of the polarization angles to zero and measure the variations in the correlation with respect to that setting. This does not compromise the free will of the experimenter. It only sets a convention for a coordinate system. Thus, for definiteness, we can either set
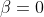
or set
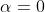
. In the following simulation I show the correlations these two possible conventions lead to:
http://rpubs.com/jjc/16415.
Let me stress again: To demand control over
absolute values of
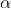
and
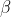
in this simulation is to demand something beyond the confines of quantum mechanics, even if experimenters may have such a control. Thus when the Bell mafia make such demands they are as usual being themselves---i.e., being sore losers and dishonest.
Moreover, it is important to note that in the above simulation there is no filter of any kind---i.e., no post-selection of any kind. The initial states are defined by a set of vectors
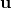
, each one of which is accounted for in the calculation of the correlations.
They say there is no point in flogging a dead horse, but Bell's theorem seems to be an exception. It needs to be obliterated from the consciousness of the community.
I want to bring out something that usually gets obscured in the discussions about the so-called Bell's theorem (we shall not be concerned about trivial variants of such "theorems" by lesser brains---the proponents of such trivialities are advised to promote their nonsense elsewhere).
The dying breed of the Bell mafia (when they are not engaged in spreading despicable violence and terror) routinely demand things from their chastisers that are [b][i][u]not[/u][/i][/b] predicted by quantum mechanics, since they have been systematically deprived of valid predictions of quantum mechanics they can pretend to play their game with.
Take, for example, the familiar predictions of the four pairs of Bell-test angles in an EPRB-type experiment:
[tex]{\rm E}(0, 45) = - 0.7071...,[/tex]
[tex]{\rm E}(0, 135) = + 0.7071...,[/tex]
[tex]{\rm E}(90, 45) = - 0.7071...,[/tex]
[tex]{\rm E}(90, 135) = - 0.7071....[/tex]
On the face of it there seem to be nothing wrong with these predictions. The expectation value of the products of measurement results when Alice has her polarizer oriented at 0 degrees and Bob has his polarizer oriented at 45 degreees is -0.7071..., and the expectation value of the products of measurement results when Alice has her polarizer oriented at 0 degrees and Bob has his polarizer oriented at 135 degreees is +0.7071..., and so on. But look closely and you will find that this is not really what quantum mechanics actually predicts. If we call Alice's polarization angle [tex]\alpha[/tex] and Bob's polarization angle [tex]\beta[/tex], then quantum mechanics actually predicts
[tex]{\rm{E}}_{\rm QM}(\alpha - \beta)=\langle\Psi|\,\widehat{O}({\alpha},\,{\beta})|\Psi\rangle=-\cos(\alpha - \beta)[/tex]
where [tex]|\Psi\rangle[/tex] is the singlet state. In other words, quantum mechanics neither knows nor predicts anything about the [b][i][u]absolute[/u][/i][/b] polarization angles [tex]\alpha[/tex] and [tex]\beta[/tex]. To be sure experimenters are free to choose them as they will, but quantum mechanics couldn't care less about them. It only cares (i.e., makes predictions) about quantities dependent on the [b][i][u]relative[/u][/i][/b] angle [tex](\alpha - \beta)[/tex] between the polarization directions. Thus the above stated four quantitative predictions are actually an overstatement of the facts. The valid predictions of quantum mechanics are only the following two predictions, reducing the above four to two:
[tex]{\rm E}[(\alpha - \beta) = 45] = - 0.7071...,[/tex]
[tex]{\rm E}[(\alpha - \beta) = 135] = + 0.7071....[/tex]
This effectively means that, without violating any predictions of quantum mechanics, we can always set one of the polarization angles to zero and measure the variations in the correlation with respect to that setting. This does not compromise the free will of the experimenter. It only sets a convention for a coordinate system. Thus, for definiteness, we can either set [tex]\beta = 0[/tex] or set [tex]\alpha = 0[/tex]. In the following simulation I show the correlations these two possible conventions lead to:
http://rpubs.com/jjc/16415.
Let me stress again: To demand control over [b][i]absolute[/i][/b] values of [tex]\alpha[/tex] and [tex]\beta[/tex] in this simulation is to demand something beyond the confines of quantum mechanics, even if experimenters may have such a control. Thus when the Bell mafia make such demands they are as usual being themselves---i.e., being sore losers and dishonest.
Moreover, it is important to note that in the above simulation there is no filter of any kind---i.e., no post-selection of any kind. The initial states are defined by a set of vectors [tex]{\bf u}[/tex], each one of which is accounted for in the calculation of the correlations.
They say there is no point in flogging a dead horse, but Bell's theorem seems to be an exception. It needs to be obliterated from the consciousness of the community.
