A new, simplified derivation of the EPR-Bohm correlation

[Joy Christian]

***
Hi Everyone,

I have produced a new, simplified, local-realistic derivation of the EPR-Bohm correlation that may be of interest:

https://www.academia.edu/16328957/A_sim ... orrelation

The novelty here is that I have avoided using the concept of standard scores, which has been a stumbling block for some.

I now calculate the correlation E(a, b) = -a.b directly using the raw scores A = +/-1 and B = +/-1, albeit still within S^3.

[FrediFizzx]

***
Hi Everyone,

I have produced a new, simplified, local-realistic derivation of the EPR-Bohm correlation that may be of interest:

https://www.academia.edu/16328957/A_sim ... orrelation

The novelty here is that I have avoided using the concept of standard scores, which has been a stumbling block for some.

I now calculate the correlation E(a, b) = -a.b directly using the raw scores A = +/-1 and B = +/-1, albeit still within S^3.

Bravo! Much cleaner. However, shouldn't eq. (3) technically be,

L(n, l) = l D(n) <--> D(n) = l L(n, l)

where I have used l for lambda and n is either a or b?

[Joy Christian]

***
Hi Everyone,

I have produced a new, simplified, local-realistic derivation of the EPR-Bohm correlation that may be of interest:

https://www.academia.edu/16328957/A_sim ... orrelation

The novelty here is that I have avoided using the concept of standard scores, which has been a stumbling block for some.

I now calculate the correlation E(a, b) = -a.b directly using the raw scores A = +/-1 and B = +/-1, albeit still within S^3.

Bravo! Much cleaner. However, shouldn't eq. (3) technically be,

L(n, l) = l D(n) <--> D(n) = l L(n, l)

where I have used l for lambda and n is either a or b?

Sure. Perhaps it is better to use a generic vector n, but it does not really mater. The vector "a" is supposed to span all directions as usual (Bell, for example, never uses n to indicate a generic vector --- he just writes "a" or "b" as generic vectors spanning all space). But it is easy to update the paper, so I will do so.

PS: The Academia.edu website sucks. It does not let me edit the paper for some reason. I often have problems with that website. It does not match their ambition.

[FrediFizzx]

Sure. Perhaps it is better to use a generic vector n, but it does not really mater. The vector "a" is supposed to span all directions as usual (Bell, for example, never uses n to indicate a generic vector --- he just writes "a" or "b" as generic vectors spanning all space). But it is easy to update the paper, so I will do so.

PS: The Academia.edu website sucks. It does not let me edit the paper for some reason. I often have problems with that website. It does not match their ambition.

Well, it is edited now. Looks perfect. Now..., before Lockyer and Reed (or any others) come along and want to mangle eq. (11) and cause confusion, here is some further explanation about it that I posted on Albert Jan's blog.

For a pair of particles that are in a singlet configuration, Nature has a 50-50 chance that they will be created as either a left handed system or right handed system. And that is just plain common sense. For a left handed system the expression is;

(I.a)(I.b) = -a.b - (a^b) = -a.b - I.(a x b) (1) LH System

For the right handed system we have;

(I.a)(I.b) = -a.b - (a^b) = -a.b - I.(a x b) (2) RH System

Note that both equations are the same. However, eq. (1) is in a left handed basis and eq. (2) is in a right hand basis so we can't add the left hand expression to the right hand expression properly. Now, translate eq. (1) to the right hand basis so that we can do that.

But first I want to stress, "However, eq. (1) is in a left handed basis and eq. (2) is in a right hand basis so we can't add the left hand expression to the right hand expression properly." The translation of eq. (1) to the right hand basis is simply;

(I.b)(I.a) = (-I.a)(-I.b) = -a.b - (-I).(a x b) = -a.b + a^b

GAViewer cofirms that this is correct.

>> -a.b + a^b
ans = 0.77 + 0.39*e2^e3 + -0.44*e3^e1 + -0.25*e1^e2
>> (I.b)*(I.a)
ans = 0.77 + 0.39*e2^e3 + -0.44*e3^e1 + -0.25*e1^e2

So that further explains eq.(11) and eq. (12) easily follows from that combined with eq. (10).

[FrediFizzx]

***
Hi Everyone,

I have produced a new, simplified, local-realistic derivation of the EPR-Bohm correlation that may be of interest:

https://www.academia.edu/16328957/A_sim ... orrelation

The novelty here is that I have avoided using the concept of standard scores, which has been a stumbling block for some.

I now calculate the correlation E(a, b) = -a.b directly using the raw scores A = +/-1 and B = +/-1, albeit still within S^3.

And here is GAViewer confirmation of eq. (8).

Code: Select all

//Adaptation of Albert Jan Wonnink's original code
//http://challengingbell.blogspot.com/2015/03/numerical-validation-of-vanishing-of.html

function getRandomLambda()
{
     if( rand()>0.5) {return 1;} else {return -1;}
}

function getRandomUnitVector() //uniform random unit vector:
   //http://mathworld.wolfram.com/SpherePointPicking.html
{
     v=randGaussStd()*e1+randGaussStd()*e2+randGaussStd()*e3;
     return normalize(v);
}

batch test()
{
     set_window_title("Test Joy Christian's S^3 Model");
     N=20000; //number of iterations
     I=e1^e2^e3;
     s=0;

     a=getRandomUnitVector();
     b=getRandomUnitVector();

     minus_cos_a_b=-1*(a.b);

     for(nn=0;nn<N;nn=nn+1) //perform the experiment N times
     {
          lambda=getRandomLambda(); //lambda is a fair coin,
                 //resulting in +1 or -1
          mu=lambda*I;
          La=mu.a;
          Lb=mu.b;
          q=0;
          if(lambda==1) {q=(-La) Lb Lb Lb;} else {q=Lb Lb Lb (-La);}
          s=s+q; //summation of all terms.
}
     mean_mu_a_mu_b=s/N;
     print(mean_mu_a_mu_b, "f"); //print the result
     print(minus_cos_a_b, "f");
     prompt();

}

Typical results are;

mean_mu_a_mu_b = -0.704397 + 0.006960*e2^e3 + -0.001450*e3^e1 + 0.002672*e1^e2
minus_cos_a_b = -0.704397

And GAViewer confirmation of eq. (12);

>> Eab=((I.a)(I.b)+(I.b)(I.a))/2
>> print(Eab, "f")
Eab = -0.704397

[Joy Christian]

***
Hi Everyone,

I have produced a new, simplified, local-realistic derivation of the EPR-Bohm correlation that may be of interest:

https://www.academia.edu/16328957/A_sim ... orrelation

The novelty here is that I have avoided using the concept of standard scores, which has been a stumbling block for some.

I now calculate the correlation E(a, b) = -a.b directly using the raw scores A = +/-1 and B = +/-1, albeit still within S^3.

For any future reference, I also have a DOI number for this publication: DOI: 10.13140/RG.2.1.3482.1847

[Joy Christian]

I have revised the paper slightly (very slightly): https://www.academia.edu/16328957/A_sim ... orrelation

[Joy Christian]

***
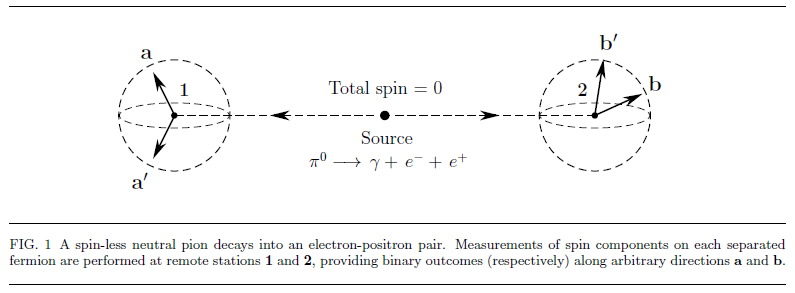
Here is an instructive picture of the EPR-Bohm experiment discussed in the above paper --- it has been reproduced from this paper:

[Joy Christian]

***
The paper is now also on the arXiv: http://arxiv.org/abs/1103.1879 , as version 2 of my "Disproof of Bell's Theorem" paper.
***

[FrediFizzx]

***
The paper is now also on the arXiv: http://arxiv.org/abs/1103.1879 , as version 2 of my "Disproof of Bell's Theorem" paper.
***

I like it! This new version is absolutely irrefutable. As VP Joe Biden would say, "This is a big freakin' deal!". I smell a revolution in physics coming.

[Joy Christian]

***
The paper is now also on the arXiv: http://arxiv.org/abs/1103.1879 , as version 2 of my "Disproof of Bell's Theorem" paper.
***

I like it! This new version is absolutely irrefutable. As VP Joe Biden would say, "This is a big freakin' deal!". I smell a revolution in physics coming.

[Joy Christian]

After eight years of bogus criticisms of my model, online harassments, cyber-stalking, lying, cheating, and malicious letters writing, Richard Gill has finally admitted that my model does predict the strong correlation < AB > = -a.b, with A = +/-1 and B = +/-1. His admission reminds me of Tony Blair's recent apology for the Iraq war.

[Heinera]

You should delete your post alluding to a "violent revolution". It makes one wonder about your plan of further actions.

[FrediFizzx]

You should delete your post alluding to a "violent revolution". It makes one wonder about your plan of further actions.

I suspect it is a form of British humour. Get over it.
https://en.wikipedia.org/wiki/British_humour

[jreed]

:o

After eight years of bogus criticisms of my model, online harassments, cyber-stalking, lying, cheating, and malicious letters writing, Richard Gill has finally admitted that my model does predict the strong correlation < AB > = -a.b, with A = +/-1 and B = +/-1. His admission reminds me of Tony Blair's recent apology for the Iraq war.

Joy, please give me a reference where Richard admits that your expression < AB > = -a.b is correct. I can't find that anywhere.

[Joy Christian]

Joy, please give me a reference where Richard admits that your expression < AB > = -a.b is correct. I can't find that anywhere.

I am not honouring any of your requests. You lost that right long ago.

[jreed]

Joy, please give me a reference where Richard admits that your expression < AB > = -a.b is correct. I can't find that anywhere.

I am not honouring any of your requests. You lost that right long ago.

Then I'll just have to assume that my first thought about your statement was right. That was that he would never agree that you were correct. Looking at your paper I can't understand how anyone would believe that it makes sense.

[Joy Christian]

Looking at your paper I can't understand how anyone would believe that it makes sense.

My paper is not written for anyone who believes that factoring out zero is a legitimate mathematical operation: viewtopic.php?f=6&t=199&start=40#p5582

***
The paper is now also on the arXiv: http://arxiv.org/abs/1103.1879 , as version 2 of my "Disproof of Bell's Theorem" paper.
***

I like it! This new version is absolutely irrefutable. As VP Joe Biden would say, "This is a big freakin' deal!". I smell a revolution in physics coming.

[Joy Christian]

***

It is worth noting here that, in the context of the equations (5) and (6) of the above paper, the following more general identity of limits also holds:



It is quite easy to verify this identity of limits. Alternatively, one can just look up the general properties of limits in a good schoolbook on calculus.

***

[FrediFizzx]

***

It is worth noting here that, in the context of the equations (5) and (6) of the above paper, the following more general identity of limits also holds:



It is quite easy to verify this identity of limits. Alternatively, one can just look up the general properties of limits in a good schoolbook on calculus.

***

Perhaps the notation you are using on the RHS might be messing up some people? I think usually it is something like s --> (a', b') or would it be (s, s) --> (a', b')?
http://tutorial.math.lamar.edu/Classes/ ... imits.aspx

Anyways, it is perfectly understandable what you are doing either way.