Justo wrote:)
is the mean of a long series of joint measurements by Alice and Bob with setting a_i and b_k, each made on different entangled particles generated on the same event.
Freedom means that
=\rho(\lambda))
, if you do not assume that, the derivation cannot go through. It should be very simple and obvious.
I don't think you got the point. There are only 4 expectation values that are measured in the Bell-test experiment. When Alice and Bob measure
)
. The settings are constant, and their average is a constant for which QM has a specific prediction of
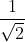
As we already agreed, each of those expectation values is obtained from a different set of particle pairs in the singlet state. Therefore there is nothing about one set that influences the other set in any way. The only requirement is that each set of pairs is in the singlet state. Therefore the freedom of Alice and Bob is irrelevant for the expectation value
)
and
=\rho(\lambda))
is completely superfluous. Perhaps what you are calling freedom is not really freedom because it has nothing to do with the freedom of Alice and Bob. Maybe I should ask you the question another way:
Alice and Bob's freedom to do what? Certainly not in picking settings because the settings are constant as already explained.
So what do you mean by freedom? Let us explore that question by continuing with Justo's paper
https://arxiv.org/pdf/1911.00343.pdf, let's look at equation (8).
 = A(a_1, \lambda)B(b_1, \lambda) - A(a_1, \lambda)B(b_2, \lambda) + A(a_2, \lambda)B(b_1, \lambda) + A(a_2, \lambda)B(b_2, \lambda))
First, this expression is misleading as the settings are constants so I will simplify as follows without any loss of meaning,
 = A_1(\lambda)B_1(\lambda) - A_1(\lambda)B_2(\lambda) + A_2(\lambda)B_1(\lambda) + A_2(\lambda)B_2(\lambda))
But there is another problem with this expression: We mentioned that the expression pertains to 4 different sets of particle pairs. Therefore this should be corrected as follows:
 = A_1(\lambda_w)B_1(\lambda_w) - A_1(\lambda_x)B_2(\lambda_x) + A_2(\lambda_y)B_1(\lambda_y) + A_2(\lambda_z)B_2(\lambda_z))
With the above clarification, the expression now correctly captures the mathematics of the Bell test experiments which Justo's equation 8 did not. This is the proper starting point for doing any derivation of any Bell inequality. It is very easy to make hidden assumptions by using sloppy notation and Bell did plenty of that.
Note that
)
is an expression in which we are doing arithmetic with functions, not plain numbers. And there is a very important mathematical restriction that applies when we do this type of arithmetic:
1.
)
is only defined for the common part of the domain of all the functions. That is, it is only defined for

(see Gill & Larsson for an alternative a treatment of this point) . Given that

are random variables it is unlikely that they will be the same but let us grant that for a very large number of measurements they will almost be the same. This assumption has nothing to do with freedom. It is an assumption of fair sampling.
2. Let me burst the bubble of anyone who was tempted to think that the above assumption resolves all the problems. There is a bigger problem.
We don't just have the addition of functions above, we have the addition of products of functions which we eventually factorize! This means not only do the domains have to match, but the ordering also has to match too (
 \cdot f(x) = (f\cdot g)(x))
). You can visualize it by considering each function as a 2xN spreadsheet where column 1 contains the elements of the domain of the function
and column 2 contains the corresponding output of the function (the images).
The factorization
 = A_1(\lambda_w)[B_1(\lambda_w) -B_2(\lambda_x)] + A_2(\lambda_y)[B_1(\lambda_y) + B_2(\lambda_z)])
involves an implicit assumption that
 \equiv A_1(\lambda_w))
, which means the rows of the two spreadsheets
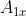
and
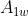
have to be rearranged so that the columns 1 & columns 2 are practically identical between the two spreadsheets. But note that the second requirement above means that Column 1 on spreadsheet
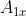
must always match Column 1 on spreadsheet

. Therefore any permutations we apply to
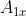
must also be applied to

for the above factorization to be permissible.
The same thing applies to the second factorization where we imply that
 \equiv A_2(\lambda_z))
. Now, to complete the derivation, 2 additional assumptions are required, that
 \equiv B_1(\lambda_y))
and also that
 \equiv B_2(\lambda_z))
. In each of these assumptions, the same requirements for being able to rearrange the spreadsheets applies. But we immediately run into problems. We can't rearrange

without breaking the earlier requirement since we already rearranged it when we tried to make
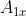
agree with
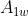
. Any changes will disrupt the agreement and forbid factorization. Same thing applies to
)
.
Again it is very important to note that the fair sampling assumption (which we've granted in restriction 1, only says the probability distribution of values in Column 1 is the same for all the 8 spreadsheets. It says nothing about the ordering of those values. Therefore the Fair sampling assumption does nothing to resolve the real problem. Secondly, you will notice that freedom is not involved in this discussion. Again I ask: Freedom to do what?
Let us pretend that what I just demonstrated was not the case. Let us pretend that as soon as the first two permutations are done, then all the pairs of spreadsheets that need to be rearranged will automatically match and we won't have any problems. I'm sure there are those who believe such a ridiculous idea but for the sake of argument, let us evaluate it for a moment. It would mean that at the end of the day, there are effectively only 4 2xN spreadsheets with identical Column 1 on all the spreadsheets. In other words, it would mean that there are only 4 functions
, B(b_1, \lambda), A(a_2, \lambda), B(b_2, \lambda))
with exactly the same domain in the experiments. And it would mean, the four Column 2s can be combined into a single 4xN spreadsheet of outcomes. Now, where have we seen a 4xN spreadsheet of outcomes? Oh, that's my scenarios 3 & 4 which Justo calls "tautological" and meaningless.
So there is no escape, the conclusion is obvious:
- The mathematical operations involved in the derivation of Bell's inequality make assumptions that are false.
- But even if we grant that those assumptions aren't false, the assumptions imply that the data can be combined into a 4xN spreadsheet, a scenario for which QM does not predict a violation.
- Freedom to do what?


