A simple two-page proof of local realism

[FrediFizzx]

OK, we are done. I have revised my simulation: http://rpubs.com/chenopodium/13653.

Let me remind again that the initial state of the system is still (e_o, theta_o), as derived in http://libertesphilosophica.info/blog/w ... mplete.pdf, but the choice of the initial function f(theta_o) is now different:

f(theta_o) = (1/2.47) sin(theta_o)^{1.61}.

That makes me highly suspect that something is not right with the R program and/or the R programming.
...

[gill1109]

The problem is that we have no mathematical derivation of the function f. We are just guessing. And tuning our guesses by numerical search.

Maybe you can get a better guess using Mathematica, Fred. You paid good money for it, let us see you put it through its paces!

Notice that I managed to reduce the error from 0.02 to 0.002 by a day of creative R work and an inspired guess or two.

OK, we are done. I have revised my simulation: http://rpubs.com/chenopodium/13653.

Let me remind again that the initial state of the system is still (e_o, theta_o), as derived in http://libertesphilosophica.info/blog/w ... mplete.pdf, but the choice of the initial function f(theta_o) is now different:

f(theta_o) = (1/2.47) sin(theta_o)^{1.61}.

That makes me highly suspect that something is not right with the R program and/or the R programming.
...

[FrediFizzx]

Mathematica says that Joy's original function 0.5 sin^2(theta) with theta (0,pi/2) is the best for f. Those slight deviations around the peaks will be gone when trials go to infinity and degree increments go to 0. No big deal. There is either something wrong with the R programming or R is a piece of junk.

I'm still waiting for you to prove what I am saying is false. Figured that you can't do it because you know it is in fact a waste of time because what I am claiming is true.

[gill1109]

My proof is statistical, and computational, not analytic. It consists of comparing the difference between the two curves to the standard error of the Monte Carlo curve ...

We must be sure that we have removed all sources of systematic error (bias) from the simulation, and we must of course take account of the numerical precision of our computing environment.

The computational / statistical proof that you are wrong is a whole lot stronger than the statistical proof for the existence of the Higgs Boson.

There is nothing wrong with Mathematica but quite a lot wrong with the implementation of the simulation model which you are using. Quite a lot of opportunities to reduce systematic error.

Everyone else I know who is interested in this simulation business, is busy improving their code, and generally speaking, adopting my refinements: Daniel Sabsay, John Reed, Chantal Roth...

Joy and Chantal have adopted improvements which I made in Michel Fodje's simulation.

If you think that your plot together with some calculus proves anything ... well I am too polite to say here what I think about that.

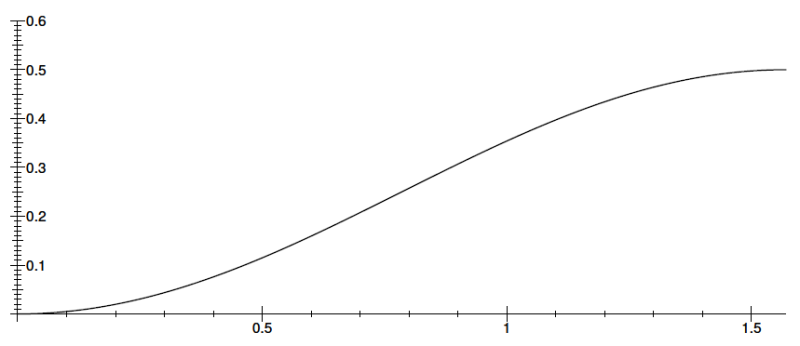
[Joy Christian]

Mathematica says that Joy's original function 0.5 sin^2(theta) with theta (0,pi/2) is the best for f. Those slight deviations around the peaks will be gone when trials go to infinity and degree increments go to 0. No big deal. There is either something wrong with the R programming or R is a piece of junk.

I'm still waiting for you to prove what I am saying is false. Figured that you can't do it because you know it is in fact a waste of time because what I am claiming is true.

I am indeed becoming increasingly curious about your claim. Although the anecdotal evidence seems to favor the R-based claim that the function 0.5 sin^2(theta) with theta in [0, pi/2] is not exactly true at greater precision, all of this anecdotal evidence is based on finite number of trials and finite degree of increments. But as we know, my analytical model is based on a smooth, simply-connected manifold S^3. So your argument, after all, may win the day in the end. We need more evidence.

[gill1109]

Mathematica says that Joy's original function 0.5 sin^2(theta) with theta (0,pi/2) is the best for f. Those slight deviations around the peaks will be gone when trials go to infinity and degree increments go to 0. No big deal. There is either something wrong with the R programming or R is a piece of junk.

I'm still waiting for you to prove what I am saying is false. Figured that you can't do it because you know it is in fact a waste of time because what I am claiming is true.

I am indeed becoming increasingly curious about your claim. Although the anecdotal evidence seems to favor the R-based claim that the function 0.5 sin^2(theta) with theta in [0, pi/2] is not exactly true at greater precision, all of this anecdotal evidence is based on finite number of trials and finite degree of increments. But as we know, my analytical model is based on a smooth, simply-connected manifold S^3. So your argument, after all, may win the day in the end. We need more evidence.

The "finite degree of the increments" is not an issue here. We can talk about the values of some particular curves, at some particular values.

If I may use the language of probability theory, the "0.5 sin^2(theta)" simulation model is:

Take two points a, b in S^2 with a.b = cos(phi)
Let Theta ~ Uniform([0, pi/2])
Let E ~ Uniform(S^2), independent of Theta.

Define A = sign(a.E) if abs(a.E) > sin( 0.5 sin^2(Theta) ) otherwise 0
Define B = sign(b.E) if abs(b.E) > sin( 0.5 sin^2(Theta) ) otherwise 0

Define rho(a, b) = E( AB | AB != 0)

Simulation experiment. Pick any a, b (anyway you like), suppose a.b = cos(phi). Keep them fixed.

M times, independenly of one another, pick Theta and E as described above. (I'm keeping a and b fixed, all the time).
Each time, define A and B as above and report the average of the products of A times B, divided by the number of times A times B was unequal to zero. Call this "rhoHat", the estimated correlation. Let N = number of times that AB was unequal to zero.

Elementary statistics tells me that rhoHat is an unbiased estimator of rho(a, b) and that, conditional on N=n, its variance is less than 1/n.

Basically we have a binomial experiment: given N=n, N(++) + N(--) has the binomial distribution with parameters n and p, where p = (rho + 1)/2 and equivalently rho = 2 p - 1. And, rhoHat= 2 pHat -1 with pHat = (N(++) + N(--))/n.

The question we are interested in, is: "Is rho(a, b), as defined above, equal to cos(phi)"?

The numerical accuracy of R, Mathematica, Python is about 10^-17 if I remember correctly (floating point real arithmetic, i.e. "double precision" real numbers represented by two 32 bit words). All of these systems have excellent pseudo random number generators. I am sure they can all compute cosine and sine functions to sufficient accuracy for our present purposes.

The important thing to notice is that there is no binning of continuous angles here, at all! Generating angles a and b at random, uniformly on 0 2 pi, might correspond to some kinds of real experiments, but even experimenters know that they can also "do the experiment" with the settings fixed for a long time. If all settings are different because each new one is random and uniform, then we have to bin or smooth in some way to get curves. But I want to determine just one point on the curve as accurately as possible. Or just a few points on the curve. It's sufficient for present purposes.

[Joy Christian]

But I want to determine just one point on the curve as accurately as possible. Or just a few points on the curve. It's sufficient for present purposes.

That is not sufficient to test my model. The smooth and simply-connected topology of S^3 predicts what will be observed at one point, but not the other way around.

[Joy Christian]

OK, we are done. I have revised my simulation: http://rpubs.com/chenopodium/13653.

Let me remind again that the initial state of the system is still (e_o, theta_o), as derived in http://libertesphilosophica.info/blog/w ... mplete.pdf, but the choice of the initial function f(theta_o) is now different:

f(theta_o) = (1/2.47) sin(theta_o)^{1.61}.

It is also important to note that the Monte Carlo accuracy of the simulation is about 0.0001, but any remaining wrinkles in the correlation function are much smaller than 0.0001.

Here is how the initial function f(theta_o) looks like in a pictorial form (the degrees on the x-axis are in radians):

[img]http://libertesphilosophica.info/blog/wp-content/uploads/2014/02/ft_o-e1393521103933.pn

It appears that changing the interval of theta_o from [0, pi/2] to something else would affect the correlation significantly.

And for comparision, here is the original initial function f(theta_o) = (1/2) sin(theta_o)^{2} used in Michel's simulation:

[gill1109]

It appears that changing the interval of theta_o from [0, pi/2] to something else would affect the correlation significantly.

Sure. And changing the distribution of theta_0 from uniform, to something else, would change it too. What finally counts is not the whole triple: the function f, and the interval for theta_0, and the distribution for theta_0; but only the probability distribution of the finally result - the thing that you compare with the absolute value of the cosine of the angle between e_0 and a, and similarly e_0 and b: sin(f(theta_0)).

I defined R by cos(R) = sin(f(theta_0)) and looked at different probability distributions for R, temporarily forgetting all the other objects. That way, I found a better fit to the result we are looking for: a.b

But still not exact. But I am pretty sure that there is a an exact solution to this purely mathematical question ... only it might not have a nice analytic expression. I think I can prove that the exact solution does indeed exist, and I think I can compute it to arbitrarily high accuracy. But for higher accuracy that 0.0001 or so we should forget about Monte Carlo. There are analytical formulas for the probabilities coming out of Caroline Thompson's model, and as I tried to explain, there is a mathematical isomorphism between the abstract objects in a simulation of her model and in your simulation of your model.

[Joy Christian]

OK, we are done. I have revised my simulation: http://rpubs.com/chenopodium/13653.

Let me remind again that the initial state of the system is still (e_o, theta_o), as derived in http://libertesphilosophica.info/blog/w ... mplete.pdf, but the choice of the initial function f(theta_o) is now different:

f(theta_o) = (1/2.47) sin(theta_o)^{1.61}.

It is also important to note that the Monte Carlo accuracy of the simulation is about 0.0001, but any remaining wrinkles in the correlation function are much smaller than 0.0001.

Here is how the initial function f(theta_o) looks like in a pictorial form (the degrees on the x-axis are in radians):



It appears that changing the interval of theta_o from [0, pi/2] to something else would affect the correlation significantly.

And for comparision, here is the original initial function f(theta_o) = (1/2) sin(theta_o)^{2} used in Michel's simulation:

PS: I messed-up one of the plots above, so here they are again, both now corrected.

[Joy Christian]

Take two points a, b in S^2 with a.b = cos(phi)
Let Theta ~ Uniform([0, pi/2])
Let E ~ Uniform(S^2), independent of Theta.

Define A = sign(a.E) if abs(a.E) > sin( 0.5 sin^2(Theta) ) otherwise 0
Define B = sign(b.E) if abs(b.E) > sin( 0.5 sin^2(Theta) ) otherwise 0

Define rho(a, b) = E( AB | AB != 0)

RIght. But how do _y_o_u_ interpret this, Richard? In my opinion, there are only two options:

1. There is a probability (depending on the directions defined by a and b) that some particles are not detected (the "0" outcomes) at both detectors, and this probability of nondetection gives us the right correlation. Well, this is clear one kind of detection loophole. Something that I don't consider plausible.

2. The distribution of (E,Theta) depends on the unity vectors a and b. Hence, particles with a hidden state such that, for instance, abs(a.E) <= sin( 0.5 sin^2(Theta) ) do not exist (with probability one). This is blatantly non-local.

Your two options are ambiguous without specifying how you are modelling the physical space itself. If you are modelling it as R^3, then what you are saying is true. But if you are modelling it as S^3---which is one of the three possible solutions of Einstein's field equations (an FRW solution)---then what you are saying is not true.

[FrediFizzx]

I am indeed becoming increasingly curious about your claim. Although the anecdotal evidence seems to favor the R-based claim that the function 0.5 sin^2(theta) with theta in [0, pi/2] is not exactly true at greater precision, all of this anecdotal evidence is based on finite number of trials and finite degree of increments. But as we know, my analytical model is based on a smooth, simply-connected manifold S^3. So your argument, after all, may win the day in the end. We need more evidence.

That is exactly right and never fear... Fred is here! Anyone that knows calculus can easily see what is going on here. The peaks of the curve are the hardest parts of the curve to cover and you need a billion jillion trials and very small degree increments to get that part of the curve "filled in" accurately. You know all the stuff we tried adjusting the f function on Mathematica don't even come close to working very well so that makes me think there is either something wrong with the R programming or R has some flaws itself. I certainly trust Mathematica a whole lot more since millions and millions of people use it every day in all sorts of fields.

[gill1109]

you need a billion jillion trials and very small degree increments to get that part of the curve "filled in" accurately.

I am not talking about "filling in the curve". I am interested in computing just one point on it. Say, the value of the curve at 15 degrees. For that purpose, 100 million trials with alpha = 15 degrees and beta = 0 will tell you the answer to accuracy 0.0001. Mathematica will do the job fine, so will R, so will Python. I want one number, not a pretty graph.

[gill1109]

RIght. But how do _y_o_u_ interpret this, Richard? In my opinion, there are only two options:

1. There is a probability (depending on the directions defined by a and b) that some particles are not detected (the "0" outcomes) at both detectors, and this probability of nondetection gives us the right correlation. Well, this is clear one kind of detection loophole. Something that I don't consider plausible.

2. The distribution of (E,Theta) depends on the unity vectors a and b. Hence, particles with a hidden state such that, for instance, abs(a.E) <= sin( 0.5 sin^2(Theta) ) do not exist (with probability one). This is blatantly non-local.

Both 1 and 2 are feasible interpretations. Caroline Thompson adhered to 1), and associated it with the detection loophole. She found evidence from Aspect's data supporting that: the pair detection rate depends on the difference between the two angles. 2) would correspond to the conspiracy loophole: both settings are known in advance by both detectors since both caused by events in intersection of their past light cones.

Joy has a third interpretation but I don't understand his maths.

[gill1109]

Just been checking some classic references from

http://freespace.virgin.net/ch.thompson ... Record.htm

Apparently Caroline didn't realise it herself, but her "unsharp" chaotic rotating ball had at least two precursors:

Pearle, P, “Hidden-Variable Example Based upon Data Rejection”, Phys. Rev. D 2, 1418-25 (1970).

T. W. Marshall, E. Santos and F. Selleri: “Local Realism has not been Refuted by Atomic-Cascade Experiments”, Phys. Lett. A 98, 5-9 (1983).

Using the isomorphism between the generalized 3-D Minkwe simulation model (generalized to allow an arbitrary probability distribution of S = sin(f(theta_0)) and the generalized chaotic ball models (the radius R of the circular caps becomes random, R = arc cos(S)), one can use Pearle (1970) to deduce the *unique* probability distribution of S = sin(f(theta_0)) = cos(R) which will reproduce *exactly* the cosine. So here is mathematical proof that all choices dreamt up to date are actually off target, since they are clearly not quite identical to Pearle's solution.

Marshall et al. essentially give us a numerical procedure to determine the probability distribution of f(theta_0) to any desired degree of accuracy, using Fourier theory, but apparently they did not realise that Pearle had got an exact analytical solution. For many years his paper was considered too difficult for anyone to read. So his result got re-discovered time and time again.

[Joy Christian]

OK, now we are well and truly done. I have revised my simulation again: http://rpubs.com/chenopodium/joychristian.

The initial state of the system (e_o, theta_o) is derived in http://libertesphilosophica.info/blog/w ... mplete.pdf, and the choice of the initial function f(theta_o) is

f(theta_o) = (1/2) sin^2(theta_o).

What is different in this version is the range of theta_o. This time any remaining wrinkles in the correlation are indeed well within the accuracy of the simulation.

[gill1109]

Congratulaions! Very nice!

At N = 10^7, the difference between the cosine and the curve which you are effectively computing by Monte-Carlo is smaller than the Monte-Carlo error (of order 1 / sqrt N) inherent in sample size of N = 10^7.

We are slowly converging towards Pearle's (1970) solution. If we would increase N further still, we would see small systematic errors again; but we could fix them again - for the time being - by introducing further new parameters (a little more flexibility in the description of f or of the distribution of theta_0 or whatever). And so on ad infinitum. The solution will converge to Pearle's solution. It must do so, because we know that a solution exists and is unique. Pearle described it analytically.

[Joy Christian]

Congratulaions! Very nice!

Thank you, Richard. There is a lot more room in the range of theta_o. So, sure, one can keep on going to higher and higher level of accuracy and precision.

This version will please Fred too, because it retains the original choice of the function f(theta_o), with its geometrical connection to S^3 and Chantal's original simulation intact. The peculiar range of theta_o in this version can be understood as well, but I don't have the full argument worked out as yet.

[FrediFizzx]

OK, now we are well and truly done. I have revised my simulation again: http://rpubs.com/chenopodium/joychristian.

The initial state of the system (e_o, theta_o) is derived in http://libertesphilosophica.info/blog/w ... mplete.pdf, and the choice of the initial function f(theta_o) is

f(theta_o) = (1/2) sin^2(theta_o).

What is different in this version is the range of theta_o. This time any remaining wrinkles in the correlation are indeed well within the accuracy of the simulation.

I ran it in Mathematica with those parameters, 5 million trials. It's still off. The straighter part of the curve is not coming in now.

[Joy Christian]

I ran it in Mathematica with those parameters, 5 million trials. It's still off. The straighter part of the curve is not coming in now.

Thanks, Fred. I am glad you anticipated my request and ran it through Mathematica already. So now we have another puzzle to solve. I am also curious to know whether it will work in Python. We will ask Michel to check it out.