This thread is depressing. A lot of bickering and talking past each other. A lot of unwarranted abuse heaped on Gordon for concepts that are not controversial.
In Bell's derivation. The
)
is simply the expectation value for the paired-product of the outcomes an EPR experiment with Alice setting

and Bob's setting
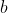
, where the outcomes at Alice and Bob are represented mathematically as

. An expectation value is a generalization of a weighted average calculated over any valid probability space of the experiment.
It is easy to envision three probability spaces:
1. The one used by Bell, which divides the outcomes based on outcomes
 = \pm 1, B_b(\lambda) = \pm 1)
hidden variables

and corresponding probability functions
)
, where
d\lambda = 1)
resulting in the expectation value:
 A_a(\lambda)B_b(\lambda)d\lambda)
Note: I've fixed two notational problems in Bell's original paper: (1) The symbols

and
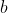
are labels, not variables since their values do not change during the experiment (2). I've used
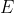
instead of
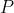
to denote expectation, which is more standard.
2. An alternative probability space, defined over the actual outcome pairs obtained
,(-1,-1),(+1,-1),(-1,+1) \})
and the corresponding probabilities
)
where
d\phi = P(A_a^+B_b^+) + P(A_a^-B_b^-) + P(A_a^+B_b^-) + P(A_a^-B_b^+) = 1)
. This yields the expectation of the paired product as:
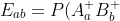A_a^+B_b^+ + P(A_a^-B_b^-)A_a^-B_b^- + P(A_a^+B_b^-)A_a^+B_b^- + P(A_a^-B_b^+)A_a^-B_b^+)
 + P(A_a^-B_b^-) - P(A_a^+B_b^-) - P(A_a^-B_b^+))
Which is essentially Gordon's equation 5.
I fail to see the relevance of the discussion about the production of two functions to what is described in the 2-page paper linked above. Perhaps there could be some discussion about the relevance of invoking Malus law but the math up to at least equation 7 appears very valid.

