FrediFizzx wrote:Here is what Gull's number (3) looks like to me,
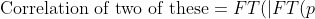|^2) (mp2))
If that is correct, please define FT(p) and (mp2). Please don't add a bunch of rambling nonsense. And..., it looks like to me that Correlation of two of these will equal 0 or +1.
.
(MP2) is a reference. Computer programming project, second part of specs. (MP = maths project?)
First part is the stuff about separate computers, the two synchronized dialogues, no use of past inputs and no communication; second partis that we must create the cosine function.
You know of course that the inverse Fourier transform is the Fouriert ransform itself? (If you define it the right way so that it’s normalised - it’s an L2 isometric, and it’s idempotent, in fancy words). So he could also have written (but he forgot the minus sign)
FT(correlation) = - |FT(p)|^2
I wrote out the formula for the correlation of the two computer outputs, when they are used like I told you (completely random inputs, look at pairs of outputs when pairs of inputs differ by theta).
How those correlations can look like, you can find here
https://arxiv.org/abs/1312.6403The triangle wave versus the cosine: How classical systems can optimally approximate EPR-B correlations
Richard D. Gill
The famous singlet correlations of a composite quantum system consisting of two spatially separated components exhibit notable features of two kinds. The first kind consists of striking certainty relations: perfect correlation and perfect anti-correlation in certain settings. The second kind consists of a number of symmetries, in particular, invariance under rotation, as well as invariance under exchange of components, parity, or chirality. In this note, I investigate the class of correlation functions that can be generated by classical composite physical systems when we restrict attention to systems which reproduce the certainty relations exactly, and for which the rotational invariance of the correlation function is the manifestation of rotational invariance of the underlying classical physics. I call such correlation functions classical EPR-B correlations. It turns out that the other three (binary) symmetries can then be obtained "for free": they are exhibited by the correlation function, and can be imposed on the underlying physics by adding an underlying randomisation level. We end up with a simple probabilistic description of all possible classical EPR-B correlations in terms of a "spinning coloured disk" model, and a research programme: describe these functions in a concise analytic way. We survey open problems, and we show that the widespread idea that "quantum correlations are more extreme than classical physics allows" is at best highly inaccurate, through giving a concrete example of a classical correlation which satisfies all the symmetries and all the certainty relations and which exceeds the quantum correlations over a whole range of settings
Comments: This version, arXiv:1312.6403v.6, as accepted by "Entropy" 27 February 2020
https://www.mdpi.com/1099-4300/22/3/287Nice pictures!

