SciPhysicsForums.com

by **minkwe** » Fri Nov 27, 2020 4:49 pm

What does $(\lambda\sim a^{\pm})$ mean? It appears to be a vector, since you are taking a dot product. But if the result is $\pm 1$ then $(\lambda\sim a^{\pm})$ is just $\pm a$ assuming $a$ is a unit vector. Then it means you are saying $(\lambda\sim a^{\pm})$ is a function $f(\lambda, a) = \pm a$ . But why not just be explicit and show it using the proper notation for a function instead?

Looking at your paper, you do mention in places a polarizer action $\Phi(\lambda, a) = \pm a$ which is exactly the same so why aren't you being consistent?

If you would provide your version of the details of $\Phi(\lambda, a)$ then it would be easier to write down $A(\lambda, a)$ in a way that is actually useful.

One candidate is:

$A(\lambda, a) = \Phi(\lambda, a) \cdot a = ( sign(\lambda \cdot a) a) \cdot a$

which boils down to essentially the same thing as Bell's function.
Thus the real content in your paper appears to be in the details of $\Phi(\lambda, a)$ which you haven't provided.

by **minkwe** » Fri Nov 27, 2020 5:45 pm

One other thing. Is $\Phi(\lambda, a)$ a beam splitter? It looks like it.

See De Raedt's paper https://arxiv.org/pdf/2005.05711.pdf for an example in which they look at event-by-event detailed modeling of beam splitter functions compatible with empirical data and Malus law.

by **Gordon Watson** » Fri Nov 27, 2020 10:42 pm

FrediFizzx wrote:
floccinauci wrote:
floccinauci wrote:What the heck is

$A(a,\lambda)=(\lambda\sim a^{\pm})\!\cdot\!a=\pm1$

With the understanding that a function has three aspects:
- inputs: domain
- transformation
- outputs: range

Please explain using words (no symbols please) in detail for the A(.) case above how the inputs are transformed to produce the outputs. If you could do that, then someone else may be able to help you formulate a better notation for concisely representing it. Your choice of notation is horrendous.

I'm trying to help you but you are not making it easy.

That one is easy. He just means lambda is +/-a. Basically a description of the polarizer action.
.

Thanks Fred. I believe it's all easy. So, with Gill at last proclaiming your genius, let's build on this insight.

1. In my draft, https://vixra.org/abs/2011.0073, for reasons of symmetry: the notation $a^\pm=\pm{a}$ is introduced in §2.2.(ii) in the following context:

1a.

Detector $\delta_{a}^{\pm}(.)$ is a dichotomic (2-channel) polarizer-analyzer with principal-axis $a$ and output channels $a^{\pm}=\pm a$ .

1b. It follows from §2.3.(ii), in the context of a particle $p(.)$ :

$a^\pm$ denotes a particle's post-interaction spin-axis; $p(a^\pm)$ .

2. So my detector-function $\delta_{a}^{\pm}$ anticipates/foreshadows floccinauci's idea

$E_{ab} = \int_{\Lambda} \rho(\lambda) A_a(\lambda)B_b(\lambda)d\lambda$

that, as floccinauci writes,

fixes two notational problems in Bell's original paper: (1) The symbols $a$ and $b$ are labels, not variables since their values do not change during the experiment. (2) I've used $E$ instead of $P$ to denote expectation, which is more standard.

3. For, using Bell's 1964:(14), we can rewrite my (19):

$E(a,b\mid\beta)=-\smallint_{\Lambda} d\lambda\:\rho(\lambda)A(a,\lambda)A(b,\lambda)= -\int_{\Lambda} \rho(\lambda) A_a(\lambda)A_b(\lambda)d\lambda$

$=-\smallint_{\Lambda} d\lambda\:\rho(\lambda)\delta_{a}^{\pm}(\lambda)\delta_{b}^{\pm}(\lambda)$ (19:new).

4. THEN, via a similar denouement to that in my draft:

we arrive at my (26) with Bell's theorem refuted as before.

5. ALL, of course, subject to my detector-functions $\delta_{a}^{\pm}(\lambda)$ and $\delta_{b}^{\pm}(\lambda)$ satisfying the related functions $A(a,\lambda), A(b,\lambda)$ in second term of (19:new) above.

6. Introduced in §3.1.(i): $\overset{\delta_{a}^{\pm}}{\sim}$ is the equivalence relation $\sim$ in the short-form.

$A(a,\lambda)=(\lambda\sim a^{\pm})\!\cdot\!a=\pm1$ , etc.

7. To be continued, and hopefully near-finalised, after I've studied the posts that follow.

Gordon
.

by **gill1109** » Fri Nov 27, 2020 11:03 pm

minkwe wrote:What does $(\lambda\sim a^{\pm})$ mean? It appears to be a vector, since you are taking a dot product. But if the result is $\pm 1$ then $(\lambda\sim a^{\pm})$ is just $\pm a$ assuming $a$ is a unit vector. Then it means you are saying $(\lambda\sim a^{\pm})$ is a function $f(\lambda, a) = \pm a$ . But why not just be explicit and show it using the proper notation for a function instead?

Looking at your paper, you do mention in places a polarizer action $\Phi(\lambda, a) = \pm a$ which is exactly the same so why aren't you being consistent?

If you would provide your version of the details of $\Phi(\lambda, a)$ then it would be easier to write down $A(\lambda, a)$ in a way that is actually useful.

One candidate is:

$A(\lambda, a) = \Phi(\lambda, a) \cdot a = ( sign(\lambda \cdot a) a) \cdot a$

which boils down to essentially the same thing as Bell's function.
Thus the real content in your paper appears to be in the details of $\Phi(\lambda, a)$ which you haven't provided.

“Minkwe”, there is almost no real content in Gordon’s paper. His equation which looks like the definition of a function A actually reduces to the statement “for all a and lambda, A(lambda, a) = A(lambda, a)” once one has deciphered his weird notations. In the paper https://vixra.org/pdf/2011.0073v1.pdf Gordon *never* defines his function A. Instead, he just assumes A, B and rho exist having the usual properties and that they reproduce the singlet correlations in the usual way. He spends several pages on preparatory work not explaining his idiosyncratic notations but mystifying them, while, through abuse of notation, making plenty of room for elementary mistakes in his “elementary probability theory”.

His utterly elementary probability theory goes wrong near the end of the paper, around line (22). This is at the end of the paper where at long last, he gets down to disproving Bell’s three correlation inequality. Well, that inequality was not only proved by Boole in 1853 and Vorobev in 1982, but better still: the set of six one-sided inequalities was shown by those authors to be necessary and sufficient. Fine showed in 1982 that the set of 8 one-sided CHSH inequalities was necessary and sufficient (given the 4 no-signalling equalities).

The discussion on Quora at Gordon’s https://vixra.org/abs/2011.0073 refers to the discussion of Gordon’s previous try https://vixra.org/abs/1812.0437 (and that discussion actually refers to Gordon’s several earlier attempts). A guy called “Mikko” is very patient. Gordon does not understand, he just keeps repeating the same mistake. His mistake is easy to create thanks to his inadequate notation. It is overburdened with superfluous decorations, while at the same time, important parameters are dropped out of the notation. As we have seen, he can’t explain his notation because he does not really know what he is doing, neither in detail nor globally.

As comrade Stalin seems to have written in “Pravda” concerning Shostakovich’s opera “Lady Macbeth of Mtsensk”, “muddle instead of music”.

by **Gordon Watson** » Sat Nov 28, 2020 10:03 pm

floccinauci wrote:
FrediFizzx wrote:That one is easy. He just means lambda is +/-a. Basically a description of the polarizer action.
.

Progress. Then:
$A(a,\lambda) = \Phi(a,\lambda) \cdot a = \pm 1$
where
$\Phi(a,\lambda) = \pm a$

But we need to see the details of the function $\Phi(a,\lambda)$

[Consistent with the above, I'm here not using my preference to distinguish the $\lambda$ going to Alice from that going to Bob.]

Here's what I understood. One of your opening suggestions in this thread was to use $A_a(\lambda)$ for Bell's $A(a,\lambda)$ . I took this to be consistent with my notation: $\delta_a^{\pm}(\lambda)$ .

That is, in searching for the most helpful notation, my motivation was to distinguish the macroscopic detector $\delta_a^{\pm}$ from the microscopic particle $p(\lambda)$ .

Then, within the detector there are 2 functions:

(i). Via the polariser $\Phi_a^{\pm}$ we have $\Phi_a^{\pm}:p(\lambda)\,\rightarrow\,p(a^{\pm})$ ; the output being determined by the equivalence class $[p(a^+)]$ or $[p(a^-)]$ to which $p(\lambda)$ belongs. See §3.1; me now thinking that it might be clearer to replace $\overset{\delta_{a}^{\pm}}{\sim}$ with $\overset{\Phi_{a}^{\pm}}{\sim}$ ??

Note: Bob, via a suitable test in his locale, could tell us (with certainty), which class applied (and thus that class is an element of physical reality). However, absent that knowledge, we must work probabilistically: with each $\lambda$ being a random latent variable from one class or the other.

(ii). Via the analyser, say $\phi_a$ , we have $\phi_a:p(a^{\pm})\,\rightarrow\,{a}\cdot\,a^{\pm}={\pm1}=A^{\pm}$ .

So the detector function $\delta_a^{\pm}(\lambda)$ is the composition of $\phi_a$ and $\Phi_a^{\pm}$ .

And, via short-hand similar to that in (11), I write: $A(a,\lambda)=A_a(\lambda)=\delta_a^{\pm}(\lambda)=A^\pm=\pm\,1$ .

Then, when it seemed some could not complete the related integral, I wrote (for comparison with Bell's use of the sgn function):***

$A(a,\lambda)=A_a(\lambda)=(\lambda\sim a^{\pm})\!\cdot\!a=\pm1$ : using only the variables that contribute to the results.

That is: $(\lambda\sim a^{\pm})$ holds via the equivalence class, $[p(a^+)]$ or $[p(a^-)]$ , to which each $p(\lambda)$ belongs. $a^{\pm}\!\cdot\!a=\pm1$ follows via the analyser function.

*** In my view, the sgn function is too simplistic for the dynamics involved. My function allows for the dynamics associated with spin, torque, precession.

HTH; Gordon
.

by **Gordon Watson** » Sat Nov 28, 2020 10:12 pm

minkwe wrote:What does $(\lambda\sim a^{\pm})$ mean? It appears to be a vector, since you are taking a dot product. But if the result is $\pm 1$ then $(\lambda\sim a^{\pm})$ is just $\pm a$ assuming $a$ is a unit vector. Then it means you are saying $(\lambda\sim a^{\pm})$ is a function $f(\lambda, a) = \pm a$ . But why not just be explicit and show it using the proper notation for a function instead?

Looking at your paper, you do mention in places a polarizer action $\Phi(\lambda, a) = \pm a$ which is exactly the same so why aren't you being consistent?

If you would provide your version of the details of $\Phi(\lambda, a)$ then it would be easier to write down $A(\lambda, a)$ in a way that is actually useful.

One candidate is:

$A(\lambda, a) = \Phi(\lambda, a) \cdot a = ( sign(\lambda \cdot a) a) \cdot a$

which boils down to essentially the same thing as Bell's function.
Thus the real content in your paper appears to be in the details of $\Phi(\lambda, a)$ which you haven't provided.

Thanks for this; I took it too much for granted that the schematics and text relating to a good old polariser were adequate. Please comment critically on my last post.

Thanks again; Gordon
.

by **Gordon Watson** » Sat Nov 28, 2020 10:48 pm

minkwe wrote:One other thing. Is $\Phi(\lambda, a)$ a beam splitter? It looks like it.

See De Raedt's paper https://arxiv.org/pdf/2005.05711.pdf for an example in which they look at event-by-event detailed modeling of beam splitter functions compatible with empirical data and Malus law.

Thanks for the link. Often nervous when time is brought into EPRB, I'm in no position to be too critical.

However, if we insist that Bell's theorem was developed under the EPRB thought-experiment, these [from p.2] surprise me: "While there can be no doubt about the mathematical correctness of Bell’s theorem ...." "Before one can even think about computing correlations of particle properties, it is necessary to first classify a detection event as corresponding to the arrival of a particle or as something else."

So I'm concerned about the functions that they -- consequently -- build into their beam-splitters.

Thus (while believing your view to be OK), I've preferred to stick to old-fashioned terms for old-fashioned devices: for all that I require is that they polarise each input particle and send it to the appropriate output channel.

by **minkwe** » Sun Nov 29, 2020 9:38 pm

Gordon Watson wrote:Consistent with the above, I'm here not using my preference to distinguish the $\lambda$ going to Alice from that going to Bob.]

Here's what I understood. One of your opening suggestions in this thread was to use $A_a(\lambda)$ for Bell's $A(a,\lambda)$ . I took this to be consistent with my notation: $\delta_a^{\pm}(\lambda)$ .

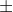
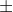
What is the import of $\pm$ for your $\delta^{\pm}$ function. Is it to distinguish Alice and Bob? If so, how would you express the perfect anti-correlation result $A_a(\lambda) = -B_a (\lambda)$ which is appropriate in this case. Using $\pm$ in that way is unnecessary and confusing.

That is, in searching for the most helpful notation, my motivation was to distinguish the macroscopic detector $\delta_a^{\pm}$ from the microscopic particle $p(\lambda)$ .

Please don't use functions to represent particles. There is no reason to introduce notation for particles at all. The only relevant properties of a particle in this context are $\lambda$ and the arm of the experiment in which the particle finds itself, the latter even ignored in some treatments. One other general advice, when ever you introduce notation, it helps to define it. For example, if you must introduce notation for particles you would do something like:

Example wrote:Particles $P_{\lambda}^{\pm}$ are emitted by the source, where $P_{\lambda}^{+}$ heads towards Alice's and $P_{\lambda}^{-}$ towards Bob.

Then, within the detector there are 2 functions:

(i). Via the polariser $\Phi_a^{\pm}$ we have $\Phi_a^{\pm}:p(\lambda)\,\rightarrow\,p(a^{\pm})$ ; the output being determined by the equivalence class $[p(a^+)]$ or $[p(a^-)]$ to which $p(\lambda)$ belongs. See §3.1; me now thinking that it might be clearer to replace $\overset{\delta_{a}^{\pm}}{\sim}$ with $\overset{\Phi_{a}^{\pm}}{\sim}$ ??

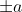
Please no. Polarizers should work the same way irrespective of which arm of the experiment they are located at. A polarizer Transforms a particle so the details should show how the relevant particle properties change. I would change your notation to $\Phi_a(\lambda) = \pm a$ . But you still haven't shown exactly how the transformation happens. Anyway, you write $a^\pm$ instead of $\pm a$ . Please explain why you think the former is more correct, otherwise, the latter is a much better notation. Again, please stay clear of using functions to denote particles.

Note: Bob, via a suitable test in his locale, could tell us (with certainty), which class applied (and thus that class is an element of physical reality). However, absent that knowledge, we must work probabilistically: with each $\lambda$ being a random latent variable from one class or the other.

(ii). Via the analyser, say $\phi_a$ , we have $\phi_a:p(a^{\pm})\,\rightarrow\,{a}\cdot\,a^{\pm}={\pm1}=A^{\pm}$ .

In other words, you are saying you don't know how the transformation happens. Does the polarizer analyzer combination need any additional information except the setting $a$ and particle property $\lambda$ to produce an outcome $\pm 1$ ? If not you need to explain why the result is probabilistic and not deterministic.

So the detector function $\delta_a^{\pm}(\lambda)$ is the composition of $\phi_a$ and $\Phi_a^{\pm}$ .

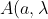Yes, I figured. This is a longwinded way of going about it. Traditionally, Bell's function $A(a, \lambda)$ is understood to include everything required to generate an outcome $\pm 1$ . Thus, while everything you have described polarizers and analyzers and detectors may be interesting to you, they are superfluous to anyone else familiar with these types of analyses. You will do your audience a lot of good by going straight to $A(a,\lambda)=A_a(\lambda)=\pm\,1$ . I've deliberately omitted $\delta_a^{\pm}(\lambda)=A^\pm$ because it is problematic. I think you are focusing too much on equivalence classes because it allows you to segway to the probability analysis. However, combining it together with $\lambda$ in that way is not proper. At best it is an abuse of notation because the common understanding of the meaning of $\lambda$ in Bell literature is not restricted to equivalence classes of lambda that produce specific outcomes. If you must do that, then you must introduce the concept and new notation to boot. 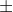I think I see now clearly why you are struggling with $\pm$ superscripts. But there is an easier way. You don't have to do that at all.

See this post from "floccinauci" viewtopic.php?f=6&t=451&start=120#p12137.

Especially since all the polarizer/analyzer/detector stuff is superfluous anyway, you can go directly to the probability treatment. No need to mention anything about the details of the functions if you don't know them.

However, if you are going to demonstrate that a function is able to generate the probability result, which is an interesting exercise in its own right (probably more so), then if and when you provide the functions, they better contain details and not rely on the same probabilities to generate outcomes. You need to show the mechanics.

Then, when it seemed some could not complete the related integral, I wrote (for comparison with Bell's use of the sgn function):***

Please no. If I give you a specifc vector $\lambda_k = [0.1249, 0.7497, -0.6597]$ at Alice's station, and a specific setting vector $a = [0.5, 0.866, 0]$ . Please can you calculate the outcome for that specific particle, step by step using $(\lambda\sim a^{\pm})\cdot a$ . If you can't, please explain why you can't.

*** In my view, the sgn function is too simplistic for the dynamics involved. My function allows for the dynamics associated with spin, torque, precession.

You haven't shown us anything about this "dynamics". This is what I've been asking for.

Anyone can say "the sign function is too simplistic, the function 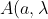$A(a, \lambda) = \pm 1$ allows for the dynamics associated with spin, torque, precession". How is this different from what you are saying above, until you provide such a function? It is not sufficient to just replace Bell's notation with yours and claim dynamics. The sign function so far has the advantage that it is transparent about what it thinks is going on, even if it is wrong.

by **Gordon Watson** » Sun Nov 29, 2020 11:37 pm

Dear minkwe,

Many thanks for your good comments, suggestions, questions, misunderstandings, attitude, etc. Learning much from such, I expect us to reach 100% agreement.

To that end, I will be cutting your post into smaller pieces. That way it should be easier for me to keep pace with ongoing Q&As.

Thanks again; Gordon
.

by **Gordon Watson** » Mon Nov 30, 2020 12:20 am

minkwe wrote:
Gordon Watson wrote:[Consistent with the above, I'm here not using my preference to distinguish the $\lambda$ going to Alice from that going to Bob.]

Here's what I understood. One of your opening suggestions in this thread was to use $A_a(\lambda)$ for Bell's $A(a,\lambda)$ . I took this to be consistent with my notation: $\delta_a^{\pm}(\lambda)$ .

(1) What is the import of $\pm$ for your $\delta^{\pm}$ function. (2) Is it to distinguish Alice and Bob? (3) If so, how would you express the perfect anti-correlation result $A_a(\lambda) = -B_a (\lambda)$ which is appropriate in this case. (4) Using $\pm$ in that way is unnecessary and confusing.

It seems that we begin here with major misunderstandings.

1. In $\delta_a^{\pm}$ , $\delta$ denotes a detector: all detectors here being the same,** except for the orientation (here $a$ ) of their principal axis.

The superscript $\pm$ denotes (in EPRB) the two output channels in relation to the principal axis: $a^{\pm}$ ; ie UP or DOWN.

Thus, in experiments where (say, in early lectures) we wanted only the UP outputs, a detector would be denoted $\delta_a^{+}$ .

Q: I have used $\Delta_a^{\pm}$ , and am thinking it preferable? Comment welcome.

2. Here, the subscript $a$ in $\delta_a^{\pm}$ tells you that it is in Alice's locale.

3. The perfect anti-correlation can be seen at the end of §2.2. And in this case you know that the second subscript $a$ refers to Bob's detector since its argument is $\lambda^-$ .

4. It seems to me that I do not use them as you suppose.

** A point you make elsewhere, and we agree.

HTH, Gordon
.

by **minkwe** » Mon Nov 30, 2020 5:56 am

Gordon Watson wrote:It seems that we begin here with major misunderstandings.

1. In $\delta_a^{\pm}$ , $\delta$ denotes a detector: all detectors here being the same,** except for the orientation (here $a$ ) of their principal axis.

The superscript $\pm$ denotes (in EPRB) the two output channels in relation to the principal axis: $a^{\pm}$ ; ie UP or DOWN.

The misunderstandings are caused by your choice of notation. You are mixing up symbols used to label detectors with functions on how those detectors work. There is absolutely no reason for the $\delta_a^{+}$ to be different in its detailed functioning mechanism from the $\delta_a^{-}$ detector. Since all your detectors work exactly the same way, when you write the function $\delta_a^{\pm}(\lambda)$ it serves no purpose than to cause confusion.

Thus, in experiments where (say, in early lectures) we wanted only the UP outputs, a detector would be denoted $\delta_a^{+}$ .

That's fine as a detector label.

Q: I have used $\Delta_a^{\pm}$ , and am thinking it preferable? Comment welcome.

It is better to label the detectors $\Delta_a^{\pm}$ and to use $\delta_a(\lambda)$ for the function or even better $A_a(\lambda)$ and $B_b(\lambda)$ .

2. Here, the subscript $a$ in $\delta_a^{\pm}$ tells you that it is in Alice's locale.

That's fine as a label but not as a function.

by **minkwe** » Mon Nov 30, 2020 7:01 am

Gordon Watson wrote:3. The perfect anti-correlation can be seen at the end of §2.2. And in this case you know that the second subscript $a$ refers to Bob's detector since its argument is $\lambda^-$

You have $\delta_{a}^{\pm}(\lambda^+) = -\delta_{a}^{\pm}(\lambda^-)$ with emphasis on the fact that the particle going to Alice has different but complementary properties to those going to Bob which seems fine but unnecessarily complex. Bell subsumes the differences between the particles into different functions $A(\cdot)$ and $B(\cdot)$ .

In anycase, don't you see that your $\pm$ superscripts for $\delta$ are superfluous and confusing?? Otherwise please explain what the following means:

$\delta_{a}^{+}(\lambda^+) = -\delta_{a}^{+}(\lambda^-)$

by **minkwe** » Mon Nov 30, 2020 3:18 pm

gill1109 wrote:“Minkwe”, there is almost no real content in Gordon’s paper. His equation which looks like the definition of a function A actually reduces to the statement “for all a and lambda, A(lambda, a) = A(lambda, a)” once one has deciphered his weird notations.

That's not a fair characterization.

His utterly elementary probability theory goes wrong near the end of the paper, around line (22). This is at the end of the paper where at long last, he gets down to disproving Bell’s three correlation inequality.

I think you've misunderstood equation 22 which is representing a single Expectation value (correlation) not the 3-correlation version as you say. What Gordon is doing is just calculating a single expectation $E(a,b)$ using probability theory and showing that he can easily reproduce the quantum result using simple probability theory.

The discussion on Quora at Gordon’s https://vixra.org/abs/2011.0073 refers to the discussion of Gordon’s previous try https://vixra.org/abs/1812.0437 (and that discussion actually refers to Gordon’s several earlier attempts). A guy called “Mikko” is very patient. Gordon does not understand, he just keeps repeating the same mistake. His mistake is easy to create thanks to his inadequate notation. It is overburdened with superfluous decorations, while at the same time, important parameters are dropped out of the notation. As we have seen, he can’t explain his notation because he does not really know what he is doing, neither in detail nor globally.

Gordon may be stubborn but he is not stupid. He is doing something very smart. If only he would get out of his own way

, it would become more apparent.

by **Gordon Watson** » Mon Nov 30, 2020 4:40 pm

minkwe wrote:
Gordon Watson wrote:It seems that we begin here with major misunderstandings.

1. In $\delta_a^{\pm}$ , $\delta$ denotes a detector: all detectors here being the same,** except for the orientation (here $a$ ) of their principal axis.

The superscript $\pm$ denotes (in EPRB) the two output channels in relation to the principal axis: $a^{\pm}$ ; ie UP or DOWN.

The misunderstandings are caused by your choice of notation. You are mixing up symbols used to label detectors with functions on how those detectors work. There is absolutely no reason for the $\delta_a^{+}$ to be different in its detailed functioning mechanism from the $\delta_a^{-}$ detector. Since all your detectors work exactly the same way, when you write the function $\delta_a^{\pm}(\lambda)$ it serves no purpose than to cause confusion.

Thus, in experiments where (say, in early lectures) we wanted only the UP outputs, a detector would be denoted $\delta_a^{+}$ .

That's fine as a detector label.

Q: I have used $\Delta_a^{\pm}$ , and am thinking it preferable? Comment welcome.

It is better to label the detectors $\Delta_a^{\pm}$ and to use $\delta_a(\lambda)$ for the function or even better $A_a(\lambda)$ and $B_b(\lambda)$ .

2. Here, the subscript $a$ in $\delta_a^{\pm}$ tells you that it is in Alice's locale.

That's fine as a label but not as a function.

Maybe I'm being too idealistic? And maybe I need to be less so: so that we can move ahead?

For I have no wish, as I hope you'll come to see, to reject an adequate notation.

-----------------------------------------

SO, E&OE: Do we agree to proceed with:

Bell's $A(a,\lambda)=A_a(\lambda^+)=A_a(\lambda)=\pm1$ ?

Bell's $B(b,\lambda)=A_b(\lambda^-)=-A_b(\lambda)=\pm1$ ?

Bell's $A(a,\lambda)B(a,\lambda)=-A_a(\lambda)A_a(\lambda)=-1$ ?

-----------------------------------------

Then, for the record, and hopefully making some of my past drafts clearer:

I seek to identify an existent via the same symbol in the schematics, text, and mathematics.

So, I ask myself: for $A_a(\lambda^+)$ , why not use $\Delta_a^{\pm}(\lambda^+)$ ; etc?

So the reader understands -- in the mathematics, text, schematics -- that we are dealing with a two-channel detector, its principal axis set to $a$ .

Then, re this from you:

There is absolutely no reason for the $\delta_a^{+}$ to be different in its detailed functioning mechanism from the $\delta_a^{-}$ detector. Since all your detectors work exactly the same way, when you write the function $\delta_a^{\pm}(\lambda)$ it serves no purpose than to cause confusion.

$\delta_a^{+}$ would pass the post-interaction spin-up particles and absorb the post-interaction spin-down particles. $\delta_a^{-}$ would pass the post-interaction spin-down particles and absorb the post-interaction spin-up particles.

Feynman might have liked them, for his lectures on Stern-Gerlach?

by **Gordon Watson** » Mon Nov 30, 2020 5:02 pm

minkwe wrote:
Gordon Watson wrote:3. The perfect anti-correlation can be seen at the end of §2.2. And in this case you know that the second subscript $a$ refers to Bob's detector since its argument is $\lambda^-$

You have $\delta_{a}^{\pm}(\lambda^+) = -\delta_{a}^{\pm}(\lambda^-)$ with emphasis on the fact that the particle going to Alice has different but complementary properties to those going to Bob which seems fine but unnecessarily complex. Bell subsumes the differences between the particles into different functions $A(\cdot)$ and $B(\cdot)$ .

In anycase, don't you see that your $\pm$ superscripts for $\delta$ are superfluous and confusing?? Otherwise please explain what the following means:

$\delta_{a}^{+}(\lambda^+) = -\delta_{a}^{+}(\lambda^-)$

1. That "complexity" -- favoured by me and allowed by Bell (1964), last paragraph in II: Formulation -- is designed to stymie those who say that "Bell's $\lambda$ is a valid non-local beable." (The source currently escapes me.)

2. Your example has no rational meaning for me: except that it must be false. For, with your single-channel detectors passing only post-interaction spin-up particles, that first minus-sign is problematic.

by **minkwe** » Mon Nov 30, 2020 5:27 pm

Gordon Watson wrote:SO, E&OE: Do we agree to proceed with:

Bell's $A(a,\lambda)=A_a(\lambda^+)=A_a(\lambda)=\pm1$ ?

Bell's $B(b,\lambda)=A_b(\lambda^-)=-A_b(\lambda)=\pm1$ ?

Bell's $A(a,\lambda)B(a,\lambda)=-A_a(\lambda)A_a(\lambda)=-1$ ?

Much better.

So, I ask myself: for $A_a(\lambda^+)$ , why not use $\Delta_a^{\pm}(\lambda^+)$ ; etc?

So the reader understands -- in the mathematics, text, schematics -- that we are dealing with a two-channel detector, its principal axis set to $a$ .

No because $\Delta_{a}^{\pm}$ is a label of a detector where a particle may end up. Not unlike a schematic drawing of the experimental setup. It is not a function or an outcome. So doing this is going back to the earlier confusion. If you want the reader to understand that you are dealing with a two channel-detector, draw a schematic diagram and label it. Not this. Or just use text to describe it. Don't mix it into the functions. A particle that ends up at $\Delta_a^+$ is recorded in Alice's logbook as an outcome of $+1$ . The fact that the outcomes at each station can have values $\pm 1$ already implies that each station has a two-channel detector. You won't be adding any information by doing this, just more confusion.

$\delta_a^{+}$ would pass the post-interaction spin-up particles and absorb the post-interaction spin-down particles. $\delta_a^{-}$ would pass the post-interaction spin-down particles and absorb the post-interaction spin-up particles.

Ahhh! So your detector is not 100% efficient?! Since $\delta^+$ only detects spin-up and $\delta^-$ . Spin down? This is actually bad because it pushes your train off the rails unnecessarily. Follow along for a moment.

What if you reject the idea of detecting spin-up and absorbing spin-down. Instead, consider that you have a beam-splitter $\Phi_a$ and a two-channel detector assembly. Your beam splitter splits the incoming particle by projecting it to either the $\Delta_a^+$ detector channel of the station or the $\Delta_a^-$ detector channel. In this case, your detectors don't need to be different, or inefficient. They simply detect everything that impinges on them to generate a signal. if $\Delta^+$ lights-up, Alice records +1 and if $\Delta^-$ lights-up, she records -1. No need to reject any spin-up or spin-down particles anywhere. And no need for non-detection events. Won't this be better?

Alternatively, imagine the whole thing at Alice is just a black box with a screen that displays either -1 or +1 based on what happened. No need for polarizer or detector. The analysis should not be different. In both cases it is interesting to provide a mechanism used to covert $\lambda$ to the outcomes. Whether you use a single function or break it down into one function for a polarizer, another for the fibre-optic cable, another for the detector, etc, etc is just irrelevant fluff. That is why a fully detailed out $A(\cdot)$ function is important. Leave the experiment to those doing experiments and focus on the analysis.

by **minkwe** » Mon Nov 30, 2020 5:38 pm

Gordon Watson wrote:
minkwe wrote:In anycase, don't you see that your $\pm$ superscripts for $\delta$ are superfluous and confusing?? Otherwise please explain what the following means:

$\delta_{a}^{+}(\lambda^+) = -\delta_{a}^{+}(\lambda^-)$

2. Your example has no rational meaning for me: except that it must be false. For, with your single-channel detectors passing only post-interaction spin-up particles, that first minus-sign is problematic.

Exactly! That equation is implied by your notation which you used to express perfect anti-correlation in section 2.2 of your paper. If it doesn't make sense even to your then you shouldn't be using that notation.

by **Gordon Watson** » Mon Nov 30, 2020 5:53 pm

Continuing:

minkwe wrote:
Gordon Watson wrote:
That is, in searching for the most helpful notation, my motivation was to distinguish the macroscopic detector $\delta_a^{\pm}$ from the microscopic particle $p(\lambda)$ .

minkwe wrote:(1). Please don't use functions to represent particles. (2). There is no reason to introduce notation for particles at all. (3). The only relevant properties of a particle in this context are $\lambda$ and the arm of the experiment in which the particle finds itself: (4). the latter even ignored in some treatments. (5). One other general advice, when ever you introduce notation, it helps to define it. (6). For example, if you must introduce notation for particles you would do something like:

minkwe wrote:Particles $P_{\lambda}^{\pm}$ are emitted by the source, where $P_{\lambda}^{+}$ heads towards Alice's and $P_{\lambda}^{-}$ towards Bob.

(1). I do not use functions to represent particles. See §2.2.(i). For me, the convenience of this notation is that I can extract and discuss extensive particle-properties; see next.

(2). I introduce particles in the schematics of eqns (7)-(10). There, for example, I want to show the transformation of pristine $p(\lambda^+)$ to post-interaction $p(a^\pm)$ ; etc. More importantly: I can include many properties in my $(.)$ . See (15)-(17). Which is handy when I want to show that Alice's results and Bob's results are determined -- in full accord with relativistic-causality -- by local properties alone.

(3). Re relevance, I like to show that a locally-polarised particle [not spooky action] triggers the result; eg, $A^+=1$ .

(4). Yes. However, I believe it is clearer if we recognise the following EPRB fact explicitly: the pristine particle properties are pair-wise anti-correlated. So, pair-wise, I allow that $p(\lambda^+)$ flies to Alice, and $p(\lambda^-)$ to Bob. [Under TLR, no possibility of non-local beables for me.]

(5). Reinforcing what I already work hard to do: advice/reminder gratefully accepted, with thanks. See #1 above.

(6). Having rebutted the idea that I'm using functions here -- see #1 above -- I'm hoping you can agree to proceed via that handy notation: $p(.......)$ ?

Unless I've missed something?

Thanks; Gordon
.

by **minkwe** » Mon Nov 30, 2020 6:23 pm

Gordon Watson wrote:(1). I do not use functions to represent particles. See §2.2.(i). For me, the convenience of this notation is that I can extract and discuss extensive particle-properties; see next.

You are re-using function notation for representing particles then which is even worse. Bad idea, don't do it.

(2). I introduce particles in the schematics of eqns (7)-(10). There, for example, I want to show the transformation of pristine $p(\lambda^+)$ to post-interaction $p(a^\pm)$ ; etc. More importantly: I can include many properties in my $(.)$ . See (15)-(17). Which is handy when I want to show that Alice's results and Bob's results are determined -- in full accord with relativistic-causality -- by local properties alone.

You can show that more clearly with my suggested notation than yours without the confusion of what appears to be a function but is not:

$P_{\lambda}^{+} \rightarrow P_{a}^{\pm}$ is better.

I'm not questioning your rationale for wanting to show the transformation of pristine particles to post-interaction particles. I'm questioning your choice of notation for doing so.

(3). Re relevance, I like to show that a locally-polarised particle [not spooky action] triggers the result; eg, $A^+=1$ .
(4). Yes. However, I believe it is clearer if we recognize the following EPRB fact explicitly: the pristine particle properties are pair-wise anti-correlated. So, pair-wise, I allow that $p(\lambda^+)$ flies to Alice, and $p(\lambda^-)$ to Bob. [Under TLR, no possibility of non-local beables for me.]

You can also describe it using words without cramming everything into equations.

(6). Having rebutted the idea that I'm using functions here -- see #1 above -- I'm hoping you can agree to proceed via that handy notation: $p(.......)$ ?
.

Please no. The notation is not handy, it is counter-productive and doesn't help your cause. I hope you would see that. If you want a particle to be represented by a set of properties, then use the proper notation for that like $\{ \lambda, ... \}$

by **Gordon Watson** » Mon Nov 30, 2020 6:39 pm

So how about going with $p\{ \lambda, ... \}$ ; etc?

Your $P$ notation looks too much like a probability for me.

SciPhysicsForums.com

Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Re: Bell's theorem refuted via elementary probability theory

Who is online