AnotherGuest wrote:Very good question, Minkwe.
We can speak meaningfully about what would happen if ... . All physics is about saying what would happen if ....
But we are examining the definition of "counterfactual definiteness" used in the literature, and are finding that either they come up short or they also apply to QM. I didn't come up with the definition.
Counterfactual definiteness goes, I think, beyond that. It is about the question whether all those other things which could have happened if .. are to be considered just as real as the one thing that does actually happen in the circumstances which will actually hold.
But according to QM, if Alice obtains +1 along "a", Bob must also definitely obtain -1 if he measures along "a". It does not matter whether Bob actually measured along a different axis "b". QM says if Bob had measured along "a", he would definitely have obtained -1. This is counterfactual definiteness according to the definition being used in the literature. If you disagree could you please show a source where counterfactual definiteness is defined differently such that it does not apply to this situation. We are not just playing with words, we are decifering exactly what people talk about when they use those terms. First we found that when people say "locality" they don't actually mean "locality", they mean "setting and outcome independence", which applies equally to local or non-local situations. Now we are finding that when people say "counterfactual definiteness", they either mean something else than their own definitions claim it means, or if their definitions are to be followed, it should apply to QM just the same.
Word games for philosophers. But as soon as we start talking about mathematical models, then we do get onto something interesting, I think.
There is a reason why when you get a terminal degree it is called a PhD -- Doctor of philosophy. Philosophy is an integral part of any scientific endeavor. It is very unfortunate that "philosophy" is nowadays considered a derogatory term in some mathematics/physics circles.
We can ask the question: is there a mathematical model which reproduces the predictions of quantum mechanics,
Indeed that is an interesting question. But our focus at the moment is on a specific but different question: What are the physical assumptions required to obtain Bell's inequalities. We've seen that despite popular belief, "locality" is not one of those assumptions. Now we are seeing that the "popular" definition of "counterfactual definiteness" actually applies to Bell's description of the QM prediction too. The concept of couterfactual definiteness is completely irrelevant if our goal is to develop a model for
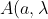)
.
but which also goes beyond those predictions and allows, within the mathematics, "existence" of counterfactual outcomes of not performed measurements, alongside of actual outcomes of actually performed measurements
...
I think that the whole discussion is not actually about "reality" (whatever that is!) but about mathematical models of reality. And about whether those mathematical models can be extended so as to include also "what would have happened if ...". And about whether that extended model still satisfies natural locality properties.
So you believe the statement

Does not apply to QM? Is that a mathematical model?
Note that in Bell's derivation of the inequalities, the actual details of the functions
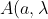)
are irrelevant. The derivations rely entirely on the symbols and the outcomes of the functions, not the models. In fact, I presented a derivation above which used just the three outcomes

, no functions. Therefore it is a grave mistake to think that Bell's derivation is about any mathematical models. It is about series of triplets of bivalued numbers

. Besides, if a model were to provide a definition for the function
)
, there would be no reason whatsoever for that model to include any concept of counterfactual definiteness in the function. What use would that be?
In other words, local-ness or not local-ness is a property of a model
I agree, locality or non-locality can be a property of a model. But I claim that counterfactual definiteness is not a property of a model. A model is local if its definition of the function A_a(...) uses only information within the light-cone. It is non-local if its definition of the function uses information from outside the light-cone. But what does it mean for a model to be counterfactually definite? It is a completely irrelevant concept as far as models of the outcomes in the EPRB experiment are concerned. In other words, counterfactual definiteness is completely irrelevant to the question of whether or not a model reproduces the QM predictions. The only reason we are discussing it is because it was invoked by Bell in deriving his inequalities.
I do not contest the fact that Bell's inequality as far as it applies to experimental tests, includes a mixture of actual and counterfactual outcomes. It is not the theory that forces Bell to do that, it is Bell himself who simply introduced that into his inequality.

