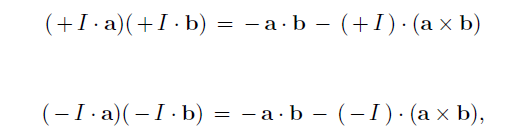Lockyer's math error

[Joy Christian]

***

So we have two equations in classical mechanics:



and



where are the generators of angular momenta.

Are these two equations correct? Are both of them correct? Are both of them wrong? Is only one of them correct? If that is the case, then which one?

***

Perhaps this paper is relevant? See equation (5.18)

http://campus.mst.edu/physics/courses/4 ... apter7.pdf

Indeed it is relevant.

I was hoping that our detractors would come out and claim that the first equation above, with the + sign, is wrong -- i.e., it has a "sign error" -- but no one apart from Mikko took my bait. And even he did not object to the + sign. Rightly so, because it is the standard equation of classical mechanics, with the + sign stemming from Hamilton's quaternions. But now look back to what Lockyer has been claiming above. What he is claiming is that the + sign in the first equation is wrong, thus he is contradicting many standard textbook treatments of angular momenta in both classical and quantum mechanics. In fact, the above two equations immediately imply



and



respectively, thus leading us back to Lockyer's multiplication tables above. In short, this little demonstration once again shows how clueless Lockyer and company have been, both about physics as well as about mathematics. And it is I who has been paying a heavy price for their stupidity.

By the way, in the language of geometric algebra the above two equations are nothing but the left and right handed bivector subalgebras that are found in my papers.

[FrediFizzx]

I was hoping that our detractors would come out and claim that the first equation above, with the + sign, is wrong -- i.e., it has a "sign error" -- but no one apart from Mikko took my bait. And even he did not object to the + sign. Rightly so, because it is the standard equation of classical mechanics, with the + sign stemming from Hamilton's quaternions. But now look back to what Lockyer has been claiming above. What he is claiming is that the + sign in the first equation is wrong, thus he is contradicting many standard textbook treatments of angular momenta in both classical and quantum mechanics. In fact, the above two equations immediately imply



and



respectively, thus leading us back to Lockyer's multiplication tables above. In short, this little demonstration once again shows how clueless Lockyer and company have been, both about physics as well as about mathematics. And it is I who has been paying a heavy price for their stupidity.

By the way, in the language of geometric algebra the above two equations are nothing but the left and right handed bivector subalgebras that are found in my papers.

That is probably too advanced for Lockyer and the others to understand. After all, they don't even seem to understand the simple left and right handed vector cross product difference. Somehow we have got to get people to better understand exactly what is going on. It is actually quite a thing of beauty.

[Rick Lockyer]

The second equation on the left is equal to the first equation on the left, because the two minus signs on the I terms cancel each other out. The sign error is clearly presented by Christian by the fact the two right handed sides are not equal.

I am thinking everybody can see this is so. But what do we get from Joy and his supporters? Repeated nonsense, obfuscation, bluffing and true straw-man arguments like Lockyer thinks this, Lockyer thinks that, Lockyer does not understand physics.

The oddest of all is Diether's claim I do not think there are left and right handed screws. What is next? Is he going to claim if he drops a right handed screw into an empty sack, then drops in a left handed screw, the sack will then be empty??

It is truly sad that the cover up of an initial published error grew orders of magnitude worse than the original mistake. Christian, nobody is doing anything to you, you have done it all to yourself. Too bad.

[Joy Christian]

The second equation on the left is equal to the first equation on the left, because the two minus signs on the I terms cancel each other out. The sign error is clearly presented by Christian by the fact the two right handed sides are not equal.

Lockyer's ignorance and incompetence in basic physics and elementary mathematics are absolutely breathtaking. They are in full display in his comments above. It is beyond belief that he continues to spew his sophomoric nonsense, which is now repeatedly exposed and debunked, especially by Fred in his initial post in this thread.

But let us look at his misconceptions once again. The two equations he has posted above represent two "hidden variable" possibilities. Lockyer has absolutely no clue what that means, for he has zero understanding of what actually happens in the EPR-Bohm type experiments. In any case, the above two equations are equivalent to the following two standard equations of classical mechanics, which --- once again --- are taken as two "hidden variable" possibilities within my local-realistic model:



and



where are the generators of angular momenta. Let me stress that these are standard equations and can be found in many textbooks on classical mechanics.

They immediately imply



and



respectively, demonstrating that the first of my two equations above describes right-handed bivectors and the second one describes left-handed bivectors.

As I noted above, this shows once again how clueless Lockyer and company have been, both about physics as well as about mathematics. One has to be either extraordinarily thick or shockingly disingenuous to not understand such a simple explanation, despite its presentation 8 years ago in my very first paper on Bell.

There is no sign error. If you do not see what has been explained to you yet then it is you who is incompetent. If you do see it but can't admit your error, then you are being disingenuous. Your arguments on this thread are not about Joy's model, but rather a figment of your imagination.

Although he is banned from this forum (just as he is banned from Paul Snively's blog), Richard Gill has "kindly" sent me the following admission in a private email:

I am delighted to admit that I had overlooked the intended interpretation of your two equations: the interpretation which makes them entirely consistent with one another. In retrospect, very obvious ...

This was sent to me in a private email after he saw my following earlier post in this thread:

* * *


Well, Lockyer seems to have finally recognized his error. I hope he has the courage to admit his error in public (I expect no such decency from Gill and Moldoveanu).

Let me spell out the key point explicitly here so there remains no doubt in anyone's mind. The mathematical demonstration is exceedingly simple and easy to follow.

What we want to show is that the first equation above (as written by me in these two papers) forms a right-handed system; and the second equation (again, as written by me in these two papers) forms a left-handed system. Gill, Moldoveanu, and Lockyer falsely claim that I have made a sign error on the RHS of the second equation.

To check the handedness of these equations, let us set the angle between and to be 90 degrees and define for this case. Now multiply (using the geometric product) the first equation, on both sides, by , from the left. Since we have set and to be orthogonal to each other, and since all bivectors such as square to , the first equation (in this special case of orthogonal and ) reduces to



Now if we follow the same procedure for the second equation -- this time using the bivector , it also reduces to



So far so good. Both equations, as long as they remain "unaware" of each other, can be taken to represent a right-handed system, because their RHS equals to .

But now suppose we wish to compare the two systems, as done in the successive trials of EPR-B type experiments ( is the spin "up", or "down" in a given trial? ). Then we must find a functional mapping between the two equations. But that is a trivial task in the present set up, since we see that the respective bivectors are related as



for any directional vector . If we now substitute the above mapping in the second of the two equations we have derived, we obtain at once, for this second system,



Thus we see at once that the second equation represents a left-handed system with respect to the first system, because now the RHS of this equation equals to .

In conclusion, a sign mistake has indeed been made for the past several years, but it is made by Gill, Moldoveanu, and Lockyer. They should go back to their schools.

[FrediFizzx]

Yeah, and I already told Lockyer to forget about (-I.a)(-I.b) a bunch of times since he can't figure it out and it bothers him so much. It is not really needed anyways but the poor guy is in so much denial from his math error being exposed, he has nothing left to harp about. And he can't even see that his math error is the equivalent of saying that a left handed screw is the same as a right handed screw. Completely absurd.

[Joy Christian]

Yeah, and I already told Lockyer to forget about (-I.a)(-I.b) a bunch of times since he can't figure it out and it bothers him so much. It is not really needed anyways but the poor guy is in so much denial from his math error being exposed, he has nothing left to harp about. And he can't even see that his math error is the equivalent of saying that a left handed screw is the same as a right handed screw. Completely absurd.

I am still shaking my head thinking about the colossal stupidity of Lockyer's "argument" above:

The second equation on the left is equal to the first equation on the left, because the two minus signs on the I terms cancel each other out. The sign error is clearly presented by Christian by the fact the two right handed sides are not equal.

He is claiming that since LHS's of the following two equations are the same but RHS's are not, all the standard textbooks on classical mechanics have a "sign error."



or



where are the generators of angular momenta.

[FrediFizzx]

"Ignorance is curable;
Stupid is forever"

Looks like Lockyer is going to cling to stupid and never admit to his math error.

[Joy Christian]

"Ignorance is curable;
Stupid is forever"

Looks like Lockyer is going to cling to stupid and never admit to his math error.

Just to reassure our readers that I am not making the above point up impromptu, let me stress that it has been explained to Lockyer and company literally thousands of times, in many blog posts and published papers, for many years. See, for one example, the following clear-cut paragraph, reproduced from one of my 2010 papers:

[Rick Lockyer]

The right hand sides of the two equations here

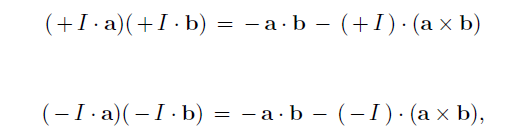
are Christian's "fair coin choices of orientation", one for lambda = +1 and the other for lambda = -1. So please no more BS about this not being essential to Christian's program as in

Yeah, and I already told Lockyer to forget about (-I.a)(-I.b) a bunch of times since he can't figure it out and it bothers him so much. It is not really needed anyways but the poor guy is in so much denial from his math error being exposed, he has nothing left to harp about. And he can't even see that his math error is the equivalent of saying that a left handed screw is the same as a right handed screw. Completely absurd.

I have it figured out Diether. Summing these on an equal chance basis is exactly how Christian tried to demonstrate the -cos() function. Your tying the algebra to physical screws brought me to the one right handed screw plus one left handed screw is the same as no screws. It follows directly from your confusion.

I am still shaking my head thinking about the colossal stupidity of Lockyer's "argument" above:

The second equation on the left is equal to the first equation on the left, because the two minus signs on the I terms cancel each other out. The sign error is clearly presented by Christian by the fact the two right handed sides are not equal.

He is claiming that since LHS's of the following two equations are the same but RHS's are not, all the standard textbooks on classical mechanics have a "sign error."



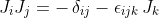
or



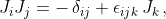
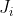
where are the generators of angular momenta. [snipped childish emoticons]

Call the first J set f_ and the second e_ and I will have no issue with these, clearly since they demonstrate portions of the f (left handed) and e (right handed) isomorphic representations of the bivector basis subalgebra of geometric algebra you chose.

You make them both J to provide the illusion they can be added, as you do in adding fair coin choices between left and right handed orientations. So why not, lets add both just for s*** and giggles, and put a happy face on it after dividing by 2. What have we proved? Simply that the product of ANY two unit bivectors is either 0 or -1, since the non-scalar portion drops out due to the opposite signs within the two added equations. Not sure about you two, but the rest of us are going to have issues with this conclusion.

I call one basis e and the other f, and ALWAYS include the basis elements in the math for good reason. It clearly indicates which coefficients can be directly added and which can't. The coefficients on like enumerated basis elements for the two orientations are of opposite sign, the problem is the attached basis element is not the same, and when made the same an additional negation is required. This negation is precisely the minus sign in (-I.a) as compared to (I.a), which Christian correctly assigns as his left and right orientations respectively. Only an idiot would conclude it is an extra negation.

As for Christian's "the colossal stupidity of Lockyer's "argument" above:", just what is it you do not understand about the two minus signs on the left hand side of the second equation cancel, making it the same as the left hand side of the first equation in this:

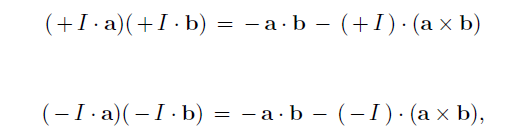
No obfuscation, BS, just YOUR math equations. The rule of multiplication by a real number (-1 here) is going to prevent you from doing this. Your sign error is quite real, the proof is quite trivial, making your insistence there is none quite amazing.

Michel Fodje, Christian keeps putting you in his club of stupid people by repeating your slight towards me. Now I can give you the benefit of the doubt that you did not look closely enough at things, and accept your apology. But if you still think I am the one that made the math error, you got some 'splaining to do Lucy. Man up, something Christian and Diether et al don't seem able to do. Please do tell us how (-1)(-1) does not equal +1.

[FrediFizzx]

Yep, totally stuck on stupid. Lockyer will just keep making a fool of himself no matter what. Just can't ever admit to a math error. It is so clear from my OP that he double translated his f_ elements. A left handed screw is the same as a right handed screw by Lockyer's math. It is absurd.

[Joy Christian]

Yep, totally stuck on stupid.

Indeed. Let him be. We are done. If he wishes to keep flaunting his incompetence and disingenuousness, then that is his choice. Michel had him figured out right:

There is no sign error. If you do not see what has been explained to you yet then it is you who is incompetent. If you do see it but can't admit your error, then you are being disingenuous. Your arguments on this thread are not about Joy's model, but rather a figment of your imagination.

Just to reassure our readers that I am not making the above point up impromptu, let me stress that it has been explained to Lockyer and company literally thousands of times, in many blog posts and published papers, for many years. See, for one example, the following clear-cut paragraph, reproduced from one of my 2010 papers:



PS: I should point out here for those unfamiliar with my work that the above sign ambiguity is taken as two "hidden variable" possibilities in my local-realistic model.

[FrediFizzx]

PS: I should point out here for those unfamiliar with my work that the above sign ambiguity is taken as two "hidden variable" possibilities in my local-realistic model.

And to further point out that it takes at least a particle pair to form a left handed or right handed physical system in the EPR scenario. It is just plain common sense that there is a 50-50 chance in Nature that the pair is created as either left handed or right handed. After averaging many trials, the left and right handed components cancel each other out and go to zero and we are left with -a.b. The same prediction as QM. It is so simple that it is a thing of total beauty.

[FrediFizzx]

As further proof of Lockyer's double translation math error, we will consider just the vector cross product part of his calculation as it is easy to visualize what is going on. Consider two vectors a and b at right angle to each other in the right hand rule and left hand rule. If a is pointing up and b is pointing out of the page then a x b = c points to the right in the right hand system. Likewise a x b = c points to the left for the left hand system by the left hand rule. So it is easy to see that from the right handed perspective that the left handed c will be -c. IOW, a x b --> -(a x b) = (b x a) = -c upon translation. So the cross product part of his C above for the right handed system is,

a x b (RH) = (a_2 b_3 – a_3 b_2) e_1 + (a_3 b_1 – a_1 b_3) e_2 + (a_1 b_2 – a_2 b_1) e_3

And that can be verified here. So the left handed cross product in the left handed system will be,

a x b (LH) = (a_2 b_3 – a_3 b_2) f_1 + (a_3 b_1 – a_1 b_3) f_2 + (a_1 b_2 – a_2 b_1) f_3

Now do the mapping of f_ --> -e_ as Lockyer specified and we get,

b x a (LH from RH perspective) = (a_2 b_3 – a_3 b_2) (-e_1) + (a_3 b_1 – a_1 b_3) (-e_2) + (a_1 b_2 – a_2 b_1) (-e_3)
=
b x a = (-a_2 b_3 + a_3 b_2) (e_1) + (-a_3 b_1 + a_1 b_3) (e_2) + (-a_1 b_2 + a_2 b_1) (e_3)

QED. Now... if Lockyer is correct, there should be an error above. But there is none thus he double mapped his calculation which is shown at the beginning of this thread. It is that simple folks. Lockyer is definitely stuck on stupid. ???

Notice how Lockyer keeps going off-topic by saying Joy has an error instead of admitting to his own math error.

[Rick Lockyer]

You have made it abundantly clear where you have gone off the rails

a x b (RH) = (a_2 b_3 – a_3 b_2) e_1 + (a_3 b_1 – a_1 b_3) e_2 + (a_1 b_2 – a_2 b_1) e_3

And that can be verified here. So the left handed cross product in the left handed system will be,

a x b (LH) = (a_2 b_3 – a_3 b_2) f_1 + (a_3 b_1 – a_1 b_3) f_2 + (a_1 b_2 – a_2 b_1) f_3

Your LH expression has exactly the same coefficient signs as the RH expression. Since these signs come from the basis element product rules which define the orientation of the algebra, you are claiming e and f are the same algebra, no orientation change whatsoever. f_2 f_3 = -f_1 NOT +f_1. This IS the orientation difference. So reality is

a x b (LH) = (-a_2 b_3 + a_3 b_2) f_1 + (-a_3 b_1 + a_1 b_3) f_2 + (-a_1 b_2 + a_2 b_1) f_3

Now do the proper map to the e system f_x -> -e_x. What do you get fool? You get the same thing as you just showed for the RH system.

This is completely consistent with the obvious by inspection demonstration of a sign error found here:

Only an idiot would not be able to glance at this and see the sign error. Stop the BS, tell us why the two minus signs on the left side of the second equation do not cancel each other out. They can't if there is no sign error, but they do. And this is a very clear indication that when properly looked at (from the same orientation as required to be able to add them) RH and LH are equivalent. The only connection to physical screws we have here are to your loose ones.

[FrediFizzx]

Your LH expression has exactly the same coefficient signs as the RH expression.

Of course they are the same. Please pay attention! I said the LH system from the left hand perspective. What I wrote is 100 percent correct. Besides being stuck on stupid, you are stuck in a right handed only perspective. Please show us how to get b x a = -c in the right handed coordinate system from your result for the left handed cross product? You can't. Unless you double translate again. LOL!

[Joy Christian]

***

This is the second day...

... and I am still shaking my head thinking about the colossal stupidity of Lockyer's "argument" above:

The second equation on the left is equal to the first equation on the left, because the two minus signs on the I terms cancel each other out. The sign error is clearly presented by Christian by the fact the two right handed sides are not equal.

He is claiming that since LHS's of the following two equations are the same but RHS's are not, all the standard textbooks on classical mechanics have a "sign error."



or



where are the generators of angular momenta.



***

And, as usual, he is completely ignoring the following references from my earlier posts:

Just to reassure our readers that I am not making the above point up impromptu, let me stress that it has been explained to Lockyer and company literally thousands of times, in many blog posts and published papers, for many years. See, for one example, the following clear-cut paragraph, reproduced from one of my 2010 papers:



PS: I should point out here for those unfamiliar with my work that the above sign ambiguity is taken as two "hidden variable" possibilities in my local-realistic model.

[FrediFizzx]

Yep, when both are viewed in a right handed coordinate system, Lockyer has a left handed screw the same as a right handed screw. Bizarre and absurd!

Joy, he can't even understand the simple cross product demonstation so he will never understand what you are presenting. I'm trying to simplify things for lurkers here so they can easily see the real truth about Lockyer's math error. Which is what this thread is about.

[FrediFizzx]

As further proof of Lockyer's double translation math error, we will consider just the vector cross product part of his calculation as it is easy to visualize what is going on. Consider two vectors a and b at right angle to each other in the right hand rule and left hand rule. If a is pointing up and b is pointing out of the page then a x b = c points to the right in the right hand system. Likewise a x b = c points to the left for the left hand system by the left hand rule. So it is easy to see that from the right handed perspective that the left handed c will be -c. IOW, a x b --> -(a x b) = (b x a) = -c upon translation. So the cross product part of his C above for the right handed system is,

a x b (RH) = (a_2 b_3 – a_3 b_2) e_1 + (a_3 b_1 – a_1 b_3) e_2 + (a_1 b_2 – a_2 b_1) e_3

And that can be verified here. So the left handed cross product in the left handed system will be,

a x b (LH) = (a_2 b_3 – a_3 b_2) f_1 + (a_3 b_1 – a_1 b_3) f_2 + (a_1 b_2 – a_2 b_1) f_3

Now do the mapping of f_ --> -e_ as Lockyer specified and we get,

b x a (LH from RH perspective) = (a_2 b_3 – a_3 b_2) (-e_1) + (a_3 b_1 – a_1 b_3) (-e_2) + (a_1 b_2 – a_2 b_1) (-e_3)
=
b x a = (-a_2 b_3 + a_3 b_2) (e_1) + (-a_3 b_1 + a_1 b_3) (e_2) + (-a_1 b_2 + a_2 b_1) (e_3)

QED. Now... if Lockyer is correct, there should be an error above. But there is none thus he double mapped his calculation which is shown at the beginning of this thread. It is that simple folks. Lockyer is definitely stuck on stupid. ???

Notice how Lockyer keeps going off-topic by saying Joy has an error instead of admitting to his own math error.

Anyways, continuing on with more explanation here, Lockyer wants us to believe that his result of,

(a_2 b_3 – a_3 b_2) e_1 + (a_3 b_1 – a_1 b_3) e_2 + (a_1 b_2 – a_2 b_1) e_3

for the left handed system translated to right handed system will equal b x a = -c which is impossible as it is equal to a x b = c as seen by link I provided above. The correct result is,

b x a = (-a_2 b_3 + a_3 b_2) (e_1) + (-a_3 b_1 + a_1 b_3) (e_2) + (-a_1 b_2 + a_2 b_1) (e_3) = -c

Do the math. Work it out and you will see that I am 100 percent correct. Lockyer double translated in his original presentation and it has him in some kind of weird stuck on stupid brain-lock.

[Rick Lockyer]

Anyways, continuing on with more explanation here, Lockyer wants us to believe that his result of,

(a_2 b_3 – a_3 b_2) e_1 + (a_3 b_1 – a_1 b_3) e_2 + (a_1 b_2 – a_2 b_1) e_3

for the left handed system translated to right handed system will equal b x a = -c which is impossible as it is equal to a x b = c as seen by link I provided above.

I have said all along when you map the left handed to the right handed basis you get the same thing, and this is precisely why Christian made a sign error. So now this is YOUR position, not mine, and Christian has not made a sign error. Unbelievable.

I have tried the pedagogical approach to teach ALL readers something about algebras and their orientation choices. What have Diether and Christian done but throw as much s*** as they possibly can up against the wall in a lame attempt to bury the truth? Hopefully the pedagogical approach was not a waste of time because some readers tried and succeeded to understand it. Diether, it was lost on you because you are mathematically incompetent. Christian is just looking for cover, something for which you do him no favors by providing since you are incompetent.

We can put the pedagogy and all of your s*** aside, and simply focus on these two equations:

Cut the crap, answer two simple questions.

1. Are the left hand sides of both equal?
2. Are the right hand sides of both equal? Obvious answer is no, they differ by a sign

For Christian to have not made some kind of error, the answer to the first question must be no.

So: Christian, Diether, Tom Ray, Michel Fodje, since you are all on record saying there is no sign error, do explain how the answer to question 1 is "no" as you must to justify your position. I am sure this will not happen.

Obviously the two left hand sides are the same because (-1)(-1) = +1, and this is inconsistent with the difference indicated on the right. Diether, now THAT is QED. Time for Christian's club members to apologize.

My work is done here.

[FrediFizzx]

Go ahead and keep making a fool of yourself. This thread is about your math error, Lockyer. Not anyone elses supposed error. Please explain why your original presentation can't produce,

b x a = -c

which is the correct result for a left handed system translated to the right handed coordinate system as anyone can plainly see.