minkwe wrote:Heinera wrote:minkwe wrote:
New challenge for the Bell Test business people, perform the RHS experiment and demonstrate that you get the same results as the LHS. It should be easier since you have just two expectation values to measure.
<< A(a)*[ B(b) + B(b' ) ] >> , << A(a' )*[ B(b) - B(b' ) ] >>
Is it OK if I do it with fragments of small, exploding balls?
If you have the balls to do it, be my guest.
Bell Imposed -0 and +0 Bounds on the CHSH Correlator
91 posts
• Page 2 of 5 • 1, 2, 3, 4, 5
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
minkwe wrote:Heinera wrote:minkwe wrote:
New challenge for the Bell Test business people, perform the RHS experiment and demonstrate that you get the same results as the LHS. It should be easier since you have just two expectation values to measure.
<< A(a)*[ B(b) + B(b' ) ] >> , << A(a' )*[ B(b) - B(b' ) ] >>
Is it OK if I do it with fragments of small, exploding balls?
If you have the balls to do it, be my guest.
No problem, I'll use Joy's.
- Heinera
- Posts: 917
- Joined: Thu Feb 06, 2014 1:50 am
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
Heinera wrote:minkwe wrote:Heinera wrote:minkwe wrote:
New challenge for the Bell Test business people, perform the RHS experiment and demonstrate that you get the same results as the LHS. It should be easier since you have just two expectation values to measure.
<< A(a)*[ B(b) + B(b' ) ] >> , << A(a' )*[ B(b) - B(b' ) ] >>
Is it OK if I do it with fragments of small, exploding balls?
If you have the balls to do it, be my guest.
No problem, I'll use Joy's.
Sorry, mine are not for you.
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
Last month I wrote in Ilja Schmelzer's forum:
In my opinion, the most important contribution of the Joy Christian “exploding balls” experiment is the introduction of a non-arbitrary initial condition rather than preparing particles in a supposedly entangled state.
There is a widespread belief – articulated in this thread by Richard Gill – that quantum mechanics is different from classical mechanics. Despite the failure of theorists and experimentalists to show where the demarcation is, or where the quantum wave function becomes classical, the belief persists that classical behavior “somehow” derives from quantum rules.
The classical experiment turns this belief on its head, in a locally realistic manner, by removing the special conditions required to violate Bell’s inequality by Bell-Aspect and CHSH type experiments. Joy takes his cue from Newton, to “make no hypothesis” toward physical phenomena.
We should see that for every explosion sharing a common time parameter, that time conservation demands negative correlation between hemispheres. (See d'Espagnat's bold type explanation in https://www.scientificamerican.com/medi ... 1_0158.pdf. This will apply every time the explosion is repeated – implying correlation all the way back to the cosmic initial condition, and reinforcing Einstein’s expectation (Geometry and Experience) that two clocks, having once been synchronized, will remain synchronized when brought back into proximity.
If successful, Joy’s experiment will be remembered in history alongside Galileo’s.
In my opinion, the most important contribution of the Joy Christian “exploding balls” experiment is the introduction of a non-arbitrary initial condition rather than preparing particles in a supposedly entangled state.
There is a widespread belief – articulated in this thread by Richard Gill – that quantum mechanics is different from classical mechanics. Despite the failure of theorists and experimentalists to show where the demarcation is, or where the quantum wave function becomes classical, the belief persists that classical behavior “somehow” derives from quantum rules.
The classical experiment turns this belief on its head, in a locally realistic manner, by removing the special conditions required to violate Bell’s inequality by Bell-Aspect and CHSH type experiments. Joy takes his cue from Newton, to “make no hypothesis” toward physical phenomena.
We should see that for every explosion sharing a common time parameter, that time conservation demands negative correlation between hemispheres. (See d'Espagnat's bold type explanation in https://www.scientificamerican.com/medi ... 1_0158.pdf. This will apply every time the explosion is repeated – implying correlation all the way back to the cosmic initial condition, and reinforcing Einstein’s expectation (Geometry and Experience) that two clocks, having once been synchronized, will remain synchronized when brought back into proximity.
If successful, Joy’s experiment will be remembered in history alongside Galileo’s.
- thray
- Posts: 143
- Joined: Sun Feb 16, 2014 6:30 am
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
thray wrote:If successful, Joy’s experiment will be remembered in history alongside Galileo’s.
I wouldn't go that far, Tom.
Besides, my proposed experiment may never be actually performed. The politically powerful Bell Mafia will make sure that it is never actually performed.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
I posted this on RW to warn Jay which the moderators did not let through.
Jay, they are trying to take you into the Bell trap. Don’t fall for it. There isn’t really a 4 x N matrix. It is much more complicated than that. In a real EPR-Bohm type experiment, every row will have only one result and the other 3 will be N/A for not applicable."
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
FrediFizzx wrote:I posted this on RW to warn Jay which the moderators did not let through.Jay, they are trying to take you into the Bell trap. Don’t fall for it. There isn’t really a 4 x N matrix. It is much more complicated than that. In a real EPR-Bohm type experiment, every row will have only one result and the other 3 will be N/A for not applicable."
Jay will not be fooled by them easily. He is new to this stuff so it may take him a while to figure out their game, but eventually he will see it. They are also insisting that Jay considers millions of events when in their latest "loophole-free" experiment they were quite happy to use only 256 events and demanding a Nobel Prize for it.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
***
I think the message I wanted to bring out in the Appendix D of this paper is being obfuscated by the Bell-believers on Retraction Watch with their usual diversionary tactics. So let me reiterate my central message using their own language so that the essential point of my argument becomes transparent enough. I have reproduced below the derivation of the bounds -2 and +2 on the CHSH correlator from Wikipedia. The second line of that three-line derivation is all that is needed to understand my point. That second line is simply an average of the random variable X(a, a', b, b', lambda), which is defined as
X(a, a', b, b', lambda) := A(a, lambda)*B(b, lambda) + A(a, lambda)*B(b', lambda) + A(a', lambda)*B(b, lambda) - A(a', lambda)*B(b', lambda).
Now it is claimed by the Bell-believers --- and especially by Gill --- that X(a, a', b, b', lambda) is just a random variable on the space of all counterfactually possible outcomes that may be observed by Alice and Bob. And, they claim, the bounds of -2 and +2 on the CHSH correlator follows immediately from its average. Well, they indeed seem to be, because the equality between the first and second lines of the derivation below is a strict mathematical identity. But that is just the problem.
Since that equality is a mathematical identity, we can just take the second line as our starting point and ask: What is exactly being averaged in it? Well, what is being averaged is an "event" that cannot possibly exist in any possible physical world, as demonstrated in my paper linked above. X(a, a', b, b', lambda) is a totally fictitious quantity that cannot possibly exist except in some fantasy world, and therefore the bounds of -2 and +2 derived from it are equally fictitious. They are Mickey Mouse!
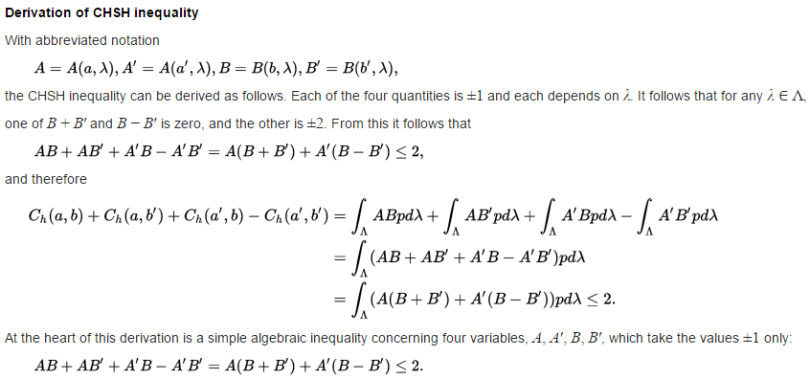
***
I think the message I wanted to bring out in the Appendix D of this paper is being obfuscated by the Bell-believers on Retraction Watch with their usual diversionary tactics. So let me reiterate my central message using their own language so that the essential point of my argument becomes transparent enough. I have reproduced below the derivation of the bounds -2 and +2 on the CHSH correlator from Wikipedia. The second line of that three-line derivation is all that is needed to understand my point. That second line is simply an average of the random variable X(a, a', b, b', lambda), which is defined as
X(a, a', b, b', lambda) := A(a, lambda)*B(b, lambda) + A(a, lambda)*B(b', lambda) + A(a', lambda)*B(b, lambda) - A(a', lambda)*B(b', lambda).
Now it is claimed by the Bell-believers --- and especially by Gill --- that X(a, a', b, b', lambda) is just a random variable on the space of all counterfactually possible outcomes that may be observed by Alice and Bob. And, they claim, the bounds of -2 and +2 on the CHSH correlator follows immediately from its average. Well, they indeed seem to be, because the equality between the first and second lines of the derivation below is a strict mathematical identity. But that is just the problem.
Since that equality is a mathematical identity, we can just take the second line as our starting point and ask: What is exactly being averaged in it? Well, what is being averaged is an "event" that cannot possibly exist in any possible physical world, as demonstrated in my paper linked above. X(a, a', b, b', lambda) is a totally fictitious quantity that cannot possibly exist except in some fantasy world, and therefore the bounds of -2 and +2 derived from it are equally fictitious. They are Mickey Mouse!
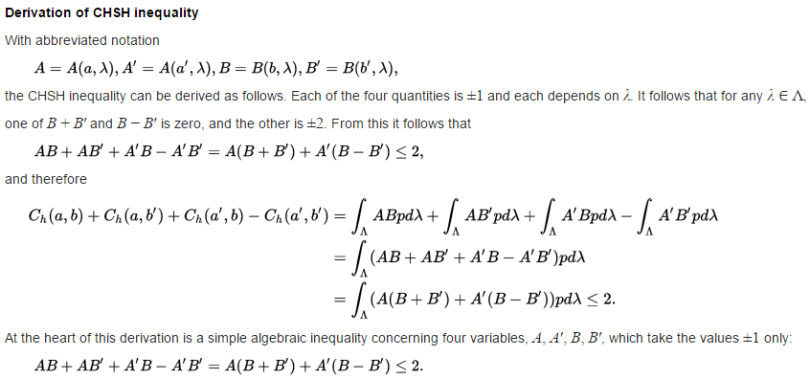
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
If the RHS is impossible, so is the LHS. You are absolutely right Joy.
- minkwe
- Posts: 1441
- Joined: Sat Feb 08, 2014 10:22 am
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
minkwe wrote:
If the RHS is impossible, so is the LHS. You are absolutely right Joy.
It is as simple as that. LHS = RHS is a mathematical identity, which they themselves stress. So they can't claim sanity on the LHS when there is insanity on the RHS.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
Joy Christian wrote:minkwe wrote:
If the RHS is impossible, so is the LHS. You are absolutely right Joy.
It is as simple as that. LHS = RHS is a mathematical identity, which they themselves stress. So they can't claim sanity on the LHS when there is insanity on the RHS.
***
That coupled with the fact that neither QM nor the experiments have ever violated any Bell inequality should have put Bell's theory in the grave a long time ago. And the above highlights why they have never violated a Bell inequality.
.
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
***
My latest post at Retraction Watch in response to Stephen Parrott:
***
My latest post at Retraction Watch in response to Stephen Parrott:
Joy Christian wrote:
Very well, although I have explained my point in detail in the Appendix D of my paper which triggered this discussion ( i.e., this one: https://arxiv.org/abs/1501.03393 ), let me explain my point again using the language traditionally used to prove Bell’s theorem ( see Bell’s famous paper of 1964 ), using the “large N limit” ( i.e., integration ) as well as the usual assumption of “local hidden variables”, as insisted upon by the proponents of Bell’s theorem.
Let me reproduce the key part of the derivation of the bounds -2 and +2 on the CHSH correlator from Bell’s paper of 1964. It involves the mathematical identity we discussed previously, namely E(X) + E(Y) = E(X + Y), and an average of the random variable X(a, a’, b, b’, k) with k as a hidden variable (usually denoted by lambda), which is defined as
X(a, a’, b, b’, k) := A(a, k)*B(b, k) + A(a, k)*B(b’, k) + A(a’, k)*B(b, k) – A(a’, k)*B(b’, k),
where A and B are +1 or -1 and a, a’, b and b’ are possible measurement directions that may be freely chosen by Alice and Bob. The mathematical identity of interest is then
Int_K A(a, k)*B(b, k) rho(k) dk + Int_K A(a, k)*B(b’, k) rho(k) dk + Int_K A(a’, k)*B(b, k) rho(k) dk – Int_K A(a’, k)*B(b’, k) rho(k) dk = Int_K X(a, a’, b, b’ ) rho(k) dk ,
where Int_K denotes integration ( i.e., “large N limit” ) over the space K of hidden variables k.
Let me stress that the above is the standard mathematical identity, frequently used in the derivation of Bell’s theorem, and can be found even in Wikipedia. The RHS of the above identity is simply an “average” of the random variable X(a, a’, b, b’, k) defined above.
Now it is claimed by the followers of Bell that X(a, a’, b, b’, k) is just a random variable on the space of all counterfactually possible outcomes that may be observed by Alice and Bob ( as in my dice example ). And — they claim — the bounds of -2 and +2 on the CHSH correlator follows immediately from its “average” on the RHS. Well, they indeed seem to be, because, as noted, the equality between the LHS and the RHS in the above equation is a strict mathematical identity (as frequently stressed by the followers of Bell), and it is easy to see that the RHS of the equation is bounded by -2 and +2. But that is just the problem.
Since the above equality is a strict mathematical identity, we can just take its RHS as our starting point and ask: What is exactly being averaged in it?
Well, what is being averaged is a quantity that cannot possibly exist in any possible physical world, as demonstrated in my paper linked above. Spacetime events such as B(b) and B(b’ ) are only counterfactually possible measurement results, along two mutually exclusive detector directions, b and b’. Since b and b’ are classical, macroscopic directions, no experimenter has the ability to align his or her detector along both b and b’ simultaneously. Therefore, regardless of any physical theory — classical or quantum — it is impossible for Bob to measure both B(b) and B(b’ ) simultaneously, just as it is impossible for a die to land on 3 and 6 simultaneously. Therefore X(a, a’, b, b’, k), which involves sums like B(b)+B(b’ ), is a totally fictitious quantity that cannot possibly exist except in some fantasy world, and therefore the bounds of -2 and +2 derived from X are equally fictitious. They have nothing whatsoever to do with any possible physical world, classical or quantum. They are merely mathematical curiosities. They by no means rule out any local hidden variable theories. They by no means forbid a strictly local, realistic, and deterministic derivation of the correlation E(a, b) = -a.b. Bell’s so-called “theorem” has no relevance for physics whatsoever.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
My latest reply,
"Can you state the “theorem” in mathematical terms only?"
In response to,
Bell's theorem is NOT a theorem in the clear mathematical sense. Bell's theory is a word statement based on a faulty interpretation of the inequalities. It has never actually been proven so it is not really a theorem at all. And that is what happens sometimes when we try to put words to math. You will always get controversy in situations like that.
.
"Can you state the “theorem” in mathematical terms only?"
In response to,
Q wrote:...Anyway, I do have a question for you all now because half the time it’s not clear to an outsider, if you are all even talking about the same thing.
Bell’s theorem is a theorem, in the clear mathematical sense; does everyone agree on that? The theorem, like all theorems, says “If [hypotheses are true] then [a conclusion follows]”. It doesn’t necessarily say anything about the real world whatsoever; except if you measure the hypotheses to be true or the conclusion to be false, then you could infer something about the other. So that said, the truth of the theorem can be discussed without any mention of real world data; this is the nature and perhaps the beauty, of mathematics. It is then a different question to ask how the theorem applies to the real world. So may I ask all those arguing, in a one word answer (no more), do you believe that the mathematical theorem (again, ignoring anything in the real world) holds true?
Bell's theorem is NOT a theorem in the clear mathematical sense. Bell's theory is a word statement based on a faulty interpretation of the inequalities. It has never actually been proven so it is not really a theorem at all. And that is what happens sometimes when we try to put words to math. You will always get controversy in situations like that.
.
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
***
Here is my latest reply to Q on Retraction watch:
***
Here is my latest reply to Q on Retraction watch:
Joy Christian wrote:
If a theorem is based on a proposition P, but in the proof of that theorem one is forced to use the proposition not-P, then one should immediately recognize that something is seriously wrong. But that is exactly what the followers of Bell are refusing to recognize.
In my comment of “November 12, 2016 at 12:47 am” I have shown that Bell’s theorem starts out assuming Realism (i.e., proposition P) on the LHS of a mathematical identity, but are then forced to use Anti-Realism (i.e., proposition not-P) on the RHS of that identity. Anti-Realism gets surreptitiously smuggled into the proof of their so-called “theorem” when they are forced to use impossible measurement results such as B(b)+B(b’ ) on the RHS.
Bell’s so-called “theorem” is not just a mathematical theorem. It is a claim about whether or not certain correlations observed in Nature are explicable purely locally, and realistically. As such, one is not allowed to smuggle-in Anti-Realism in the proof of Bell’s “theorem.”
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
It looks like you have reached the usual impasse with Heine over at RW. Events or predictions?
The best way to shoot down Bell's theory is by requiring them to demonstrate exactly how the experiments or QM "violate" Bell-CHSH. Then it is easy to show that they are not in fact even using Bell-CHSH but a different inequality.
The best way to shoot down Bell's theory is by requiring them to demonstrate exactly how the experiments or QM "violate" Bell-CHSH. Then it is easy to show that they are not in fact even using Bell-CHSH but a different inequality.
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
FrediFizzx wrote:It looks like you have reached the usual impasse with Heine over at RW. Events or predictions?
The best way to shoot down Bell's theory is by requiring them to demonstrate exactly how the experiments or QM "violate" Bell-CHSH. Then it is easy to show that they are not in fact even using Bell-CHSH but a different inequality.
Here is my latest question to Jay on Retraction Watch:
Joy Christian wrote:
Jay, I do not see entries like A(a)*{ B(b) + B(b’ ) } and A(a’ )*{ B(b) – B(b’ ) } in your dataset. But entries likes those are used by the followers of Bell to prove his “theorem.” Please show me where those entries are — if they are hiding somewhere — either in your description, or in the coincidence-counts recorded between the simultaneously observed detector clicks in the actual experiments (as described by Gill, for example). Thanks.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
Joy Christian wrote:Here is my latest question to Jay on Retraction Watch:Joy Christian wrote:
Jay, I do not see entries like A(a)*{ B(b) + B(b’ ) } and A(a’ )*{ B(b) – B(b’ ) } in your dataset. But entries likes those are used by the followers of Bell to prove his “theorem.” Please show me where those entries are — if they are hiding somewhere — either in your description, or in the coincidence-counts recorded between the simultaneously observed detector clicks in the actual experiments (as described by Gill, for example). Thanks.
***
LOL! But as we know, no matter how concisely we shoot it down, they will never ever accept it. But perhaps this RW episode will make more people aware that Bell's model is junk physics.
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
FrediFizzx wrote:Joy Christian wrote:Here is my latest question to Jay on Retraction Watch:Joy Christian wrote:
Jay, I do not see entries like A(a)*{ B(b) + B(b’ ) } and A(a’ )*{ B(b) – B(b’ ) } in your dataset. But entries likes those are used by the followers of Bell to prove his “theorem.” Please show me where those entries are — if they are hiding somewhere — either in your description, or in the coincidence-counts recorded between the simultaneously observed detector clicks in the actual experiments (as described by Gill, for example). Thanks.
***
LOL! But as we know, no matter how concisely we shoot it down, they will never ever accept it. But perhaps this RW episode will make more people aware that Bell's model is junk physics.
Their (but not Einstein's) local realism demands coincidence "clicks" such as A(a)*{ B(b) + B(b’ ) } and A(a’ )*{ B(b) – B(b’ ) } between the remote detectors of Alice and Bob. If they wish to test their local realism, then they must use coincidence counts involving only these events to demonstrate that Nature violates their local realism.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
minkwe wrote:
If the RHS is impossible, so is the LHS. You are absolutely right Joy.
I wonder why the followers of Bell are unable or unwilling to see this simple logic. They frequently claim that the above is a mathematical identity. If so, and I have no reason to doubt that, then the LHS and RHS are also physically equivalent. It is then clear that the RHS of the above identity involves averaging over two impossible events in spacetime, A(a)*{ B(b) + B(b’ ) } and A(a’ )*{ B(b) – B(b’ ) }. Now neither Einstein’s nor Bell’s local realism demands simultaneous coincidence “clicks” such as A(a)*{ B(b) + B(b’ ) } and A(a’ )*{ B(b) – B(b’ ) }; but the local realism of the followers of Bell does. If the followers of Bell wish to test their local realism, then they must use coincidence-counts involving only these hybrid clicks to demonstrate that Nature violates their local realism. They can’t have it both ways. Either they must admit only coincidence-counts like A(a)*{ B(b) + B(b’ ) } and A(a’ )*{ B(b) – B(b’ ) } in their dataset, or not use such impossible events in the proofs of their “theorem.”
Perhaps if I switch the LHS and RHS of the above identity then they may be able to see what I am talking about:
Even better way to say what I want to say is that what is proved by the followers of Bell is simply this:
It should now be abundantly clear which events are being averaged over and which expectation values are being bounded by -2 and +2.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Bell Imposed -0 and +0 Bounds on the CHSH Correlator
Bell fanatics will never agree to any kind of logic. They are stuck in some kind of fantasy world. I am not sure why it is appropriate to waste time arguing with them. It is really a sad state of affairs for sure.
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
91 posts
• Page 2 of 5 • 1, 2, 3, 4, 5
Return to Sci.Physics.Foundations
Who is online
Users browsing this forum: Baidu [Spider] and 117 guests

