minkwe wrote:So finally you see the problem -- that's progress. But you don't care? Why should you?
Learn to read. If I would see a problem, I would care. But if I see only meaningless, hm, [self-censored] modifications and questions, why should I care?
minkwe wrote:Claiming loophole, loophole. Failing to see that you are applying a double standard to simulations like epr-simple on the one hand, and QM and experimental tests on the other. Either they are all valid or all invalid. Either way, Bell's theorem is toast. If they are all valid, then ep-simple is an effective counterexample. If they are all invalid then Bell's theorem is false, and Bell's inequalities are irrelevant to physics.
Complete nonsense. Bell starts with theoretical assumptions, in particular Einstein causality, and derives an inequality. This inequality is, in principle, open to experimental tests. The ideal test would allow to falsify the assumption of Einstein causality (in the stronger meaning of "causality" supported by Einstein himself).
But the real experiments have, of course, limitations, which have to be considered. A simple one is the detector efficiency loophole, but there are other ones. Up to now, only the detector efficiency loophole has played a role here, simply because all your simulations use it. There is no double standard, simulations which use detector efficiency loopholes are rejected as invalid refutations, and experimental tests with detector efficiency loophole are rejected as experimental refutations of Einstein causality.
But it seems you don't understand the key point how Bell circumvents the necessity for having all outcomes out of the same experiment. It is part of the formula
 = \int A(a,\lambda) B(b,\lambda) \rho(\lambda) d\lambda.)
The probability density
 d\lambda.)
and the functions
 B(b,\lambda))
of this formula describes, in a realistic theory, the state which results from a given preparation procedure. That means, if you use the same preparation procedure, the realistic theory predicts also the same P(a,b). This is the physical meaning of this equation. And that's why you can use the same preparation procedure to measure, in different rounds, P(a,b) for different choices of a and b.
And the simulation has to follow the same scheme - it has to define the functions
, B(b,\lambda))
and the random set which approximates some fixed probability distribution
 d\lambda)
in the preparational part, without any contact with actual values a,b. And only after this a- and b-independent preparation one can compute the P(a,b), P(a,c), P(b,c).
You have noted that if one uses exactly the same sets to compute them, the BI will hold exactly. Instead, if one uses different sets, minor violations are possible, which corresponds to the fact that different subsets of values of
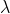
can all approximate the same fixed probability distribution
 d\lambda)
, but not exactly, but only approximately, while the BI are derived assuming
 d\lambda)
exactly. But these are unsystematic rounding errors, and not relevant, with large enough numbers of values they decrease.
The situation is completely different if you choose different
 d\lambda)
to compute P(a,b), P(a,c), resp. P(b,c), or, in other words, some
 d\lambda)
. In this case, there can appear arbitrary large violations of the BI which don't go away with increasing numbers.
minkwe wrote:You should care because Bell's inequality can only be derived if the averages P(a,b), P(a,c) and P(b,c) are measured at exactly the same time on exactly the same set of particle pairs.
Which is simply wrong, Bell has derived it in a different way, using the EPR argument to prove predetermination.
minkwe wrote:the Bell proof, if you actually come to grips with it, falls apart in your hands! There is nothing to it. It’s not just flawed, it’s silly. If you look at the assumptions it made, it does not hold up for a moment. It’s the work of a mathematician, and he makes assumptions that have a mathematical symmetry to them. When you translate them into terms of physical disposition, they’re nonsense. You may quote me on that: the proof of Bell is not merely false but foolish.
Ok, I quote you with this, and the only point of quoting it is to show that what you claim is not merely false but foolish. Which is sufficiently self-evident now for the reader.

