Joy's derivation of the 2*sqrt(2) bound

[FrediFizzx]

So the first original term -A2B2A1B1 after reduction can be rewritten as -A2A1B2B1? Is that correct?

Yes, that is correct.

Ok good. I think I have it all straight now and we are ready to analyze for dependency/independency. I will put it all together in a couple of hours.

[FrediFizzx]

So taking eq. (18) in this paper and squaring the integrand results in the following formula. We have relabelled the A's and B's so easier to check with GAViewer and perhaps easier to follow.
Step 1:
(A1B1 + A1B2 + A2B1 - A2B2) (A1B1 + A1B2 + A2B1 - A2B2) =
A1B1A1B1 + A1B2A1B1 + A2B1A1B1 - A2B2A1B1 + A1B1A1B2 + A1B2A1B2 + A2B1A1B2 - A2B2A1B2 + A1B1A2B1 + A1B2A2B1 + A2B1A2B1 - A2B2A2B1 - A1B1A2B2 - A1B2A2B2 - A2B1A2B2 + A2B2A2B2

And it is obvious that the expansion is correct. Now, the terms in the result can be collected as follows but keeping the A orders and B orders the same.
Step 2:
A1A1B1B1 + A1A1B2B1 + A2A1B1B1 - A2A1B2B1 + A1A1B1B2 + A1A1B2B2 + A2A1B1B2 - A2A1B2B2 + A1A2B1B1 + A1A2B2B1 + A2A2B1B1 - A2A2B2B1 - A1A2B1B2 - A1A2B2B2 - A2A2B1B2 + A2A2B2B2

Then since a bivector squared is -1 we further reduce to;
Step 3:
1 - B2B1 - A2A1 - A2A1B2B1 - B1B2 + 1 + A2A1B1B2 + A2A1 - A1A2 + A1A2B2B1 +1 + B2B1 - A1A2B1B2 + A1A2 + B1B2 +1

Which further reduces to;
Step 4:
4 - A2A1B2B1 + A2A1B1B2 + A1A2B2B1 - A1A2B1B2

We saw earlier that this is the result we want and is verified by GAViewer to be correct and after taking the square root and applying many iterations gives us . Now the original dependency between expectation terms is shown by this;

A1B1 + A1B2 + A2B1 - A2B2

So if an independency is creeping in here, I would say that it has to be in step 2. Otherwise this is a mystery as to how (A1B1 + A1B2 + A2B1 - A2B2) with dependent expectation terms can return since it is mathematically proven that it can't be larger than 2. However, I think Joy claims it is because the original math proof doesn't use bivectors and GA. Joy, please correct me if I am wrong about that.

PS: The reason I think it has to be in Step 2 because we saw earlier without the rearrangement, the result came out to be 2 since the scalar cancelled out.

[Joy Christian]

Now the original dependency between expectation terms is shown by this;

A1B1 + A1B2 + A2B1 - A2B2

So if an independency is creeping in here, I would say that it has to be in step 2. Otherwise this is a mystery as to how (A1B1 + A1B2 + A2B1 - A2B2) with dependent expectation terms can return since it is mathematically proven that it can't be larger than 2. However, I think Joy claims it is because the original math proof doesn't use bivectors and GA. Joy, please correct me if I am wrong about that.

I think the best way to see the difference between the (in)dependent scalar valued functions and the bivector valued functions is to write your Step 4 as follows:

F = 4 - A2A1B2B1 + A2A1B1B2 + A1A2B2B1 - A1A2B1B2 = 4 + [ A1, A2 ] [ B2, B1 ].

Now if A1 and A2 (and likewise B1 and B2) are scalars, then the two commutators vanish, and we get F = 4, so that S = = 2.

But if A1 and A2 (and likewise B1 and B2) are bivectors, then the two commutators do not vanish, each giving a maximum value of 2, so that F = 4 + 4 and S = .

[FrediFizzx]

Now the original dependency between expectation terms is shown by this;

A1B1 + A1B2 + A2B1 - A2B2

So if an independency is creeping in here, I would say that it has to be in step 2. Otherwise this is a mystery as to how (A1B1 + A1B2 + A2B1 - A2B2) with dependent expectation terms can return since it is mathematically proven that it can't be larger than 2. However, I think Joy claims it is because the original math proof doesn't use bivectors and GA. Joy, please correct me if I am wrong about that.

I think the best way to see the difference between the (in)dependent scalar valued functions and the bivector valued functions is to write your Step 4 as follows:

F = 4 - A2A1B2B1 + A2A1B1B2 + A1A2B2B1 - A1A2B1B2 = 4 + [ A1, A2 ] [ B2, B1 ].

Now if A1 and A2 (and likewise B1 and B2) are scalars, then the two commutators vanish, and we get F = 4, so that S = = 2.

But if A1 and A2 (and likewise B1 and B2) are bivectors, then the two commutators do not vanish, each giving a maximum value of 2, so that F = 4 + 4 and S = .

I don't think that quite explains why the rearrangement of A's and B's make the difference. When we had this,

F = 4 - A2B2A1B1 + A2B1A1B2 + A1B2A2B1 - A1B1A2B2 (each term is a rotor; scalar plus bivector)

The scalars cancelled out so we had F = 4 + (bivector terms) which the bivector terms cancel out with many iterations so the result is 2. Rearranging to

F = 4 - A2A1B2B1 + A2A1B1B2 + A1A2B2B1 - A1A2B1B2 (each term is a rotor; scalar plus bivector)

Gives the result.

[Joy Christian]

Now the original dependency between expectation terms is shown by this;

A1B1 + A1B2 + A2B1 - A2B2

So if an independency is creeping in here, I would say that it has to be in step 2. Otherwise this is a mystery as to how (A1B1 + A1B2 + A2B1 - A2B2) with dependent expectation terms can return since it is mathematically proven that it can't be larger than 2. However, I think Joy claims it is because the original math proof doesn't use bivectors and GA. Joy, please correct me if I am wrong about that.

I think the best way to see the difference between the (in)dependent scalar valued functions and the bivector valued functions is to write your Step 4 as follows:

F = 4 - A2A1B2B1 + A2A1B1B2 + A1A2B2B1 - A1A2B1B2 = 4 + [ A1, A2 ] [ B2, B1 ].

Now if A1 and A2 (and likewise B1 and B2) are scalars, then the two commutators vanish, and we get F = 4, so that S = = 2.

But if A1 and A2 (and likewise B1 and B2) are bivectors, then the two commutators do not vanish, each giving a maximum value of 2, so that F = 4 + 4 and S = .

I don't think that quite explains why the rearrangement of A's and B's make the difference. When we had this,

F = 4 - A2B2A1B1 + A2B1A1B2 + A1B2A2B1 - A1B1A2B2 (each term is a rotor; scalar plus bivector)

The scalars cancelled out so we had F = 4 + (bivector terms) which the bivector terms cancel out with many iterations so the result is 2. Rearranging to

F = 4 - A2A1B2B1 + A2A1B1B2 + A1A2B2B1 - A1A2B1B2 (each term is a rotor; scalar plus bivector)

Gives the result.

GAviewer is probably blind to the fact that A's and B's are space-like separated and hence commute. How does it compute the product of four bivectors, say in A2B2A1B1? Does it compute A2B2 first, and then A1B1, and then (A2B2)*(A1B1)? I suspect it must be picking a wrong order somehow in the first expression of F.

[FrediFizzx]

I don't think that quite explains why the rearrangement of A's and B's make the difference. When we had this,

F = 4 - A2B2A1B1 + A2B1A1B2 + A1B2A2B1 - A1B1A2B2 (each term is a rotor; scalar plus bivector)

The scalars cancelled out so we had F = 4 + (bivector terms) which the bivector terms cancel out with many iterations so the result is 2. Rearranging to

F = 4 - A2A1B2B1 + A2A1B1B2 + A1A2B2B1 - A1A2B1B2 (each term is a rotor; scalar plus bivector)

Gives the result.

GAviewer is probably blind to the fact that A's and B's are space-like separated and hence commute. How does it compute the product of four bivectors, say in A2B2A1B1? Does it compute A2B2 first, and then A1B1, and then (A2B2)*(A1B1)? I suspect it must be picking a wrong order somehow in the first expression of F.

You might be right.

Code: Select all

>> A2 B2 A1 B1
ans = 0.29 + -0.26*e2^e3 + -0.54*e3^e1 + -0.74*e1^e2
>> E=(A2 B2)
E = 0.10 + -0.10*e2^e3 + 0.19*e3^e1 + 0.97*e1^e2
>> F=(A1 B1)
F = -0.77 + 0.39*e2^e3 + -0.44*e3^e1 + -0.25*e1^e2
>> E F
ans = 0.29 + -0.26*e2^e3 + -0.54*e3^e1 + -0.74*e1^e2
>> E*F
ans = 0.29 + -0.26*e2^e3 + -0.54*e3^e1 + -0.74*e1^e2
>> E.F
ans = 0.37

Because E F and E*F are the same as doing all 4 at once. If that is the case then getting a result of 2 the first way without rearrangement is just a fluke?

However we get the same kind of result when doing A2A1B2B1. And GAViewer confirms that we get 4(a1 x a2).(b2 x b1) for the scalar part of the whole sum of terms.

[FrediFizzx]

Perhaps what Michel wrote last year will shed some light on this.
viewtopic.php?f=6&t=49&start=160&hilit=Invariance#p2578

Before I take my break however, as concerns Tsirelson's bound:

[1] S = E(a − b) + E(a − b') + E(a' − b) − E(a' − b')
Can be written as
[2] S = f (x) + f (y) + f (z) − f (w), w, x, y, z ∈ [0, 2π], and −1 ≤ f(.) ≤ 1

If where w, x, y and z were independent variables, the upper bound of S would be 4 as we've established elsewhere. But inspection of [1] shows that they are not because we can express w in terms of the other three variables w = y + z -x to get

[3] S = f (x) + f (y) + f (z) − f (y + z − x)

At the extrema of S, the partial derivatives of S are all zero:
f'(x) + f'(y + z − x) = f'(y) − f'(y + z − x) = f'(z) − f'(y + z − x) = 0, therefore y = z and f'(y) = f'(z) = -f'(x). Substituting in [3] we get

[4] Se = f(x) + 2f(y) − f(2y − x)

For even f(.), f'(x) = f'(-x) = f'(y). At the extrema therefore, y = -x and we can reduce [4] further to

[5] Se = 3f(y) - f(3y)

Therefore the maximum of S = cos(a, b) + cos(a, b') + cos(a', b) - cos(a', b') is also the maximum of the function

3cos(y) - cos(3y)

Which is 2 sqrt 2. http://www.wolframalpha.com/input/?i=Ma ... os%283x%29

Like I told you, there is nothing quantum about Tsirelson's bound, nor is any Hilbert space involved.

[Joy Christian]

These are all commuting numbers, so mathematically this is quite a different argument.

Is there any way to tell the GAviewer that A's and B's commute for the first F?

The only difference between the first F and the second F is the assumption [ Ai, Bj ] = 0 that is used in the second F (the first F does not use this assumption).

[FrediFizzx]

These are all commuting numbers, so mathematically this is quite a different argument.

Is there any way to tell the GAviewer that A's and B's commute for the first F?

Well, the point is that it is possible to show a violation with "dependent" terms. It is a subtle thing on exactly what the dependency is.

I don't think GAViewer will do that but I will investigate it further.

[FrediFizzx]

These are all commuting numbers, so mathematically this is quite a different argument.

Is there any way to tell the GAviewer that A's and B's commute for the first F?

Well, the point is that it is possible to show a violation with "dependent" terms. It is a subtle thing on exactly what the dependency is.

Ok, puzzle is solved. You can only get a "violation" of CHSH with dependent expectation terms if the terms are counterfactual. And of course using counterfactual terms is how quantum theory shows a "violation" of CHSH. So once again Joy's model matches the QM predictions of a bound of .

[minkwe]

These are all commuting numbers, so mathematically this is quite a different argument.

Is there any way to tell the GAviewer that A's and B's commute for the first F?

Well, the point is that it is possible to show a violation with "dependent" terms. It is a subtle thing on exactly what the dependency is.

I don't think GAViewer will do that but I will investigate it further.

I don't think this is right. Consider the following: Let be a function of a single variable, any function, defined such that it has range



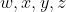
Let us for the moment not care about the domain of the function. But it immediately follows that for 4 independent variables in it's domain , any linear combination of the function over those variables is bounded above by 4 and below by -4:



It turns out that the calculation often performed by experimentalists using experimental expectations, and also that predicted by using quantum mechanics is similar. It is



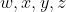
Since we already know that those terms relate to statistically independent measurements, we should conclude that the upper bound is 4 as well. However, the variables in the EPRB scenario are not completely independent. Often the expression is written as:


which is exactly equivalent to


Therefore we have 3 independent variables only. What then is the upper bound for this expression. With a little algebra, we find that the upper bound is also the maximum of the expression



Which corresponds to 2 sqrt 2 when f(x) = cos(x). (http://www.wolframalpha.com/input/?i=Ma ... os%283x%29)

On the flip side, if we know that the terms are counterfactual as in the CHSH or Bell's inequality, then there is more dependence between the terms than just the settings as explained above, and the upper bound is 2 because






where
therefore the expression reduces to



Which factors as


And obviously the upper bound for this expression is 2. This is the CHSH. However, this analysis does not work for experiments and QM because instead of exactly the same functions , we have a different context each time for independent measurements and instead we have






The factorizations do not work, so we are left with only the settings dependency present in the fourth term and must use the previous method to analyze the upper bound, which gives us



In summary:

- Counterfactual dependent terms like in Bell/CHSH gives us
- 4 Independent measurements with 3 independent angle variables gives us a maximum of , which for f(x) = cos(x) is 2 sqrt 2. You can solve this equation to find what settings will give you the maximum values and it turns out to be just the ones used by Bell. But there are many other combinations. See the wolfram alpha link above.
- 4 Completely independent measurements at 4 independent settings, gives us a maximum of 4.
Therefore, "violation" is only possible, if the terms are independent but impossible for terms with the same dependence as in the CHSH.

Note that if the 4 variables 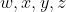are indepependent, even if , we will still have an upper bound of 4.

[Joy Christian]

Counterfactual dependent terms like in Bell/CHSH gives us

This is correct if etc. are the commuting scalar numbers.

But if are non-commuting numbers -- such as the standardized bivectors used in my derivation -- then the bound is , as verified by Fred using GAviewer.

[minkwe]

Counterfactual dependent terms like in Bell/CHSH gives us

This is correct if etc. are the commuting scalar numbers.

But if are non-commuting numbers -- such as the standardized bivectors used in my derivation -- then the bound is , as verified by Fred using GAviewer.

If they are noncommuning then you have a situation more like






Which can not be factorized and left with only the angle dependences, you do indeed get 2 root 2. Non-commutation means the terms must be independent, since they can't be measured simultaneously.

It confirms the conclusion that "violation" is only possible with independent terms.

[FrediFizzx]

If they are noncommuning then you have a situation more like






Which can not be factorized and left with only the angle dependences, you do indeed get 2 root 2. Non-commutation means the terms must be independent, since they can't be measured simultaneously.

It confirms the conclusion that "violation" is only possible with independent terms.

Didn't you mean,





?
Anyways, we know now that QM and Joy's derivation don't actually violate Bell-CHSH. However, I do think that Joy's derivation does match and explain the QM prediction physically.

[Joy Christian]

Counterfactual dependent terms like in Bell/CHSH gives us

This is correct if etc. are the commuting scalar numbers.

But if are non-commuting numbers -- such as the standardized bivectors used in my derivation -- then the bound is , as verified by Fred using GAviewer.

If they are noncommuning then you have a situation more like






Which can not be factorized and left with only the angle dependences, you do indeed get 2 root 2. Non-commutation means the terms must be independent, since they can't be measured simultaneously.

It confirms the conclusion that "violation" is only possible with independent terms.

This is correct too. However, I have always been able to have my cake and eat it too, which, sadly, not many people have understood . What do I mean by that?

Well, in my framework the etc. in the above equations are standardized variables, or standard scores, not the experimentally observed raw scores. I have explained the important distinction in many papers [see, for example, Eqs. (105) to (111) of this paper] so I will not go through it again, but here is the relationship between the two [see Eqs. (7) and (8) of this paper]:

A_i(a, u) = d(a) h_i(a, u) = +/-1 (= commuting scalar number),

where u is the hidden variable, a is the measurement direction, d(a) is a detector bivector, h_i(a, u) is the non-commuting standard score (a bivector), and A_i(a, u) = +/-1 is the actually observed raw score. Since A_i(a, u) are commuting scalar numbers, when naively calculated [as Gill is shown to do in Eqs. (12) and (14) of this paper] the bound appears to be 2. However, when correctly calculated using the standardized variables h_i(a, u), which are non-commuting numbers, the bound is . So here we have a situation where "totally dependent" raw scores A_i(a, u) (which are the same in both E11 and E12 of CHSH) leads to a bound greater than 2.

This of course matches perfectly with the standard experimental computation of the actual correlation, as shown in the derivation of Eq. (B10) in the above paper.

Unfortunately subtleties like these in my work has allowed people like Gill to twist facts and misrepresent my work, either because they are dimwits or dishonest.

PS: Here is a nice pedagogical explanation of the difference between raw scores and standard scores: http://www.gifted.uconn.edu/siegle/rese ... cores.html

[minkwe]

If they are noncommuning then you have a situation more like






Which can not be factorized and left with only the angle dependences, you do indeed get 2 root 2. Non-commutation means the terms must be independent, since they can't be measured simultaneously.

It confirms the conclusion that "violation" is only possible with independent terms.

Didn't you mean,





?

Yes Fred that is exactly what I meant.

[FrediFizzx]

So now that we are done with Joy's derivation, let's take a look at the QM derivation.

https://en.wikipedia.org/wiki/Quantum_m ... prediction

I think from that we can get the following "CHSH" type expression for 1/2 spin quantum objects.



Then we can show that (a-b')+(a'-b)-(a-b) = a'-b' so that we have the situation that Michel demonstrated.

And actually Joy's model could be done this way also since his model predicts E(a, b) = -a.b.

[Joy Christian]

So now that we are done with Joy's derivation, let's take a look at the QM derivation.

https://en.wikipedia.org/wiki/Quantum_m ... prediction

I think from that we can get the following "CHSH" type expression for 1/2 spin quantum objects.



Then we can show that (a-b')+(a'-b)-(a-b) = a'-b' so that we have the situation that Michel demonstrated.

And actually Joy's model could be done this way also since his model predicts E(a, b) = -a.b.

Fred, Please see Eq. (5) of my Reply to Critics.

PS: Also, my original 2007 derivation of the bound is similar to the one in this Wikipedia article. I had all of the key derivations already done in 2007.

[FrediFizzx]

So now that we are done with Joy's derivation, let's take a look at the QM derivation.

https://en.wikipedia.org/wiki/Quantum_m ... prediction

I think from that we can get the following "CHSH" type expression for 1/2 spin quantum objects.



Then we can show that (a-b')+(a'-b)-(a-b) = a'-b' so that we have the situation that Michel demonstrated.

And actually Joy's model could be done this way also since his model predicts E(a, b) = -a.b.

Fred, Please see Eq. (5) of my Reply to Critics.

PS: Also, my original 2007 derivation of the bound is similar to the one in this Wikipedia article. I had all of the key derivations already done in 2007.

Yes. But the point I was making is how Michel's demonstration applies to the QM derivation and to yours.



IOW, the dependency in the (a'-b') = y+z-x

[FrediFizzx]

Man, these Codecogs tex graphics are really coming in slow for me.