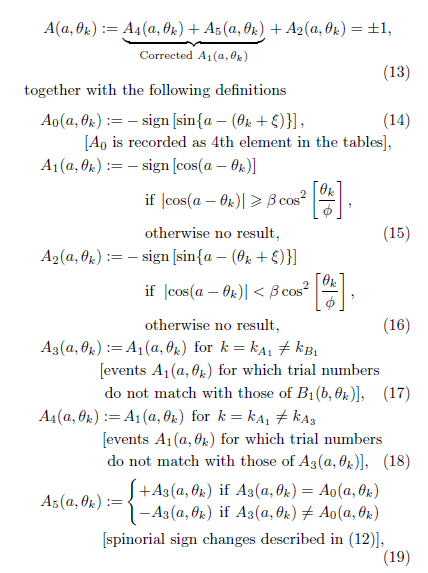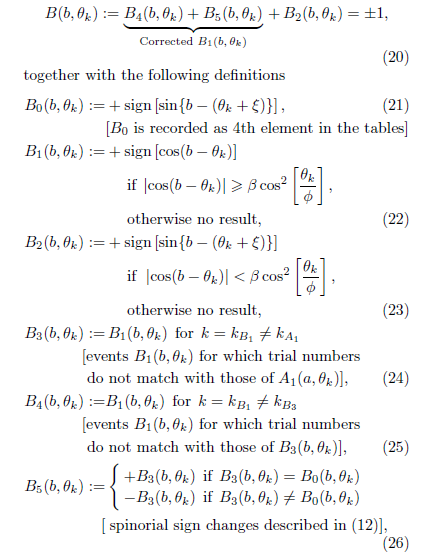Coming Soon!

[Joy Christian]

I'm not going by your rules. Take it or leave it. I'll do whatever I need to do to show that your code is nothing but a bunch of confusing nonsense. Now, with that said, let's see your latest innovation in confusion.

On the contrary, Fred's code is one of the most beautiful demonstrations that Bell's "theorem" is nothing but a piece of junk, and whoever believes in it can't possibly be very smart.
.

[FrediFizzx]

.. I'm not going by your rules. Take it or leave it. I'll do whatever I need to do to show that your code is nothing but a bunch of confusing nonsense. Now, with that said, let's see your latest innovation in confusion.

So, John admits that he can't make a non-local model now without making his old strawman. Actually, this is a face that cares not about what you do. We have already won the battle and you don't matter.
.

[jreed]

.. I'm not going by your rules. Take it or leave it. I'll do whatever I need to do to show that your code is nothing but a bunch of confusing nonsense. Now, with that said, let's see your latest innovation in confusion.

So, John admits that he can't make a non-local model now without making his old strawman. Actually, this is a face that cares not about what you do. We have already won the battle and you don't matter.
.

So I guess you've run out of ways to hide that pesky non-locality. If you don't have anything else, I must have won the battle. Of course I await further attempts. The ball is in your court.

[FrediFizzx]

.. I'm not going by your rules. Take it or leave it. I'll do whatever I need to do to show that your code is nothing but a bunch of confusing nonsense. Now, with that said, let's see your latest innovation in confusion.

So, John admits that he can't make a non-local model now without making his old strawman. Actually, this is a face that cares not about what you do. We have already won the battle and you don't matter.
.

So I guess you've run out of ways to hide that pesky non-locality. If you don't have anything else, I must have won the battle. Of course I await further attempts. The ball is in your court.

.

[gill1109]

I'm not going by your rules. Take it or leave it. I'll do whatever I need to do to show that your code is nothing but a bunch of confusing nonsense. Now, with that said, let's see your latest innovation in confusion.

On the contrary, Fred's code is one of the most beautiful demonstrations that Bell's "theorem" is nothing but a piece of junk, and whoever believes in it can't possibly be very smart.

Fred’s code is unnecessarily complex. However, what it actually does is pretty simple. It is easy to check that changing Bob’s setting can change Alice’s outcome, and vice versa too. I’m looking forward to playing with Joy’s version, written in R.

[FrediFizzx]

I'm not going by your rules. Take it or leave it. I'll do whatever I need to do to show that your code is nothing but a bunch of confusing nonsense. Now, with that said, let's see your latest innovation in confusion.

On the contrary, Fred's code is one of the most beautiful demonstrations that Bell's "theorem" is nothing but a piece of junk, and whoever believes in it can't possibly be very smart.

Fred’s code is unnecessarily complex. However, what it actually does is pretty simple. It is easy to check that changing Bob’s setting can change Alice’s outcome, and vice versa too. I’m looking forward to playing with Joy’s version, written in R.

More nonsense of course. The code is not very complex at all and what it does is kill your lame junky theory.
.

[FrediFizzx]

Hmm... So John, 99.998 percent local is laughable? It is we who are laughing at the Bell fanatics. Unfortunately, I lost that calculation and can't remember how I did it. But no fear, I have one now that is almost just as good that I have narrowed down the possibilities in it.

https://www.wolframcloud.com/obj/fredif ... al-calc.nb Scroll to the end.

So, we are for sure about 99.5 percent local with proof. I will eventually figure out how to narrow it down even more.

The direct files. Scroll to the end.

EPRsims/newCS-24-local-calc.pdf
EPRsims/newCS-24-local-calc.nb

Yeah baby, we are sooooooo local you Bell fanatics will be crying again soon.

I've narrowed this down further by checking each possibility for a change in A. Out of the possibilities, we have 19 events where A changed. Which gives us 99.81 percent local for those that reject the spinorial sign changes as the reason which gives us 100 percent local. And which the Bell fanatics can do NOTHING about it so cry baby cry!! You guys are finished!
.

[gill1109]

I'm not going by your rules. Take it or leave it. I'll do whatever I need to do to show that your code is nothing but a bunch of confusing nonsense. Now, with that said, let's see your latest innovation in confusion.

On the contrary, Fred's code is one of the most beautiful demonstrations that Bell's "theorem" is nothing but a piece of junk, and whoever believes in it can't possibly be very smart.

Fred’s code is unnecessarily complex. However, what it actually does is pretty simple. It is easy to check that changing Bob’s setting can change Alice’s outcome, and vice versa too. I’m looking forward to playing with Joy’s version, written in R.

More nonsense of course. The code is not very complex at all and what it does is kill your lame junky theory.
.

That's a matter of opinion, Fred. Write us some transparent pseudo-code, or teach yourself Python and write your algorithm in Python, then we can start talking again.

.. . but you don't do that because you can't ... or you can, but you know that if you did, the non-locality would be painfully obvious.

The only person you are fooling is yourself (and maybe also poor Joy).

[jreed]

Hmm... So John, 99.998 percent local is laughable? It is we who are laughing at the Bell fanatics. Unfortunately, I lost that calculation and can't remember how I did it. But no fear, I have one now that is almost just as good that I have narrowed down the possibilities in it.

https://www.wolframcloud.com/obj/fredif ... al-calc.nb Scroll to the end.

So, we are for sure about 99.5 percent local with proof. I will eventually figure out how to narrow it down even more.

The direct files. Scroll to the end.

EPRsims/newCS-24-local-calc.pdf
EPRsims/newCS-24-local-calc.nb

Yeah baby, we are sooooooo local you Bell fanatics will be crying again soon.

I've narrowed this down further by checking each possibility for a change in A. Out of the possibilities, we have 19 events where A changed. Which gives us 99.81 percent local for those that reject the spinorial sign changes as the reason which gives us 100 percent local. And which the Bell fanatics can do NOTHING about it so cry baby cry!! You guys are finished!
.

Good! I thought you were through and the fun was all over. Now there's a new notebook to simplify and demystify.

[FrediFizzx]

On the contrary, Fred's code is one of the most beautiful demonstrations that Bell's "theorem" is nothing but a piece of junk, and whoever believes in it can't possibly be very smart.

Fred’s code is unnecessarily complex. However, what it actually does is pretty simple. It is easy to check that changing Bob’s setting can change Alice’s outcome, and vice versa too. I’m looking forward to playing with Joy’s version, written in R.

More nonsense of course. The code is not very complex at all and what it does is kill your lame junky theory.
.

That's a matter of opinion, Fred.

Nope! It is a matter of fact now. What don't you get about being 99.81 percent local and 100 percent local with spinorial sign changes? You are finished! Time to get real, get over it and move on!
.

[FrediFizzx]

Hmm... So John, 99.998 percent local is laughable? It is we who are laughing at the Bell fanatics. Unfortunately, I lost that calculation and can't remember how I did it. But no fear, I have one now that is almost just as good that I have narrowed down the possibilities in it.

https://www.wolframcloud.com/obj/fredif ... al-calc.nb Scroll to the end.

So, we are for sure about 99.5 percent local with proof. I will eventually figure out how to narrow it down even more.

The direct files. Scroll to the end.

EPRsims/newCS-24-local-calc.pdf
EPRsims/newCS-24-local-calc.nb

Yeah baby, we are sooooooo local you Bell fanatics will be crying again soon.

I've narrowed this down further by checking each possibility for a change in A. Out of the possibilities, we have 19 events where A changed. Which gives us 99.81 percent local for those that reject the spinorial sign changes as the reason which gives us 100 percent local. And which the Bell fanatics can do NOTHING about it so cry baby cry!! You guys are finished!
.

Good! I thought you were through and the fun was all over. Now there's a new notebook to simplify and demystify.

And..., What don't you get about being 99.81 percent local and 100 percent local with spinorial sign changes? You are finished also!

There is nothing at all mysterious about the code. I will post another explanation soon.
.

[Joy Christian]

The only person you are fooling is yourself (and maybe also poor Joy).

The only intellectually poor bunch in this forum are those who believe in the validity of Bell's so-called "theorem" despite its manifest fruitcake-ness: https://arxiv.org/pdf/1704.02876.pdf.
.

[FrediFizzx]

John, for some reason thinks the Mathematica code for the simulation is mysterious. Here is another simple explanation.
Nothing really mysterious about the A and B Do-loops except we have a splitter that directs the events greater than the HV to an output stream and those events less than the HV to another.

outA1=DeleteCases[A12,{_,0,_,_}]; (*Split into outA1 and outA2*)
outA2=DeleteCases[A22,{_,0,_,_}];

outB1=DeleteCases[B12,{_,0,_,_,_}]; (*Split into outB1 and outB2*)
outB2=DeleteCases[B22,{_,0,_,_,_}];

Then for the A side we have trial number matching that selects events in outA1 to go to listA3 if the events don't match.

listA3=Select[outA1,Intersection[{#[[3]]},Subscript[k, A1]]!={#[[3]]}&]; (Completely local)

Then outA1 goes to outA4 that don't match listA3 trial number-wise. IOW, outA4 is the other part of outA1.

outA4=Select[outA1,Intersection[{#[[3]]},tna]!={#[[3]]}&]; (Completely local)

Then the next part of the A side does the spinorial sign changes from listA3 and that goes to outA5.

Do[If[listA3[[i]][[2]]==listA3[[i]][[4]],\[Delta]=0,\[Delta]=1];
If[\[Delta]==0,ssca[[i]]=1,ssca[[i]]=-1]; (*spinorial sign change*) (Completely local)
outA5[[i]]={listA3[[i]][[1]],ssca[[i]]*listA3[[i]][[2]],listA3[[i]][[3]],listA3[[i]][[4]]},{i,M1}]

Then the next part puts it all together and sorts by trial number to outA.

outA=Sort[Catenate[{outA2,outA4,outA5}],#1[[3]]<#2[[3]]&]; (*Combine lists and sort*) (Completely local)

Then from outA we extract the angle for a and the outcome for A to go to the Analysis Section.

a1= outA[[All,1]]; (*These results are what Alice observes as defined in Eq.(??)*)
A = outA[[All,2]];

The B side is exactly the same except replace all the A's and a's with B's and b's. Doesn't look mysterious at all. So, where's the beef?
.

[jreed]

You left out some important steps that lead up to the non-locality. I'll see if I can make my objection clearer. I'll be back.

[FrediFizzx]

You left out some important steps that lead up to the non-locality. I'll see if I can make my objection clearer. I'll be back.

Nothing is left out. The only thing that leads to what you think are non-localities is the spinorial sign changes. But it turns out we would still be about 99.81 percent local. So, guess what? Your 0.19 percent non-locality is pretty insignificant. Of course we are 100 percent with the local spinorial sign changes. Time to face reality, John. Bell and Gill's theories are junk.
.

[jreed]

You left out some important steps that lead up to the non-locality. I'll see if I can make my objection clearer. I'll be back.

Here is the code with my comments:

I left out the code that generates the trial data There are 10 trials which are
shown below, 10 total for Alice (A1 and A2) and 10 for Bob(B1 and B2):
Each trial is in the format: {detector angle, detector1 value, trial# detector2 value}

m=10;

outA1
{{194,1,1,-1},{82,-1,2,1},{275,-1,3,1},{297,1,5,1},{203,-1,6,-1},{155,1,7,1},{304,-1,8,-1}}

outA2
{{48,1,4,1},{190,1,9,1},{312,1,10,1}}
Alice has 7 “good” trials and 3 “failed” trials.

outB1
{{145,-1,1,1},{108,1,2,-1},{46,-1,3,1},{0,-1,4,-1},{277,-1,6,1},{156,-1,7,-1},{182,1,8,-1},{25,-1,9,1},{234,-1,10,1}}
outB2
{{171,1,5,1}}
Bob has 9 “good” trials and 1 “failed” trial

Keep the failed trial numbers for Alice (4, 9, 10) and for Bob (5) in mind.

********Begin Fred’s magic code************
Matching Events Observed by Alice and Bob using Trial Numbers
kb1=outA1[[All,3]]; (*Two lists of only trial numbers used for matching*)
ka1=outB1[[All,3]];
Local Detection Analysis of the Events Observed by Alice
listA3=Select[outA1,Intersection[{#[[3]]},ka1]!={#[[3]]}&];
listA3
{{297,1,5,1}}
Intersection has generated a list consisting of Alice’s trials with
numbers matching Bob’s failed trials (in this case only one, trial 5)
called listA3.

M1=Length[listA3];
tna=listA3[[All,3]];
outA4=Select[outA1,Intersection[{#[[3]]},tna]!={#[[3]]}&];
outA5=Table[{0,0,0,0},M1];
ssca=ConstantArray[0,M1];

This Do-loop does the following operations:
For each trial in listA3, if Alice’s detector1 equals detector2, no action is
taken else the sign of Alice’s detector1 is flipped.
This operation is carried out on trial numbers where Bob had a
failed trial. This introduces a non-locality, since information from
Bob’s trials are used to change Alice’s data.

Do[If[listA3[[i]][[2]]==listA3[[i]][[4]],δ=0,δ=1];
If[δ==0,ssca[[i]]=1,ssca[[i]]=-1]; (*spinorial sign change*)
outA5[[i]]={listA3[[i]][[1]],ssca[[i]]*listA3[[i]][[2]],listA3[[i]][[3]],listA3[[i]][[4]]},{i,M1}]

The results of the changed trial (in this case trial 5) are combined with the
unchanged data. This trial wasn’t changed since detector1=detector2.

outA=Sort[Catenate[{outA2,outA4,outA5}],#1[[3]]<#2[[3]]&];
outA5
{{297,1,5,1}}
(*Combine lists *)
a1= outA[[All,1]]; (*These results are what Alice observes as defined in Eq.(??)*)
A = outA[[All,2]];

Local Detection Analysis of the Events Observed by Bob
The same sequence of events is now done for Bob’s trials,
Using Alice’s failed trial numbers.

listB3=Select[outB1,Intersection[{#[[3]]},kb1]!={#[[3]]}&];
M2=Length[listB3];
tnb=listB3[[All,3]];
outB4=Select[outB1,Intersection[{#[[3]]},tnb]!={#[[3]]}&];
outB5=Table[{0,0,0,0},M2];
sscb=ConstantArray[0,M2];
Do[If[listB3[[i]][[2]]==listB3[[i]][[4]],δ=0,δ=1];
If[δ==0,sscb[[i]]=1,sscb[[i]]=-1]; (*spinorial sign change*)outB5[[i]]={listB3[[i]][[1]],sscb[[i]]*listB3[[i]][[2]],listB3[[i]][[3]],listB3[[i]][[4]]},{i,M2}]

Here are the input and output lists from this do loop. Alice’s failed trial numbers,
4, 9, and 10:

listB3
outB5
{{0,-1,4,-1},{25,-1,9,1},{234,-1,10,1}}
{{0,-1,4,-1},{25,1,9,1},{234,1,10,1}}

Now two signs have been flipped in Bob’s data, controlled by Alice’s failed
trials.

outB=Sort[Catenate[{outB2,outB4,outB5}],#1[[3]]<#2[[3]]&]; (*Combine lists and sort*)
b1= outB[[All,1]]; (*These results are what Bob observes as defined in Eq.(??)*)
B = outB[[All,2]];

**************End Fred’s magic code********************

The two do loops above are all that is needed to carry out this
operation. That’s what I programmed up to simplify Fred’s
code and carry out the exact same process. All the extra work
involved in selecting certain observations, done with Intersection,
then doing the do-loop on these selected observations and finally
combining them is not necessary, and makes the program much
more complex than necessary. Maybe that’s desirable if
a magic program is wanted.

[FrediFizzx]

.. This Do-loop does the following operations:
For each trial in listA3, if Alice’s detector1 equals detector2, no action is
taken else the sign of Alice’s detector1 is flipped.
This operation is carried out on trial numbers where Bob had a
failed trial. This introduces a non-locality, since information from
Bob’s trials are used to change Alice’s data.

What was the information from Bob's trials that was used?
.

[Joy Christian]

.. This Do-loop does the following operations:
For each trial in listA3, if Alice’s detector1 equals detector2, no action is
taken else the sign of Alice’s detector1 is flipped.
This operation is carried out on trial numbers where Bob had a
failed trial. This introduces a non-locality, since information from
Bob’s trials are used to change Alice’s data.

What was the information from Bob's trials that was used?

The red-colored sentences of John Reed are pure stupidity on his part. There is no other name for it. Trial numbers are shared between Alice and Bob. They are part of the hidden variables, or common causes, or initial states of the singlet system. Sharing trial numbers, or even the entire hidden variable set of functions does not violate locality. Because trial numbers originate in the overlap of the backward lightcones of Alice and Bob. They are part of the shared information between Alice and Bob. To call sharing of trial numbers "nonlocality" is laughable.

Also, there is only one detector for Alice and one detector for Bob in the code. There are no "detector1" and "detector2" in the code for Alice or Bob.


.

[gill1109]

.. This Do-loop does the following operations:
For each trial in listA3, if Alice’s detector1 equals detector2, no action is
taken else the sign of Alice’s detector1 is flipped.
This operation is carried out on trial numbers where Bob had a
failed trial. This introduces a non-locality, since information from
Bob’s trials are used to change Alice’s data.

What was the information from Bob's trials that was used?

The information used was that Bob had a failed trial. That fact depends on his setting as well as on the hidden variable.

The red-colored sentences of John Reed are pure stupidity on his part. There is no other name for it. Trial numbers are shared between Alice and Bob. They are part of the hidden variables, or common causes, or initial states of the singlet system. Sharing trial numbers, or even the entire hidden variable set of functions does not violate locality. Because trial numbers originate in the overlap of the backward lightcones of Alice and Bob. They are part of the shared information between Alice and Bob. To call sharing of trial numbers "nonlocality" is laughable.

Joy, now you are being exceptionally stupid. Trial numbers connect the trials on each side. The information being shared is whether or not Alice and Bob experienced “failure” which is determined by their settings in combination with the already shared hidden variable.

Fred’s code is so complex that neither Fred nor Joy understand what it does!

[Joy Christian]

.. This Do-loop does the following operations:
For each trial in listA3, if Alice’s detector1 equals detector2, no action is
taken else the sign of Alice’s detector1 is flipped.
This operation is carried out on trial numbers where Bob had a
failed trial. This introduces a non-locality, since information from
Bob’s trials are used to change Alice’s data.

What was the information from Bob's trials that was used?

The information used was that Bob had a failed trial. That fact depends on his setting as well as on the hidden variable.

The red-colored sentences of John Reed are pure stupidity on his part. There is no other name for it. Trial numbers are shared between Alice and Bob. They are part of the hidden variables, or common causes, or initial states of the singlet system. Sharing trial numbers, or even the entire hidden variable set of functions does not violate locality. Because trial numbers originate in the overlap of the backward lightcones of Alice and Bob. They are part of the shared information between Alice and Bob. To call sharing of trial numbers "nonlocality" is laughable.

Joy, now you are being exceptionally stupid. Trial numbers connect the trials on each side. The information being shared is whether or not Alice and Bob experienced “failure” which is determined by their settings in combination with the already shared hidden variable.

Fred’s code is so complex that neither Fred nor Joy understand what it does!

Don't make things up to back up your stupidity.

To begin with, there is no failure of any trial. Neither Alice nor Bob "experiences" failure of trials. All particles are detected. This is not a data rejection or detection loophole model.

Secondly, there is no setting dependence in what Fred is doing in the code. None whatsoever. Only trial numbers are matched once, just as they are in any actual experiment.

Fred's code is exceedingly simple to understand. Moreover, everything is completely transparent from the analytical prescription, which is exactly what Fred is following in the code:



.