Justo wrote:minkwe wrote:Question for you then. Does the validity of the statement "
according to quantum mechanics, measurement of
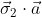 must yield
must yield the value -1 and vice versa. " depend on what measurement was actually made?
No, it does not.
So you agree that after the experiment, in which a different measurement was "in fact" made, by Bob, the statement "
according to quantum mechanics, measurement of
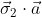 must yield
must yield the value -1 and vice versa. " is still valid. If that is not the definition of counterfactual definiteness, then you don't know what counterfactual definiteness means.
Let us say that P= "Experiment X is performed" and Q=" Result Y is obtained". Then the implication

is not a counterfactual conditional irrespective of P being actually performed or not.
The statement

is a conditional statement. Nobody is suggesting that it is a counterfactual statement. It only becomes counterfactual in the specific context in which

is fact and it is no longer possible for
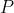
to be true. Counterfactual Definiteness means the statement

is valid and
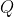
as a result of
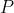
is definite even in the context in which
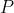
is counterfactual. If you disagree, please provide your definition.
minkwe wrote:please explain the basis for factoring within the integral as Bell does?
The mathematical operations on the right side have nothing to do with counterfactual definiteness. They are mathematical operations and have nothing to do with the way the experiment was performed or is supposed to be performed.
You didn't answer the question. You just made an empty proclamation that is unfounded. What is the basis for factoring? Within the integral, we have AB - BC and then it is factored into AB(AC-1). AB corresponds to the result if measurements A & B are performed together (note that only two measurements can ever be performed together. AC corresponds to the result if measurements A & C are performed together.
Therefore it should be obvious to anyone that AC is counterfactual to AB. If AB was measurement, then AC was not measured and could no longer be measured. Yet you place AB and AC side by side, and perform the factoring to obtain AB(AC-1). This is an assumption of counterfactual definiteness.
All that is assumed is that
=\int d\lambda A(a,\lambda)B(b,\lambda))
, the left side is an experimental result or is supposed to be one. The right side is its mathematical expression. Once you assume this, you can transform the right side with whatever legal mathematical operation without changing its physical meaning.
Sorry, this is just wrong.
gill1109 wrote:Suppose a, b, c = +/-1. Then ab(ac - 1) = bc - ab, but in your rendition of Bell, Bell would have ab - ac.
Well spotted, Michel! This generates a sign error and “ac” instead of “bc”. But in the next displayed formula he has taken an absolute value and also corrected the “ac” to “bc” error. I believe that his final result is OK.
I suspect that this was a typo...
The typo was mine. There should be no minus in front of the second expression. I'm focused on the factoring not the sign.

