Thoughts about Bell, Bohm, Christian, et al.

[minkwe]

A counterexample would be a counterexample even if it would not have any relation to Nature. And the conditions which the counterexample has to fulfill to be a counterexample are defined and fixed forever by Bell's theorem. Pure mathematics, no Nature involved.

I'm afraid you've been deceived, or have not read the relevant papers carefully. I'll be happy to go through page by page with you and see if at the end you still believe Bell's theorem (that's assuming you have an open mind). If you are right and I'm wrong, maybe you can convince me in the process. How about that? Confident enough in your belief? I am in mine, and I'm ready to back it up. Are you?

http://www.drchinese.com/David/Bell_Compact.pdf

[Schmelzer]

I'm afraid you've been deceived, or have not read the relevant papers carefully. I'll be happy to go through page by page with you and see if at the end you still believe Bell's theorem (that's assuming you have an open mind). If you are right and I'm wrong, maybe you can convince me in the process. How about that? Confident enough in your belief? I am in mine, and I'm ready to back it up. Are you?

"Deceived" sounds inappropriate, nobody has even tried to teach me, and certainly nobody has deceived me. Of course Bell's book has strongly influenced me. But I have also developed my own ideas about this.

Ok, let's go page by page. I would not name what I have a "belief", so the question of "confident enough" I would reject as nonsensical. But, given that I can use and use the violation of Bell's inequality as a powerful argument against the mainstream, in favour of a hidden preferred frame, I will, of course, try hard to defend it.

There have been a lot of "conversions" based on arguments during my life, educated as a communist I became a democrat and later an anarcho-capitalist ("deceived" by Friedman's "machinary of freedom"). And there already was a similar point: Some guys have claimed something about tunneling speeds being faster than light - group velocities and this. I had used this initially - but then I have received a mail where someone explained me shortly that this is nonsense. I looked at this more careful, and, indeed, agreed that this is nonsense, and no longer mention this. In this sense, there already is a precedent, you have a chance.

[FrediFizzx]

Hopefully this will be a good discussion. Reminds me of the old days on the sci.physics UseNet group when Ilja and Bilge had some pretty good discussions. I will try to stay out of it unless I can add something constructive.

[minkwe]

Okidoki:
The paper is dealing with a pair of spin 1/2 particles moving in opposite directions such that measurements can be made on them yielding +1 or -1. If measured along the same axis on both arms, the results must be opposite.

This is summarized mathematically in Equation (1)?

A(a,λ) = ±1, B(a, λ) = ±1 (1)

Where lambda is a "more complete specification" of whatever it is that is responsible for the outcomes.
Note, that equation (1) applies to every theory, including QM. We haven't imposed any restrictions on lambda at this point. Lambda could be a non-local mechanism or anything you like. But because we start the discussion saying the results are ±1, on either side, then equation (1) is universally true by definition.

Do you have any problem with my summary presentation up to this point. If you do, please complain loudly. If this is all good with you, could you please tell me what you think equation (2) represents.

[Joy Christian]

A(a,λ) = ±1, B(a, λ) = ±1 (1)

Lambda could be a non-local mechanism or anything you like.

I do not wish to interrupt, but you have a typo in your eq. (1). B should only depend on b, not a.

Also, I do not understand what you mean by your sentence I have quoted. Although lambda can be anything, the expressions for A and B are manifestly local. A does not depend on either b or B, and likewise B does not depend on either a or A, regardless of what lambda is. This makes the outcomes A and B in (1) manifestly local.

Moreover (and this is my main complaint against Bell), one simply cannot define functions like in eq. (1) without specifying the co-domains of the functions. What is defined in (1) is mathematically ill-defined. One must carefully define at least what the domains of the functions A and B are, and what their co-domains are (or is).

[Schmelzer]

Okidoki:
The paper is dealing with a pair of spin 1/2 particles moving in opposite directions such that measurements can be made on them yielding +1 or -1. If measured along the same axis on both arms, the results must be opposite.

This is summarized mathematically in Equation (1)?

A(a,λ) = ±1, B(a, λ) = ±1 (1)

Where lambda is a "more complete specification" of whatever it is that is responsible for the outcomes.
Note, that equation (1) applies to every theory, including QM.

No, it applies only to a class of theories named local realistic. QM is not realistic (that means, it does not specify ) nor local (in interpretations which have a collapse). That QM is not a theory of this type is written de facto explicitly by the open reference to the EPR criterion of reality and supporting the EPR conclusion that QM is incomplete, and a more complete description will be of this type:

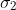
Since we can predict in advance the result of measuring any chosen component of , by previously measuring the same
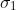
component of , it follows that the result of any such measurement must actually be predetermined. Since the initial quantum mechanical wave
function does not determine the result of an individual measurement, this predetermination implies the possibility of a more complete specification of
the state.
Let this more complete specification be effected by means of parameters

We haven't imposed any restrictions on lambda at this point. Lambda could be a non-local mechanism or anything you like. But because we start the discussion saying the results are ±1, on either side, then equation (1) is universally true by definition.

It isn't, because it specifies a dependence. It differs, for example, from
A(a,b,λ) = ±1, B(a,b, λ) = ±1
that it does not allow a dependence on b of A, and on a of B.

Do you have any problem with my summary presentation up to this point. If you do, please complain loudly. If this is all good with you, could you please tell me what you think equation (2) represents.

Done loud enough. Anyway: Formula (2) already fixes the other point, which appears important here, that does not depend nor on a, nor on b. This has not been mentioned in the text itself, because it has been considered as trivial - last but not least, it was clearly said that we talk about a predetermination of all measurement outcomes (following the EPR argument). The superdeterminism loophole is simply ignored here.

Moreover (and this is my main complaint against Bell), one simply cannot define functions like in eq. (1) without specifying the co-domains of the functions. What is defined in (1) is mathematically ill-defined. One must carefully define at least what the domains of the functions A and B are, and what their co-domains are (or is).

I think the domains and the codomain are defined sufficiently clear. This is a physics paper, not a mathematical one, thus, one has to take into account that the requirements for formal mathematics are lower, but once it is simple, even trivial, to recover the missing formalism, this does not pose a problem. In the text you find "where a is some unit vector", thus, the mathematician would formally write down . The space of possible values of is described by "It is a matter of indifference in the following whether denotes a single variable or a set, or even a set of functions, and whether the variables are discrete or continuous", which makes clear that the space of possible values of can arbitrary, but self-evident that it has to be fixed for a particular model.

Then, writing A(a,b,λ) = ±1 is a way a physicist writes down what a mathematician would write down as or more formal
.

[Joy Christian]

This is a physics paper, not a mathematical.

What a bunch of hypocritical nonsense.

One often hears that Bell has proven a "mathematical" "theorem." If so, then his mathematics is sloppy, and hence his "theorem" is no theorem at all, for the reasons I gave in my previous post.

On the other hand, if an excuse is found that his paper is after all a "physics" paper, then his physics is *incomplete*, because without the co-domain of his functions A and B being precisely S^3 and nothing else, the completeness criterion of EPR simply cannot be satisfied, and therefore Bell's "physics" argument is a non-starter.


In either case, Bell's so-called "theorem" is a piece of junk.

But I will leave this discussion now, for I have better things to do.

[Schmelzer]

One often hears that Bell has proven a "mathematical" "theorem." If so, then his mathematics is sloppy, and hence his "theorem" is no theorem at all, for the reasons I gave in my previous post.

His mathematics is not sloppy at all, the formal presentation of these mathematics follows the rules of physics journals, not of mathematical journals, that's all.

To translate them into the requirements of a more formal, mathematical journal is trivial, and I have given it:

On the other hand, if an excuse is found that his paper is after all a "physics" paper, then his physics is *incomplete*, because without the co-domain of his functions A and B being precisely S^3 and nothing else, the completeness criterion of EPR simply cannot be satisfied, and therefore Bell's "physics" argument is a non-starter.

The codomain is, clearly and obviously, . If you have some construction where , then it is irrelevant for Bell's theorem, except if you show that they reduce to . Because in this case the surrounding of by would be completely irrelevant, and you could, as well, use whatever embedding into whatever group G you like.

[Joy Christian]

In either case, Bell's so-called "theorem" is a piece of junk.

[minkwe]

Okay, it appears I went too fast but let us clarify a few things first. Please, Ilja and Joy, review paragraph 2 of Page 1 and answer this question for me please.

One sibling of a spin-1/2 pair (forget about the other sibling for a moment, let us focus on just one of them) leaves the source heading towards Alice. Alice picks a vector "a" to measure the particle. She has two regions of her Stern-Gerlach magnets labelled (+1, -1). The particle ends up in one of the two regions.

The expression:

A(a, λ) = ±1

Where λ represents everything else apart from "a" that is responsible for the outcome. This expression is simply a mathematical representation of the statements before it. I did not say λ was independent of activities happening at space-like separated distances. In fact I did not say λ could not be null, for example if such a complete specification is not possible. λ could be anything. So please, think about this again and tell me if you disagree. There is nothing in this expression that restricts it to local realistic theories. It applies to even QM!

Now the other sibling is heading toward Bob and we could write the exact same expression for it:
B(b, λ) = ±1

The third sentence of paragraph 2 on page one says that according to QM, for a pair of such particles

A(a, λ) = -B(a, λ) = ±1

Understood? Agreed?

[Joy Christian]

There is nothing in this expression that restricts it to local realistic theories. It applies to even QM!

Yes, I understand now. I know what you are getting at. But just to make sure let me put this in my words. What you are saying is that λ can be a function of either b, or B, or both, so that the result A(a, λ) at one station may be influenced by the activities at the remote station. Sure. In that case your sentence above is correct.

However, the function A(a, λ), by Bell's assumption of locality, does not depend on either b or B. This implicitly means that λ is not a function of either b or B.

[Schmelzer]

Okay, it appears I went too fast but let us clarify a few things first. Please, Ilja and Joy, review paragraph 2 of Page 1 and answer this question for me please.

One sibling of a spin-1/2 pair (forget about the other sibling for a moment, let us focus on just one of them) leaves the source heading towards Alice. Alice picks a vector "a" to measure the particle. She has two regions of her Stern-Gerlach magnets labelled (+1, -1). The particle ends up in one of the two regions.
The expression:
A(a, λ) = ±1
Where λ represents everything else apart from "a" that is responsible for the outcome. This expression is simply a mathematical representation of the statements before it.

I completely disagree. This would be an interpretation of the formula A(a, λ) = ±1 which takes it completely out of the context. In Bell's paper, this formula describes an intermediate result, after the application of the EPR argument to the physical situation.

The EPR argument gives the existence of λ, its independence of λ on a and be, and, given that the EPR criterion of reality is applied, also presumes a local realistic theory. Thus, the following claims have to be rejected:

I did not say λ was independent of activities happening at space-like separated distances. In fact I did not say λ could not be null, for example if such a complete specification is not possible. λ could be anything. So please, think about this again and tell me if you disagree. There is nothing in this expression that restricts it to local realistic theories.

I could accept to start discussion such a hypothesis - but this would require that you accept that, beginning with such a discussion, the whole consideration is about something completely different and has no relevance at all for Bell's theorem - comparable, say, to the relevance which a discussion about the esthetical value of putting on a Che T-shirt has for relativity.

The following requires a separate protest:

It applies to even QM!
The third sentence of paragraph 2 on page one says that according to QM, for a pair of such particles
A(a, λ) = -B(a, λ) = ±1

This means only that, if such functions exist, and the QM predictions are correct, then they have to fulfill these properties. But standard QM does not define them.

[Joy Christian]

Congratulations minkwe! I did not expect your trap to yield the desired outcome so quickly. Utter vacuity of Bell's assumptions is already becoming apparent.

[minkwe]

I completely disagree. This would be an interpretation of the formula A(a, λ) = ±1

This is not out of context as you claim. The point we are getting at is the question of whether there is anything in equation (1) that restricts λ from being non-local, other than what Bell might have had in his mind or what EPR may have had in mind. Ultimately what matters is what is encapsulated in the equations.

Do you agree that outcomes exist in QM?
Do you agree that for the situtation described by Bell in paragraph 2 on page one, the outcomes are ±1 by definition?
Do you agree that the measurement is along vectors chosen at the station?

If you agree to the above 3 statements, then please write down mathematically how you would express the fact that

1) A single particle leaving the source and interacting with magnet oriented along a vector "a" produces an outcome ±1?
2) For a pair of spin-1/2 particles heading in opposite directions but measured with magnets pointed along the same direction "a", according to QM, the outcome at one arm must be opposite to the outcome at the other arm.

Please could you write down those two expressions.

Here is my version of those two expressions
A(a, λ) = ±1
A(a, λ) = -B(a, λ) = ±1

You objected, so please what are yours. Note that there is no mention of any other vector other than "a", so don't be tempted to write A(a, b, λ) = ±1, like you did previously. Also, your other objections about lambda, apply just as well to something like A(a, b, λ) anyway so that line of argument gets you no where.

I could accept to start discussion such a hypothesis - but this would require that you accept that, beginning with such a discussion, the whole consideration is about something completely different

It is not completely different, we are aiming to unravel exactly what Bell, and probably you think equation (1) in Bell's paper is representing. I aim to show that it does not represent what both of you and many others think it does, as you will find out when you try to write down the requested expressions above. After that we will proceed to show that even equation (2) does not represent what Bell or you think it does.

Evidently, you believe equation (1) encapsulates locality. But equation (1) will not be different if λ were non-local? So I await your two expressions.

This means only that, if such functions exist, and the QM predictions are correct, then they have to fulfill these properties. But standard QM does not define them.

Are you claiming that outcomes and settings do not exist in QM? If not, please show us the equation which encapsulates the fact that a single particle measured at along a given axis, produces outcomes ±1, and two such spin-1/2 particles heading in opposite directions measured along the same vector "a" produce opposite outcomes?

[minkwe]

Congratulations minkwe! I did not expect your trap to yield the desired outcome so quickly. Utter vacuity of Bell's assumptions is already becoming apparent.

Thanks, but I don't want to trap anyone, so I always allow for people to change their minds and retract previous agreements or disagreements. So even if Ilya accepts my arguments now, I allow for him to later retract his agreements. Progress is what we are all after.

[Schmelzer]

The point we are getting at is the question of whether there is anything in equation (1) that restricts λ from being non-local, other than what Bell might have had in his mind or what EPR may have had in mind. Ultimately what matters is what is encapsulated in the equations.

Do you agree that outcomes exist in QM?

Outcomes exist in reality, but are not defined by QM. QM defines only probabilities for the outcomes.

Do you agree that for the situtation described by Bell in paragraph 2 on page one, the outcomes are ±1 by definition?
Do you agree that the measurement is along vectors chosen at the station?

Yes and yes.

If you agree to the above 3 statements, then please write down mathematically how you would express the fact that
1) A single particle leaving the source and interacting with magnet oriented along a vector "a" produces an outcome ±1?
2) For a pair of spin-1/2 particles heading in opposite directions but measured with magnets pointed along the same direction "a", according to QM, the outcome at one arm must be opposite to the outcome at the other arm.

I would not write them down mathematically, because I see no reason for this. But, ok, I could write . But in such a case I would prefer the verbal description.

It is not completely different, we are aiming to unravel exactly what Bell, and probably you think equation (1) in Bell's paper is representing. I aim to show that it does not represent what both of you and many others think it does, as you will find out when you try to write down the requested expressions above. After that we will proceed to show that even equation (2) does not represent what Bell or you think it does.

I do not understand how the request to write down something completely different in a mathematical form will reach this, but, so what, let's see.

Evidently, you believe equation (1) encapsulates locality. But equation (1) will not be different if λ were non-local? So I await your two expressions.

I do not think that the expression (1) somehow by symbol magic enforces locality. I think that the context - the EPR argument used to describe what is the λ - is what requires that (1) is local. You may be free to use the formula A(a,λ)=±1 on your T-shirt because of its esthetic value, and give it the meaning that λ denotes the Nirvana and ±1 Yin and Yan, but this would not be the context of Bell's inequality.

Are you claiming that outcomes and settings do not exist in QM?

No, I claim that QM does not have any formulas to compute the outcomes, except in some particular cases (repeated measurements of eigenstates).

[Schmelzer]

A question I think about is the appropriate techniques of behaviour, if one argues, as a defender of a minority opinion, against a proponent of the majority opinion.

I have always assumed that the only chance for a minority opinion is to have the better arguments. So, one should always show that one has the better arguments. To use aggressive attacks like

What a bunch of hypocritical nonsense.

would be, in this case, completely counterproductive, simply because there is a wide agreement that starting personal attacks is typical for those who have lost the argumentative battle, who have no more arguments about the content, or only very weak ones, and knows about this. In a similar way,

But I will leave this discussion now, for I have better things to do.

is usually interpreted as an attempt to hide that one leaves a discussion because one does not have reasonable arguments.

And statements like

Congratulations minkwe! I did not expect your trap to yield the desired outcome so quickly.

are usually interpreted as showing something about the author himself - that he likes entrapment and uses it himself.

But these are, of course, only my personal impressions about how mainstream scientists would react. I have never thought about alternative strategies, based on the creation of a small group of "true believers", which could be a base for developing a revolution. Correspondingly, I have no "true believer" into my ether theories. The techniques to collect such "true believers" could be, in fact, very different from those which I consider as reasonable in a scientific discussion.



But these are, of course, only my personal impressions about how mainstream scientists would react. I have never thought about alternative strategies, based on the creation of a small group of "true believers", which could be a base for developing a revolution. Correspondingly, I have no "true believer" into my ether theories. The techniques to collect such "true believers" could be, in fact, very different from those which I consider as reasonable in a scientific discussion.

[Joy Christian]

And what about this one?

In either case, Bell's so-called "theorem" is a piece of junk.

And this one?

Utter vacuity of Bell's assumptions is already becoming apparent.

[Heinera]

You meant

[Schmelzer]

You meant

Thanks