Coming Soon!

[FrediFizzx]

@gill1109 Well, thank you for your praise but we didn't need all the excess nonsense to go with it. It is for sure a Gill killer. No doubt about it.
.

[gill1109]

@gill1109 Well, thank you for your praise but we didn't need all the excess nonsense to go with it. It is for sure a Gill killer. No doubt about it.

I'm still very much alive. Good luck with getting this published...

Everyone can read your code and come to their own conclusions.

[FrediFizzx]

@gill1109 No problem. I just took the zeroes out. What say you now?

https://www.wolframcloud.com/obj/fredif ... v-simp2.nb



EPRsims/newCS-23-2hv-simp2.pdf
EPRsims/newCS-23-2hv-simp2.nb

Enjoy the 100 percent local Gill theory killer!
.

[gill1109]

And now in R, CHSH:

Code: Select all

set.seed(1234)
M <- 1000000
theta <- runif(M, 0, 360)
beta1 <- 0.32
beta2 <- 0.938
phi <- 3
xi <- 0
s1 <- theta
s2 <- theta + 180
cosD <- function(x) cos(pi * x / 180)
sinD <- function(x) sin(pi * x / 180)
lambda1 <- beta1 * cos(theta/phi)^2
lambda2 <- beta2 * cos(theta/phi)^2

a <- 0
b <- 45
Aa1 <- ifelse(abs(cosD(a - s1)) > lambda1, sign(cosD(a - s1)), 0)
Aa2 <- ifelse(abs(cosD(a - s1)) < lambda2, sign(sinD(a - s1 + xi)), 0)
Bb1 <- ifelse(abs(cosD(b - s2)) > lambda1, sign(cosD(b - s2)), 0)
Bb2 <- ifelse(abs(cosD(b - s2)) < lambda2, sign(sinD(b - s2 + xi)), 0)
sum(Aa1*Bb1 + Aa2*Bb2)/(sum(Aa1*Bb1 != 0) + (sum(Aa2*Bb2 != 0)))

a <- 0
b <- 135
Aa1 <- ifelse(abs(cosD(a - s1)) > lambda1, sign(cosD(a - s1)), 0)
Aa2 <- ifelse(abs(cosD(a - s1)) < lambda2, sign(sinD(a - s1 + xi)), 0)
Bb1 <- ifelse(abs(cosD(b - s2)) > lambda1, sign(cosD(b - s2)), 0)
Bb2 <- ifelse(abs(cosD(b - s2)) < lambda2, sign(sinD(b - s2 + xi)), 0)
sum(Aa1*Bb1 + Aa2*Bb2)/(sum(Aa1*Bb1 != 0) + (sum(Aa2*Bb2 != 0)))

a <- 90
b <- 45
Aa1 <- ifelse(abs(cosD(a - s1)) > lambda1, sign(cosD(a - s1)), 0)
Aa2 <- ifelse(abs(cosD(a - s1)) < lambda2, sign(sinD(a - s1 + xi)), 0)
Bb1 <- ifelse(abs(cosD(b - s2)) > lambda1, sign(cosD(b - s2)), 0)
Bb2 <- ifelse(abs(cosD(b - s2)) < lambda2, sign(sinD(b - s2 + xi)), 0)
sum(Aa1*Bb1 + Aa2*Bb2)/(sum(Aa1*Bb1 != 0) + (sum(Aa2*Bb2 != 0)))

a <- 90
b <- 135
Aa1 <- ifelse(abs(cosD(a - s1)) > lambda1, sign(cosD(a - s1)), 0)
Aa2 <- ifelse(abs(cosD(a - s1)) < lambda2, sign(sinD(a - s1 + xi)), 0)
Bb1 <- ifelse(abs(cosD(b - s2)) > lambda1, sign(cosD(b - s2)), 0)
Bb2 <- ifelse(abs(cosD(b - s2)) < lambda2, sign(sinD(b - s2 + xi)), 0)
sum(Aa1*Bb1 + Aa2*Bb2)/(sum(Aa1*Bb1 != 0) + (sum(Aa2*Bb2 != 0)))

The four correlations are: -0.706443, +0.690584, -0.6907836, -0.6815394

S = 2.76935

2 * sqrt(2) = 2.828427

Indeed, 100%. local!

On a second run: -0.7064589, +0.6889165, -0.6910514, -0.6810689
S = 2.767496

That gives you an idea of the statistical errors with a sample size of 1 million.

[FrediFizzx]

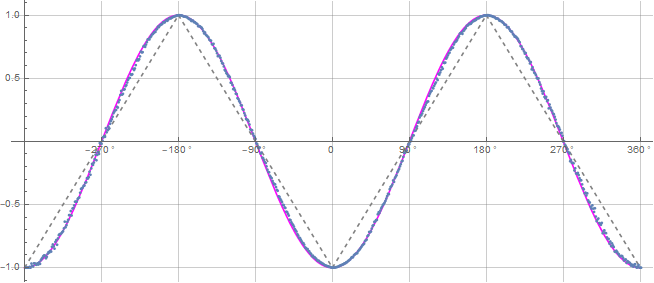
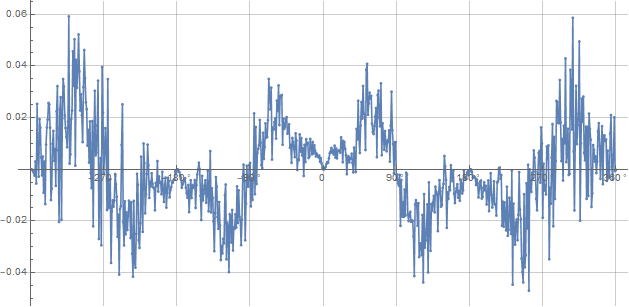
@gill1109 LOL! Pretty easy to see that from the 5 million event plot. You're finished. Time to get real, get over it and move on!

Deviation from the -cosine curve.


.

[gill1109]

Here's a variation on Fred's code. I've added a fair coin toss on each trial which determines both for Alice and for Bob whether they use detector 1 or detector 2. This is closer to Joy's models with something like a spinorial spin-flip.

Code: Select all

set.seed(1234)
M <- 10000
theta <- runif(M, 0, 360)
beta1 <- 0.32
beta2 <- 0.938
phi <- 3
xi <- 0
s1 <- theta
s2 <- theta + 180
cosD <- function(x) cos(pi * x / 180)
sinD <- function(x) sin(pi * x / 180)
lambda1 <- beta1 * cos(theta/phi)^2
lambda2 <- beta2 * cos(theta/phi)^2
coins <- sample(c("H", "T"), M, replace = TRUE)

a <- 0
b <- 45
Aa1 <- ifelse(abs(cosD(a - s1)) > lambda1, sign(cosD(a - s1)), 0)
Aa2 <- ifelse(abs(cosD(a - s1)) < lambda2, sign(sinD(a - s1 + xi)), 0)
A <- ifelse(coins =="H", Aa1, Aa2)
Bb1 <- ifelse(abs(cosD(b - s2)) > lambda1, sign(cosD(b - s2)), 0)
Bb2 <- ifelse(abs(cosD(b - s2)) < lambda2, sign(sinD(b - s2 + xi)), 0)
B <- ifelse(coins =="H", Bb1, Bb2)
sum(A*B)/sum(A*B != 0)


a <- 0
b <- 135
Aa1 <- ifelse(abs(cosD(a - s1)) > lambda1, sign(cosD(a - s1)), 0)
Aa2 <- ifelse(abs(cosD(a - s1)) < lambda2, sign(sinD(a - s1 + xi)), 0)
A <- ifelse(coins =="H", Aa1, Aa2)
Bb1 <- ifelse(abs(cosD(b - s2)) > lambda1, sign(cosD(b - s2)), 0)
Bb2 <- ifelse(abs(cosD(b - s2)) < lambda2, sign(sinD(b - s2 + xi)), 0)
B <- ifelse(coins =="H", Bb1, Bb2)
sum(A*B)/sum(A*B != 0)

a <- 90
b <- 45
Aa1 <- ifelse(abs(cosD(a - s1)) > lambda1, sign(cosD(a - s1)), 0)
Aa2 <- ifelse(abs(cosD(a - s1)) < lambda2, sign(sinD(a - s1 + xi)), 0)
A <- ifelse(coins =="H", Aa1, Aa2)
Bb1 <- ifelse(abs(cosD(b - s2)) > lambda1, sign(cosD(b - s2)), 0)
Bb2 <- ifelse(abs(cosD(b - s2)) < lambda2, sign(sinD(b - s2 + xi)), 0)
B <- ifelse(coins =="H", Bb1, Bb2)
sum(A*B)/sum(A*B != 0)

a <- 90
b <- 135
Aa1 <- ifelse(abs(cosD(a - s1)) > lambda1, sign(cosD(a - s1)), 0)
Aa2 <- ifelse(abs(cosD(a - s1)) < lambda2, sign(sinD(a - s1 + xi)), 0)
A <- ifelse(coins =="H", Aa1, Aa2)
Bb1 <- ifelse(abs(cosD(b - s2)) > lambda1, sign(cosD(b - s2)), 0)
Bb2 <- ifelse(abs(cosD(b - s2)) < lambda2, sign(sinD(b - s2 + xi)), 0)
B <- ifelse(coins =="H", Bb1, Bb2)
sum(A*B)/sum(A*B != 0)


However, it is in fact a detection loophole model, with detection rate of about 50% per trial.

Code: Select all

> sum(A*B == 0)/M
[1] 0.5079
>

[jreed]

@gill1109 No problem. I just took the zeroes out. What say you now?

https://www.wolframcloud.com/obj/fredif ... v-simp2.nb



EPRsims/newCS-23-2hv-simp2.pdf
EPRsims/newCS-23-2hv-simp2.nb

Enjoy the 100 percent local Gill theory killer!
.

Great work Fred. You got rid of all that magic code, and still obtained a perfect cosine. Now we are back to the old detection loophole again. I ran the code with 10,000 trials and found that your routine actually generated 20,000 trials from the two tests using lambda1 and lambda2. In the A channel, 12,393 are detected trials, and the rest, 7607, are "no result" trials. In the B channel, 12,439 are good and 7561 are "no result". When the results are analyzed, these "no result" trials are dropped. That's the detection loophole. You must have spent some time fine tuning this to get the near perfect cosine. I'm impressed.

[gill1109]

@gill1109 No problem. I just took the zeroes out. What say you now?

https://www.wolframcloud.com/obj/fredif ... v-simp2.nb



EPRsims/newCS-23-2hv-simp2.pdf
EPRsims/newCS-23-2hv-simp2.nb

Enjoy the 100 percent local Gill theory killer!
.

Great work Fred. You got rid of all that magic code, and still obtained a perfect cosine. Now we are back to the old detection loophole again. I ran the code with 10,000 trials and found that your routine actually generated 20,000 trials from the two tests using lambda1 and lambda2. In the A channel, 12,393 are detected trials, and the rest, 7607, are "no result" trials. In the B channel, 12,439 are good and 7561 are "no result". When the results are analyzed, these "no result" trials are dropped. That's the detection loophole. You must have spent some time fine tuning this to get the near perfect cosine. I'm impressed.

Yes John it’s the good old detection loophole but with two sets of measurement outcomes per trial. Channel 1 and Channel 2. I added a further coin toss (a spinorial quaternionic spin flip?) to choose just one set, channel 1 or channel 2, both for Alice and Bob. All 100% local. Overal efficiency: 50%.

[FrediFizzx]

@jreed Sorry, there is no detection loophole. 5 million trials, Total Events=4,992,002. Oops, lost a few in the analysis. Not enough for detection loophole. Lucky for us, the analysis process takes out all those "no result" artifacts. You Bell fanatics are finished!
.

[Joy Christian]

@jreed Sorry, there is no detection loophole. 5 million trials, Total Events=4,992,002. Oops, lost a few in the analysis. Not enough for detection loophole. Lucky for us, the analysis process takes out all those "no result" artifacts. You Bell fanatics are finished!

About 0.16% of events are missing. Where did they go?
.

[FrediFizzx]

@jreed Sorry, there is no detection loophole. 5 million trials, Total Events=4,992,002. Oops, lost a few in the analysis. Not enough for detection loophole. Lucky for us, the analysis process takes out all those "no result" artifacts. You Bell fanatics are finished!

About 0.16% of events are missing. Where did they go?

Well, that is not very many, less than 1 percent. Definitely not enough for any detection loophole! Must have got chewed up with the artifacts. But I can probably dial that in. We will give it a shot.
.

[FrediFizzx]

I can't believe you Bell fanatics can't figure this simulation out. It is so easy.
.

[jreed]

I can't believe you Bell fanatics can't figure this simulation out. It is so easy.
.

Here's a little question for you:
In your program add the following statement: Total[Abs[A]] after the statement A=outA[[All,2]];. Then rerun the program with however many trials you want.
What do you think the resulting output of Total means? You can do the same for the B part by adding Total[Abs[B]].

[FrediFizzx]

I can't believe you Bell fanatics can't figure this simulation out. It is so easy.
.

Here's a little question for you:
In your program add the following statement: Total[Abs[A]] after the statement A=outA[[All,2]];. Then rerun the program with however many trials you want.
What do you think the resulting output of Total means? You can do the same for the B part by adding Total[Abs[B]].

I don't have to even do that as I know what the result will be. Half of the suckers are artifacts. We know the "no results" are artifacts then the rest of the other over whatever m is are artifacts matching the other side. So the analysis process weeds them all out. It's perfect.
.

[gill1109]

I can't believe you Bell fanatics can't figure this simulation out. It is so easy.
.

Here's a little question for you:
In your program add the following statement: Total[Abs[A]] after the statement A=outA[[All,2]];. Then rerun the program with however many trials you want.
What do you think the resulting output of Total means? You can do the same for the B part by adding Total[Abs[B]].

I don't have to even do that as I know what the result will be. Half of the suckers are artifacts. We know the "no results" are artifacts then the rest of the other over whatever m is are artifacts matching the other side. So the analysis process weeds them all out. It's perfect.
.

Yes it’s perfect, I already said it’s quite brilliant.

You call them artefacts. I call them “no shows”.

Write one set of comments in the code and come up with some suggestive names of key variables, and it’s an amusing simulation of an original but inefficient (low detector efficiency) detection loophole experiment. Ternary outcomes: -1, 0, +1. Spin down, no detection, spin up. As you should know, photons are actually spin 1 particles, not spin 1/2.

Write a different set of comments and use other suggestive names of key variables, and it’s a brilliant simulation of the physics in Joy’s epoch-making 2007 disproof of Bell’s theorem paper as later extended in his IEEE Access and RSOS papers.

I already showed you R code where I used an extra quaternionic coin-flip (a Bertlmann’s sock, if you like) to make half of the artefacts disappear in a more elegant way and link the simulation more closely to Joy’s works.

[FrediFizzx]

@gill1109 Nope! You have it all wrong. Besides the "no results" there are other artifacts that the analysis process takes out. There is absolutely no detection loophole happening here since I get almost the same number of events after analysis processing as the trial numbers we started with. And I get the same angles a and b out as went in. So, no conspiracy is happening either.
.

[gill1109]

@gill1109 Nope! You have it all wrong. Besides the "no results" there are other artifacts that the analysis process takes out. There is absolutely no detection loophole happening here since I get almost the same number of events after analysis processing as the trial numbers we started with. And I get the same angles a and b out as went in. So, no conspiracy is happening either.

First you double the number of outcome sets by using two channels at once, and later you delete half again!

Very clever!

The code is crystal clear. Congratulations. Nice work.

But there are also measurement outcomes equal to zero. You may call them artefacts if you like, but these are taken out too. If you plot the number of complete data points as function of the difference between the two measurement angles you will probably see the same defect as Pearle already noticed in his model. Detection rate on each side, given setting, depends on the angle on the other side!
https://arxiv.org/abs/1505.04431
Pearle's Hidden-Variable Model Revisited
Richard D. Gill
Pearle (1970) gave an example of a local hidden variables model which exactly reproduced the singlet correlations of quantum theory, through the device of data-rejection: particles can fail to be detected in a way which depends on the hidden variables carried by the particles and on the measurement settings. If the experimenter computes correlations between measurement outcomes of particle pairs for which both particles are detected, he is actually looking at a subsample of particle pairs, determined by interaction involving both measurement settings and the hidden variables carried in the particles. We correct a mistake in Pearle's formulas (a normalization error) and more importantly show that the model is more simple than first appears. We illustrate with visualisations of the model and with a small simulation experiment, with code in the statistical programming language R included in the paper. Open problems are discussed.
Entropy 2020, 22(1), 1; https://doi.org/10.3390/e22010001
DOI: 10.3390/e22010001

@gill1109 Nope! You have it all wrong. Besides the "no results" there are other artifacts that the analysis process takes out. There is absolutely no detection loophole happening here since I get almost the same number of events after analysis processing as the trial numbers we started with. And I get the same angles a and b out as went in. So, no conspiracy is happening either.

First you double the number of outcome sets by using two channels at once, and later you delete half again!

I don't delete the other half of junk artifacts, the analysis process does it automatically. It is where the A and B matching belongs. If it don't match, it is gone.

Yes it is done automatically by the code which you wrote. I already said it was very clear and very clever. It is what it is.

[FrediFizzx]

@gill1109 Nope! You have it all wrong. Besides the "no results" there are other artifacts that the analysis process takes out. There is absolutely no detection loophole happening here since I get almost the same number of events after analysis processing as the trial numbers we started with. And I get the same angles a and b out as went in. So, no conspiracy is happening either.

First you double the number of outcome sets by using two channels at once, and later you delete half again!

I don't delete the other half of junk artifacts, the analysis process does it automatically. It is where the A and B matching belongs. If it don't match, it is gone.
.

[gill1109]

@gill1109 Nope! You have it all wrong. Besides the "no results" there are other artifacts that the analysis process takes out. There is absolutely no detection loophole happening here since I get almost the same number of events after analysis processing as the trial numbers we started with. And I get the same angles a and b out as went in. So, no conspiracy is happening either.

First you double the number of outcome sets by using two channels at once, and later you delete half again!

I don't delete the other half of junk artifacts, the analysis process does it automatically. It is where the A and B matching belongs. If it don't match, it is gone.

You wrote the analysis process. It removes about half the data, twice. The first half because you introduced two channels: each trial results in two pairs of outcomes, but usually one of them includes a zero outcome. The second half, again, because you allowed outcomes to equal “0” as well as +/-1. When you compute correlations, you divide the sum of products of the outcomes by the number of products unequal to 0.

You can say that no data was thrown away, but you must admit, I hope, that you finally get the same results *as if* all data with one of the outcomes zero, is thrown away.

Take a look at my alternative R code where I use a Bertlmann’s socks coin toss to decide, for each trial separately, whether to keep channel 1 or channel 2. Later I’ll investigate whether your model has the same defects as Pearle’s, and as other similar models (Michel’s; Caroline Thompson’s: …). Read my paper about the Pearle model for further information.

My alternative code results in a model closer to Joy’s, with an extra hidden variable being a fair coin toss. It should interest you both.

[FrediFizzx]

@gill1109 Nothing can be thrown away until the analysis section does it. I didn't write the analysis section. John did a very long time ago from what Michel did in Python.
.