minkwe wrote:But let me Press you some more there, for a single particle heading toward a station oriented along vector "a", what exactly do your terms A, B, AB, mean?
For a single particle A would mean the measurement result, which is in
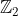
, and B together with AB would not have a meaning, because this would presuppose the other particle.
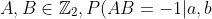=1 if a=b)
minkwe wrote:Is too imprecise. It does not identify the outcomes with the magnet directions. I seek two expressions:
1) should represent the fact, stated in the definition of the problem, that the outcomes are ±1 for a single particle measured along "a"
2) the second should represent the fact that, for two such entangled spin-1/2 particles, measured along the same axis "a", the outcomes are opposite.
I cannot follow. (1) is clearly represented by

. And (2) by
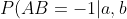=1 if a=b)
minkwe wrote:Do you have any problem with these:?


That is, do you disagree that these expressions are universally true, even for QM.
I actually see no problem for QM. I have a general philosophical problem with statements being "universally true", independent of a particular theory.
minkwe wrote:Those two facts are the premises of the paper, and are universally true even for QM, and involve no ambiguity that should require a treatment using probabilities. Can you agree to that?
No. The connection between A and a is, of course ambigious and requires a treatment using probabilities.

suggests some functional dependence for which there is no base in QM.
minkwe wrote:Do you understand the difference between:
* If λ is local, then A(a,λ) = +/-1
* If A(a,λ) = +/-1, then λ is local
If so, then you should also understand exactly why it is important to distinguish between necessary and sufficient conditions in mathematical arguments. It ultimately determines how logically sound our arguments are.
Oh, sorry, I'm completely stupid, never heard about such a thing like a difference between necessary and sufficient conditions, can you explain? Or what do you want to hear?
minkwe wrote:I asked you for an expression representing mathematically the basic facts of the experiment as described by Bell himself, in a manner which applies just as well to QM as to local theories.
And why do you think I should find such an animal?
minkwe wrote:Do you agree that equation (1) would be exactly the same even if λ represented non-local hidden variables? Even if we all agree that when Bell wrote equation (1) he was thinking about local hidden variables.
The question is incorrect, because "local hidden variables" as well as "non-local hidden variables" is simply sloppy language. If I have accepted that sloppy language in earlier answers, I should remove this as inaccurate. What is local or nonlocal is the realistic theory.
Locality is used (and necessary) for the EPR argument, and gives two results:
1.) The values A, B are predefined, thus, there exists some hidden variables so that A=A(a,b,λ) and B=B(a,b,λ).
2.) These λ have a probability distribution which cannot depend on a,b, because λ is predefined, that means, defined before a, b come into existence.
3.) A should not depend on b and B not on a.
minkwe wrote:Second point I want to raise is that if you agree with my previous answer to my own question, that we could represent the facts of the experiment described in the second paragraph on page 1 with

,
where

represents the outcome of a single particle at Alice's station, when measured along direction "a", and

represents the outcome of a single particle at Alice's station, when measured along direction "b".
then we could also introduce λ in this expression to give
 = -B_a(\lambda) = \pm1)
,
If you introduce it, you would have to describe what they mean. And, whatever you use at this description, it is highly probable that, then, the two equations mean something very different than the equations in Bell's paper, where the λ is defined using the EPR argument, which leads to some properties of λ which are important.
Note: Mathematics is only language, a little bit more formalized than everyday language, but this does not change the fact that formulas have a meaning only in a context.
minkwe wrote:And hopefully, you don't have any problem with this expression either. Now obviously Bell was thinking about λ as being local hidden variables, but hopefully you also agree that the expression will be exactly the same if λ represented non-local hidden variables. If all of this is acceptable to you, we can proceed to equation (2).
I have the problem that you have completely changed the context, thus, the object λ derived from the EPR argument (which has properties which follow from the derivation) is replaced by some abstract λ without any properties. That means, the context is modified, and therefore the formula obtains a different meaning. If you interpret, for example, λ as "everything which is somehow responsible for the output A, B", and don't have the context of the EPR argument, you could, for example, now write formula (2) with
 d\lambda)
or some other manipulation.
. But in such a case I would prefer the verbal description.

