Yablon wrote:In the process of doing this development, it occurred to me that certain solutions of the Dirac monopole had never been fully developed, and as I explored those states which had been "left on the table" by others, I began to realize that this could be used to account fully and completely for the fractionalized charge pattern observed in the Fractional Quantum Hall Effect. So over the weekend I wrote up an 11 page paper you may review at
http://vixra.org/pdf/1411.0552v1.pdf, which as of Thursday I had no anticipation of writing. I do not think of myself as a condensed matter theorist, so I felt a bit like a fish out of water, but managed to do enough review of this area and got some private comments from a friend who is a professional condensed matter theorist, all of which made me comfortable I was not too badly off any bases. I also submitted this paper to PRD, and will let you know what happens.
I promised to share whatever happens, so let me do so. Erick Weinberg, the PRD Chief Editor, rejected this paper last week without review, saying that:
E. Weinberg / PRD wrote:This falls outside the scope of Physical Review D, and should instead be directed to a condensed matter journal.
I did not agree, and resubmitted with the following arguments:
Yablon wrote:I must respectfully record my disagreement with your dismissing my manuscript from consideration that DY11422 on the basis that it “falls outside the scope of Physical Review D, and should instead be directed to a condensed matter journal.”
At the link
https://journals.aps.org/prd/about it is stated that “D15: covers general relativity, quantum theory of gravitation, cosmology, particle astrophysics, formal aspects of theory of particles and fields, general and formal development in gauge field theories and string theory.” This paper – if it is correct which you have not yet opined about – is most definitively an important “development in gauge field theories and string theory” which fits squarely within the scope of PRD.
The relationship which this paper bears to condensed matter rests in the fact that it demonstrates the power of gauge theory to explain a condensed matter phenomenon – namely the observed fractionalization of electric charge as observed under certain circumstances – strictly on the basis of formal gauge theory without resort to the condensed matter methodologies which are usually thought to be required for explanation.
Ever since Hermann Weyl developed gauge theory from 1918 to 1929 as an invariance under certain changes in phase with geometric roots in the curvature i.e. electromagnetic field of a gauge space, some of the most important theoretical advances in physics have been findings which extend the reach of gauge theories and demonstrate their power to explain a very broad range of observational data. Yang and Mills in 1954 extended the capacity of gauge theories by laying the foundation for these theories to eventually explain strong and weak interactions as factors in the phenomenological group SU(3)_C x S(2)_W x U(1)_Y. Weinberg and Salam, aided by developments in how to use the degrees of freedom in scalar fields to spontaneously break symmetry, explained the electroweak interaction on the basis of breaking S(2)_W x U(1)_Y down to the observed U(1)_em. Georgi and Glashow showed how SU(3)_C x S(2)_W x U(1)_Y could itself be obtained by breaking the symmetry of a larger simple group G which contains all of the strong, weak and electromagnetic interactions and the particles whose interactions they mediate, and used SU(5) as a demonstration of how this approach might work. Each of these developments were important because they showed how gauge theory could be extended to explain phenomenology well beyond what was known by Weyl and others back in 1929.
The specific focus of this paper, is to demonstrate that gauge theory is also powerful enough to be extended into the purview of phenomenon for which are thought to require a condensed matter explanation but which I show actually are grounded in gauge theory, and indeed, in the U(1)_em gauge theory of electromagnetism. The genealogical lineage of this approach starts with Dirac’s showing in 1931 that if one postulates a magnetic charge and uses a Dirac string connected from that charge to spatial infinity, then the electric charge must be quantized. (And I note that string theory is also within the scope of PRD.) In the mid-1970s Wu and Yang showed that the exact same result could be obtained without strings, using the indeterminacy at the north and south poles of an azimuth over a closed two-dimensional surface S^2 embedded in the three-dimensional space of physical experience. In Dirac’s original conception the gauge potential is defined everywhere except along the string over which it is indeterminate; Wu and Yang placed situated this indeterminacy at the north and south poles of S^2 and then absorbed this into a gauge transformation yielding the exact charge quantization that Dirac had found. What I demonstrate in this manuscript is that not only does this approach predict charge quantization, but it also predicts charge fractionalization. That is: gauge theory, when logically extended along the path laid out by Wu and Yang, predicts charge quantization and charge fractionalization.
It is certainly notable that the predicted fractionalization is observed in condensed matter environments of low temperature when magnetic fields are applied to certain materials. But what is notable is not that fractionalization is a condensed matter phenomenon, but that this condensed matter phenomenon is a logical consequence of gauge theory as applied by Wu and Yang, upon additional consideration of spinor orientation / entanglement relationships. Any advance which notably extends the reach of gauge theory beyond present understandings is within the scope of PRD. By demonstrating the power of gauge theory to be extended even further beyond its presently-known reach into a phenomenon presently thought to require a separate and distinct condensed matter explanation, this manuscript is most certainly within the scope of PRD.
Accordingly, I respectfully request reconsideration of your decision, and ask you to please review this work on its merits with view toward publication in PRD if it is found to be substantively sound.
I did not expect this to be accepted at PRD, but my goal in pressing was to force a substantive review, not just bureaucratic jousting over which journal covers what turf. Just this evening, I received another rejection, this time with the following review that is more substantive, and in my view, wrong:
E. Weinberg / PRD wrote:I find your arguments that this paper falls within the scope of Physical Review D unpersuasive. It is true that the scope of PRD is described as including gauge and string theories. However, the only gauge theory involved here is electromagnetism, and there was certainly no intention to claim that all papers involving electromagnetism should go to PRD rather than to PRA, PRB, or PRE. It is also true that the line of gauge singularities running from the monopole to infinity is often called a Dirac string, but that "string" has absolutely nothing to do with string theory.
In any case, the issue is really moot, because the paper is wrong:
1) If a monopole exists, then all particles carrying only electromagnetic charge must obey obey Eq. (1.7). They will therefore also trivially obey the weaker conditions of Eq. (2.2). However, the converse is certainly not true: obeying (2.2) but not (1.7) is not allowed. These statements have nothing to do with the spin of the particle.
2) Applying the Dirac-Wu-Yang arguments to the fractionally charged quasiparticles in FQHE systems is nontrivial. At the most fundamental level there is no issue. These systems are composed of electrons, protons, and neutrons, and there are no fractionally charged particles. At the level of analysis where the quasiparticle language applies, the system is fundamentally a two-dimensional one, whereas the Dirac-Wu-Yang argument is depends essentially on three-dimensional geometry.
The jurisdictional stuff is just chatter, let's get to the rejection points 1 and 2.
As to point 1, let me write down my equations (1.7) and (2.2):
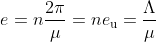
, (1.7)
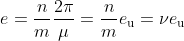
, (2.2)
where (2.2) goes together with the "filling factor''

. (2.3)
I agree with E. Weinberg that "If a monopole exists, then all particles carrying only electromagnetic charge must obey obey Eq. (1.7)." I also agree that "They will therefore also obey the conditions of Eq. (2.2)," but the words "trivially" and "weaker" are gratuitous. It is important to understand that the DCQ predicts charge fractionalization. As far as I know nobody has noticed this before, and that is not "trivial." Perhaps the (2.2) conditions are "weaker" in that they permit more charge states than does the quantized
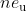
, but if those fractionalized charge states happen to be observed anywhere in the physical world under any set of circumstance however limited, then whether you call them weaker or call them Frisbees, they are important to understand. I also agree with E. Weinberg that "the converse is certainly not true: obeying (2.2) but not (1.7) is not allowed."
I have not said it is allowed. The m=1 state in my (2.2), see (2.3), is precisely (1.7). (2.2) includes (1.7) as its m=1 subset.
If I am missing something that Weinberg is trying to say, please help me out. The final statement that "These statements have nothing to do with the spin of the particle" goes to the heart of how we interpret these results, and
that leads to point 2.
Point 2 goes to the heart of the matter, and it was this sort of review I wanted to extract from E. Weinberg because it helps me understand what I need to explain to potential readers. I totally agree that "Applying the Dirac-Wu-Yang arguments to the fractionally charged quasiparticles in FQHE systems is nontrivial." I read his statement that "At the most fundamental level there is no issue" to really be saying that at the most fundamental level there is
no connection. If that is so, then that is precisely what I am trying to contradict with this paper.
I believe there is a connection. I agree that when Dirac uses strings to predict the DQC or the Dirac monopoles, or when Wu and Yang do the same thing without strings, they are working with "systems ... composed of electrons, protons, and neutrons, and there are no fractionally charged particles."
But we also know that under certain circumstances, at ultra-low temperatures, and inside of certain materials, as Weinberg correctly states, "the system is fundamentally a two-dimensional one, whereas the Dirac-Wu-Yang argument is depends essentially on three-dimensional geometry." This is, indeed, "at the level of analysis where the quasiparticle language applies." Weinberg's conclusion is that because of this, there is no connection, i.e., no "issue." My contrary conclusion is that there is a real connection, and that connection needs to be understood.
My paper spells out the role of orientation / entanglement in this connection, so I will not repeat that here in any detail. But think about what is physically happening when you take a Dirac-Wu-Yang gauge theory problem in three space dimensions, turn the temperature way down so as to "clamp down" on the electrons, and force them into a two dimensional system where the material employed has removed a spatial degree of freedom. In that that two dimensional, ultra-cold system, the environment of the electrons is bearing down on them in a way that does not ordinarily occur in warmer three-dimensional systems. Misner, Throne and Wheeler teach that electrons
are entangled with their environment, even in three dimensions. But there is clearly something about the low temperature and the two-dimensional restriction which causes the entanglement to manifest itself in what is physically observed. One might envision that in three dimensions and at higher temperatures, whatever "entanglement" an electron might find itself in is easily straightened out and so not readily observed in physical, observable manifestation. But when you cool down enough and take away a degree of freedom, you have "cornered" or "trapped" the electron and now it finds itself in states where its entanglement relationships are physically observed via FQHE with the filling factors
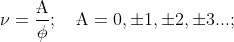
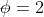
--or--

(3.2).
That also means, as I state at the end of my section 3, that "to the degree that the filling factors (3.2) do describe a feature of the natural world but only under these specialized conditions, and because (3.3) [for

] is integrally related to (3.2), it would appear that the non-zero magnetic fluxes

of Dirac monopoles (as distinguished from other types of monopole)
would only evidence themselves in nature under equally-restricted conditions."
Let me put this a bit differently. The Dirac-Wu-Yang arguments do predict that if magnetic monopoles exist, then both electric and magnetic charges are quantized, and as I have shown, they also predict charge fractionalization, and if we only count the states that differ by a
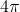
azimuth, these will have odd-denominators-only. Now, in the three-dimensional space of Dirac-Wu-Yang arguments none of these is
observed with the exception of charge quantization for electric charges only. There are no magnetic monopoles, there is no fractionalization, and the modern-day understanding of charge quantization is
not based on the DQC, but is based on the Yang-Mills generator Q=Y/2+I^3 which arises from spontaneous symmetry breaking. So: Dirac-Wu-Yang is elegant and beautiful but wrong (i.e., not physically observed), except at "the level of analysis where the quasiparticle language applies [and] the system is fundamentally a two-dimensional one." There, and only there, nature puts on display the logical consequences of Dirac-Wu-Yang, and Dirac-Wu-Yang are now shown to be correct,
in the special environment that gives rise to the FQHE. For, in this very special environment where electrons are chilled way down in a material which confines them to two dimensions, all of a sudden the fill factors (3.2) above emerging from Dirac-Wu-Yang with entanglement and with boson pairing of unentangled charge states are exactly what is observed. Entanglement tells us that the electrons are intimately connected with their environment and it should not be too much of a conceptual leap to connect this to the "collective" "many-body" approach of condensed matter physics. As a matter of scientific openness and discourse, these results should certainly be made known so that there is an opportunity for these connections to be understood and tightened.
So, in the end, gauge theory taken together with entanglement is shown to have the power to explain a phenomenon in condensed matter land which E. Weinberg and others do not yet understand it has the power to do.
I live to fight another day!
I do want to say one other thing, now that I am disclosing openly that Erick Weinberg is the person with whom I have been "arguing" about my work for the past year and a half, trying to be allowed in past the "gate" that he and his colleagues maintain about the physics fortress. He is the person with whom I spent 90 minutes talking at the APS meeting in April. And I have so far not convinced him of anything, but he has convinced me that he will be unremittingly critical and this is of inestimable value to me. That is why I keep going back for what I expect will be more harsh critique. I respect that, and I know that that is the only way to ultimately learn how to present my work in a way that it will start to be recognized. Baryons
are the magnetic monopoles of Yang-Mills gauge theory and one day that will be known by every student who takes nuclear physics 101; but Weinberg showed me that it is the t'Hooft-Polyakov version of the Yang-Mills monopole and the scalar fields which provide stability to these monopoles that I have been talking about all along, which I need to make the pedagogically clear. And he has now shown me that I have to lay out a sensible path for people wearing field theory hats and condensed matter hats to understand my FQHE results and how they cross between these two areas for which they believe "at the most fundamental level there is no issue." With all due respect, at the most fundamental level, there is a deep connection.
Jay

