Evidence that QM does not violate Bell's inequalities

[minkwe]

In recent threads, I have provided in great detail, crystal clear arguments why QM does not violate Bells inequalities. The summary of the conclusion is that the terms in the inequality are not the same as the ones usually calculated from QM or experiments in order to proclaim violation. Therefore, since the basis of Bell's theorem fails, that takes down Bell's theorem with it.

In this post, I will show how to calculate the correct correlations for the terms in the Bell's inequality, from experiments. The same procedure can be repeated for the 4-term CHSH inequality, although I will use the 3-term version here for simplicity:

Bell's inequality is the following:
,
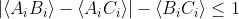
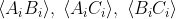
which makes use of the three terms all defined for the same set of outcomes .

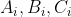
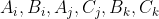
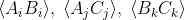
The terms from experiments are each calculated from 3 separate sets of outcomes: yielding the three terms . As I have argued in the other thread, these terms do not have the same values as those in the original inequality, therefore we are not allowed to use the QM predictions for these terms in Bell's inequality as is customarily done to demonstrate violation by QM or Experiments. In other words, the common procedure of calculating
,

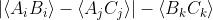
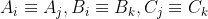
from QM and experimental data to proclaim violation of Bell's inequality is a farce. One other thing I argued in the other threads is that, we could be allowed to use those terms if and only if we can demonstrate that they are statistically equivalent through rearrangements. This ensures that must hold. Only under this condition are we allowed to use the QM prediction, and experimental results in Bell's inequality, and only under this condition do the original inequalities, derived on a single set, apply to data measured on disjoint sets. As I argued in the other thread, given 3 statistically independent sets of N outcome pairs, it is not possible to do such rearrangement in order to demonstrate the above equivalences. 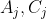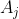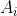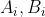To summarize why, note that we could perform row permutations of the set of outcomes so that the column matches the column of the set. 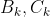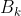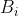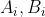Then we could do row permutations of the set of outcomes so that the column matches the column of the set. 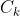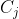One more rearrangement and we are home, since only the and pairs have not been matched. 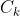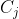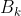But, since only row permutations are allowed, any rearrangements to make match will undo the match between and . 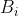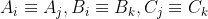Therefore, it is not possible for 3 statistically independent sets of outcome pairs to satisfy simultaneously. 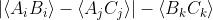Therefore the inequality does not apply, and the QM predictions for can not possibly be the same as the QM prediction for . 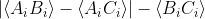Therefore it is not surprising that QM or even LHV theories would have different predictions for those terms.

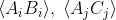
It turns out there is an even simpler way to illustrate the point. A method that can even be applied to existing experimental data, without repeating any experiments. You will note that the 3 statistically independent 2xN sets sets of outcomes are overdetermined. All you need is to measure on two sets . This is how we do it. Measure just , that will give you 2 terms , then carry out the row permutations such that . 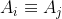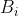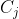Then use the rearranged together with to calculate the last term . 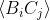If the QM predictions for the separate independent sets of outcomes should be the same as those for the single set of outcomes, then it follows that . 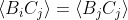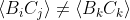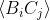But if you do this procedure, you will find that and the resulting value for will not violate Bell's inequality. Therefore, there is no justification to conclude that QM or experiments violate Bell's inequalities. Nothing can.

I encourage anyone in doubt, to go get some experimental data which matches QM (or generate one) and test this out.

[FrediFizzx]

It is easy to see by simple inspection that if the terms in the 3-term inequality are independent that the absolute bound is 3.

|-1 - (1)| -(-1) = 3

For QM I would expect the bound to be,

|-0.707 - (0.707)| -(-0.707) = 2.12

Does QM or anything physical ever violate that bound? No, since it is mathematically impossible. Just like it is mathematically impossible for anything to violate the bound of 1 when the terms are dependent as so configured in Bell's inequality.

[Guest]

It turns out there is an even simpler way to illustrate the point. A method that can even be applied to existing experimental data, without repeating any experiments. You will note that the 3 statistically independent 2xN sets sets of outcomes are overdetermined. All you need is to measure on two sets . This is how we do it. Measure just , that will give you 2 terms , then carry out the row permutations such that . Then use the rearranged together with to calculate the last term . If the QM predictions for the separate independent sets of outcomes should be the same as those for the single set of outcomes, then it follows that . But if you do this procedure, you will find that and the resulting value for will not violate Bell's inequality. Therefore, there is no justification to conclude that QM or experiments violate Bell's inequalities. Nothing can.

You are right that the rearranged data won't violate Bell's inequalities. But what you are doing here, is actually confirming Bell's theorem. Bell says that QM says that the observed pairs can't be thought of as part of completed triples. If a local hidden variables model were true, it would be possible to complement each pair, e.g, A_i, B_i, with a third element, in that case C_i, without changing the correlations (in the limit of N goes to infinity). So QM and LHV are incompatible.

Your argument actually is a rather neat proof of Bell's theorem. Very neat indeed!

[Joy Christian]

So QM and LHV are incompatible.

That is indeed a myth that has been sustained for 50 years by dirty politics and overt brainwashing. It is, however, nothing but a myth: http://rpubs.com/jjc/84238.

See also the theorem on page 12 of this paper: http://arxiv.org/abs/1201.0775 (as well as further details on this page: viewtopic.php?f=6&t=115&start=30#p3977).

[minkwe]

It turns out there is an even simpler way to illustrate the point. A method that can even be applied to existing experimental data, without repeating any experiments. You will note that the 3 statistically independent 2xN sets sets of outcomes are overdetermined. All you need is to measure on two sets . This is how we do it. Measure just , that will give you 2 terms , then carry out the row permutations such that . Then use the rearranged together with to calculate the last term . If the QM predictions for the separate independent sets of outcomes should be the same as those for the single set of outcomes, then it follows that . But if you do this procedure, you will find that and the resulting value for will not violate Bell's inequality. Therefore, there is no justification to conclude that QM or experiments violate Bell's inequalities. Nothing can.

You are right that the rearranged data won't violate Bell's inequalities. But what you are doing here, is actually confirming Bell's theorem.

Wrong! We've gone through this process already.

Here is the question: Please demonstrate that QM violates Bell's inequality


In other words, please provide the QM predictions for the terms



As you will notice once you start producing the QM predictions for those terms, you will have to make a hidden assumption in order to answer those questions. It turns out it is that hidden assumption which is wrong. If you haven't figured it out yet from the other threads and my earlier post, I'll wait until you answer those questions before telling you. You will note that the assumption has nothing to do with LHV theories, since the question is about QM predictions.

Your argument actually is a rather neat proof of Bell's theorem. Very neat indeed!

Nope it is not. I realize that without careful thought, one might make that conclusion. But remember, Bell's theorem says if QM is accurate, then no LHV theory can reproduce the QM predictions.. The problem with that is very simple. QM is accurate, as has been demonstrated by experimental measurements. But Bell did not use the correct QM predictions for the terms in the inequality in order to draw his conclusion. More precisely, it should be
if QM is accurate, and Bell and his followers are using the correct QM predictions for the situation represented by the inequalities, then no LHV theory can reproduce the QM predictions.
My argument proves that the QM predictions used by Bell and his followers is the wrong one. Therefore the correct QM predictions are completely consistent with LHV theories. In fact, it goes further to prove that it is impossible to violate the inequalities.

Bell says that QM says that the observed pairs can't be thought of as part of completed triples. If a local hidden variables model were true, it would be possible to complement each pair, e.g, A_i, B_i, with a third element, in that case C_i, without changing the correlations (in the limit of N goes to infinity).

Now there is a grave temptation for those who love non-locality or other spooky business to say, but LHV requires those rearrangements to be possible. That couldn't be further from the truth. You say if LHV is true, it would be possible to complement each entry to have a set of triples for each particle pair. But that is not what you are doing, you are trying to complement the pair you measured with with from a different pair. Why would you expect the triple to exist in the outcomes if you only ever measure two entries on independent particle pairs!? That is the problem. The argument shows that you should not expect the joint probability distribution to exist in data in which you only measured pairs on statistically independent sets of particles. Even if LHV theories are at play.

Let me remind you of the crux of the argument:

given 3 statistically independent sets of N outcome pairs, it is not possible to do such rearrangement in order to demonstrate the above equivalences. To summarize why, note that we could perform row permutations of the set of outcomes so that the column matches the column of the set. Then we could do row permutations of the set of outcomes so that the column matches the column of the set. One more rearrangement and we are home, since only the and pairs have not been matched. But, since only row permutations are allowed, any rearrangements to make match will undo the match between and . Therefore, it is not possible for 3 statistically independent sets of outcome pairs to satisfy simultaneously.

It does not matter what the source of the sets of outcomes is. This is an impossibility proof, which essentially highlights the statistical tautology: 3 statistically independent sets are not statistically dependent. This is true for LHV just as well as QM and experimental data. This would have been obvious for those who understand statistics but it has been carefully obscured for decades simply because Bell left out indices from his terms, giving the false impression that . And even to this day, many do not see it.

Therefore it is clear that my argument is not a reaffirmation of Bell's theorem, but a solid refutation of it.

[Guest]

Here is the question: Please demonstrate that QM violates Bell's inequality . In other words, please provide the QM predictions for the terms . As you will notice once you start producing the QM predictions for those terms, you will have to make a hidden assumption in order to answer those questions. It turns out it is that hidden assumption which is wrong. If you haven't figured it out yet from the other threads and my earlier post, I'll wait until you answer those questions before telling you. You will note that the assumption has nothing to do with LHV theories, since the question is about QM predictions.

The QM predictions rely only on the standard interpretation of the quantum mechanics formalism and the particular choices of measurements and state. The calculations are carried out in full detail and by brute force in, for instance, Burkhard Kümmerer and Hans Maassen (1988), "Elements of Quantum Probability", Quantum Probability Communications, X 73-100, eds. R.L. Hudson, J.M. Lindsay, World Scientific, http://www.math.ru.nl/~maassen/papers/elements.pdf page 16.

You can find sketches of the calculations in Ballentine's 1998 book "Quantum mechanics: a modern development" (World Scientific) p. 586 or in Asher Peres' 2002 book "Quantum Theory: Concepts and Methods" (Kluwer) p. 162.

We can work together through the arguments in one of these sources, if you like.

The main ingredient is the following. Suppose we have a bipartite quantum system in a (pure) state Psi. So we have two complex Hilbert spaces H and K, and a unit length vector Psi in H otimes K (by "otimes" I mean "tensor product"). Suppose we measure observable A on subsystem H and observable B on subsystem K. The observables A and B are, mathematically, self-adjoint operators on H and K respectively. Then the expectation value of the product of the outcomes of measuring A and B is < Psi | A otimes B | Psi >.

Which means to say that if the state is prepared and measured N times in the same way, each time resulting in measurement outcomes equal to one of the eigenvalues of A and one of the eigenvalues of B, and one averages the product of those outcomes, and lets N go to infinity, the result converges to < Psi | A times B | Psi >.

In more detail, if [ a ] is the eigenspace of A corresponding to eigenvalue a, and similarly for the other observable, then the chance that the measurement of A yields a and the measurement of B yields b is the squared length of the projection of the state vector | Psi > into the subspace [ a ] otimes [ b ] of H otimes K. This is the Born rule, in its modern form, applied to joint measurements on a multipartite system.

The expectation value of the product of the outcomes is the sum over a and b of a times b times the just mentioned probability. A little bit of algebra gives the usual formula < Psi | A times B | Psi > for the expectation value.

The Born rule is the key interpretational tool in quantum mechanics: when you prepare a system in state ... and then measure ... , the probability of getting ... is .... That's all we have.

I wonder if you have difficulties with the specific choice of Psi, A and B and the ensuing calculations, or with the Born rule. I wonder what is the assumption which you think is hidden in the formalism and the calculations.

[Guest]

It does not matter what the source of the sets of outcomes is. This is an impossibility proof, which essentially highlights the statistical tautology: 3 statistically independent sets are not statistically dependent. This is true for LHV just as well as QM and experimental data. This would have been obvious for those who understand statistics but it has been carefully obscured for decades simply because Bell left out indices from his terms, giving the false impression that . And even to this day, many do not see it.

I am not aware of any proof of Bell's theorem which relies on such an obviously wrong claim. Of course statistically independent sets of data are statistically independent of one another.

Perhaps it could be useful to look at a proof of Bell's theorem (incompatibility of QM and PHV) which does not use Bell's inequality at all. Steve Gull proves Bell's theorem using Fourier analysis. See http://www.mrao.cam.ac.uk/~steve/maxent2009/ and http://www.mrao.cam.ac.uk/~steve/maxent2009/images/bell.pdf.

And regarding the traditional proofs: Bell (1981) writes "Sufficiently many repetitions of the experiment will allow tests of hypotheses about the joint conditional probability distribution P(A,B|a, b) for results A and B at the two ends for given signals a and b." Bell's point being that many repetitions of the experiment with given settings a and b, allow one to determine P(A,B|a, b) up to some statistical error, which can be made as small as you like if you do enough repetitions. The derivation of the CHSH inequality, which concerns theoretical relations between the theoretical values P(A,B|a, b) for various values of a and b, does not refer to any sequence of actual experiments at all! It certainly doesn't make any assumptions that Ai = Aj or whatever.

[minkwe]

I am not aware of any proof of Bell's theorem which relies on such an obviously wrong claim. Of course statistically independent sets of data are statistically independent of one another.

If you are not aware of it, then you are uninformed. Otherwise, answer the question I asked you earlier and let us find out

Here is the question: Please demonstrate that QM violates Bell's inequality

by providing , the QM predictions for the terms

[FrediFizzx]

Here is the question: Please demonstrate that QM violates Bell's inequality

by providing , the QM predictions for the terms

I predict that all you will get as an answer is more subterfuge.

[Joy Christian]

Here is the question: Please demonstrate that QM violates Bell's inequality

by providing , the QM predictions for the terms

I predict that all you will get as an answer is more subterfuge.

I am not sure that they are even aware of the fact that they are being evasive. They are a victim of over 50 years of brainwashing and political control by the elite.

[minkwe]

Here is the question: Please demonstrate that QM violates Bell's inequality

by providing , the QM predictions for the terms

I predict that all you will get as an answer is more subterfuge.

I am not sure that they are even aware of the fact that they are being evasive. They are a victim of over 50 years of brainwashing and political control by the elite.

For some reason such a simple question, which Bell answered without blinking, is scaring the bejeebers out of Bell's followers. Perhaps because they now get a hint that they've sold all their property and bought a field in which there is no gold burried, like they had hoped. As you read the Bell papers, you will find the error everywhere. Simply introduce the subscripts where they've left them out and watch everything crumble. For example, equation (1) of Weihs paper here: http://arxiv.org/pdf/quant-ph/9810080v1.pdf, and the paragraph after it.

Or equations 14-17 of Bell's own later paper, https://cds.cern.ch/record/142461/files/198009299.pdf. After 14 years he hadn't learnt a thing. Though some authors believe, he may have smelled the coffee in 1990 not long before his death, http://philsci-archive.pitt.edu/11268/2/Bell_final.pdf

But let's not permit them any reprieve. Here is the example I gave previously which makes the issue as crystal clear as possible. This time, we will include the subscripts:

It is well known that in an experiment in which a single coin is tossed, the probability of obtaining and obeys the relationship . But the usual discussion about coin tosses, in which we toss it on a table or floor and read the pre-existing side is too contrived. Think instead of the following we have two devices into which we toss the coin. One is a H-reading device and the other is a T-reading device. Say for example that the devices each have an LED which illuminates if the appropriate side of the coin is UP, but does not illuminate otherwise. Let us use just the H-reading device, toss our coin N times, and every time the light illuminates we increment our count and every time device does not illuminate, we increment out count. At the end we calculate the relative frequencies and , we will find that the relationship holds. We can repeat this procedure using just the T-reading device and still verify the same relationship holding exactly . But what if we do two separate experiments and. First toss our identical types of coins N times into the H-reading device, and from that calculate just , and N times into the T reading device and from that calculate just ? It would be quite naive to think that the relationship continues to hold. In fact, such a scenario can violate the relationship drastically, up to .

Bell Follower Responds:

Only if you assume that your 'identical' coins don't in fact have the same probability distribution. In which case, yes, you could violate the inequality, by say having two types of coins, one for which P(H) is approximately one (and hence, P(T) is approximately 0), and the other for which P(T) is approximately one, and P(H) approximately zero. But you'd have to make sure only to throw the first kind of coin into the H-reading device, and the second kind of coin into the T-reading device; in a Bell test, however, the nature of the device will only be decided once the coin is already in the air, and it's not hard to see that in this case, always P(T) + P(H) = 1(at least up to statistical error)

I very much expected that they will swallow the trap hook and sinker and boy did they. It was very easy to show that even if the coins thrown into both machines each time were identical, we would have a violation if the machines were not simply static readers of the coins. For example, let us assume that the coins were not biased to start with, ie by considering the properties of the coins by themselves P(T) = P(H) = 0.5. But say the machines are biased in the way they read the coins such that the H-reading machine is always 25% more likely to report H and the T-reading machine is always 25% more likely to report T. In this case, toss a fair coin into the T reading machine would give us , and tossing a fair coin into the H-reading machine would give us . But now if we only take the H-outcomes from the H-reading machine, and the T-outcomes from the T-reading machine, we now have an apparent violation. Would we conclude that our coins are not local realistic? Would we conclude that there is some spooky action taking place, or would we simply sweep the subscripts under the rug and say local realism implies but experiment shows , therefore mystery. If we are smart we will realize that the existence of a joint probability distribution P(H,T) for a given coin prior to measurement, does not guarantee that such a joint PD can be reconstructed from measurement outcomes, if we measure each outcome by itself in separate experiments. Therefore it is not correct to equate all the expectation values as was done to derive Bell's theorem. Bell's theorem is dead!

For the Bell believers reading this, assuming you are not converted yet, now you know the truth. If you want to keep spreading the falsehood that is Bell's theorem, I have just one request, include the subscripts in all your terms, or your pants (trousers if you like) will go up in flames.

[FrediFizzx]

It is pretty mind boggling that Bell's theorem has been mainstream for over 50 years and that people didn't see that nothing can violate the inequalites. Mathematically impossible.

[Joy Christian]

It is pretty mind boggling that Bell's theorem has been mainstream for over 50 years and that people didn't see that nothing can violate the inequalites. Mathematically impossible.

Some people did see, very early on, that nothing can violate the inequalities.

For example Clauser --- the "C" of the CHSH inequality --- was absolutely convinced (so I was told by my former PhD advisor, Abner Shimony --- the "S" of the CHSH inequality) before his very first experiment with Freedman that theirs will be a truly revolutionary experiment and will prove that quantum mechanics is actually wrong by not exhibiting the strong correlations. He was convinced of this because he (and the other pioneers) were well aware of the fact that nothing can violate the inequalities. Shimony, however, was convinced that the experiment will exhibit the strong correlations, thus exhibiting a refutation of local realism rather than quantum mechanics. Clauser was genuinely surprised (so I was told by Shimony) when he witnessed the strong correlations in his 1970's experiment with Freedman.

[minkwe]

It is pretty mind boggling that Bell's theorem has been mainstream for over 50 years and that people didn't see that nothing can violate the inequalites. Mathematically impossible.

Fred, as Joy says, indeed some people saw early on. Worse, Boole had argued as much 100+ years before Bell.

For example Clauser --- the "C" of the CHSH inequality --- was absolutely convinced (so I was told by my former PhD advisor, Abner Shimony --- the "S" of the CHSH inequality) before his very first experiment with Freedman that theirs will be a truly revolutionary experiment and will prove that quantum mechanics is actually wrong by not exhibiting the strong correlations.

Once they assumed the expectation values predicted by QM and measured for the experiment were the same as those in the inequality, there was no way out of the pit. Not many people have yet realized the subtle difference between the two. Clauser was right to be convinced nothing could violate it. But he was wrong to think it meant QM was wrong.

Shimony, however, was convinced that the experiment will exhibit the strong correlations, thus exhibiting a refutation of local realism rather than quantum mechanics. Clauser was genuinely surprised (so I was told by Shimony) when he witnessed the strong correlations in his 1970's experiment with Freedman.

As for Shimony, he was right that the experiment would exhibit strong correlations but, he was wrong to think it implied refutation of local realism. Between the two of them, they had parts of the truth, but they were pointing fingers at QM on the one hand and local realism on the other, meanwhile the culprit was themselves (and Bell) all along. They should have realized that both QM and local realism were correct, but they were wrong in their calculations attempting to demonstrate violation.

On the other hand, I think I can safely say that nobody understands quantum mechanics.
-- Richard P. Feynman 1964

I can safely say nobody who believes Bell's theorem understands quantum mechanics or statistics or arithmetic for that matter.

It is actually quite funny to read Bell's paper against von Neumann's no-go theorem and see him present exactly the same argument which sinks his own theorem, only to publish his own no-go theorem a year later! For example in his book From Physics to Philosophy, Jeremy Butterfield, presents it like so:

What Bell objects to in both von Neumann's and Kochen and Specker's no-go theorems is arbitrary assumptions about how the results of measurements undertaken with incompatible experimental arrangements would turn out. For von Neumann, it is the assumption that if an observable C is actually measured, where and , then had A instead been measured, or B, their results would have been such as to sum to the value actually obtained for C. For Kochen and Specker, who adopt von Neumann's linearity requirement only when , it is the assumption that the results of measuring C would be the same independent of whether C is measured along with A and B or in the context of measuring some other pair of compatible observables A' and B' such that C = A' + B'. What makes these assumptions arbitrary, for Bell, is that the results of measuring observables A,B,C, ... might not reveal separate pre-existing values for them, but rather realize mere dispositions of the system to produce those results in the context of specific experimental arrangements they are obtained in. In other words, the 'observables' at issue need not all be beables in the hidden-variables interpretations the no-go theorems seek to rule out.

The coin-reading machine example I gave above also could be used to visualize what is happening here. is not a property of a beable of the coin. It is merely reveals the disposition of the system (coin + machine) to produce those results in the specific context of the experiment.

[FrediFizzx]

Joy recently mentioned a meeting he had with Lucien Hardy (would have liked to been a fly on the wall for that meeting ) so I was looking at some of Dr. Hardy's papers. This one drew my interest.

http://arxiv.org/abs/1203.1352 , "Logical Bell Inequalities"

I contend that his eq. (1) has to be wrong.



Should simply be.



So where exactly does the flaw creep in if I am right? The reason I think it is wrong because simple inspection for say N = 4 shows that we could have |1 + 1 + 1 +1| = 4 not 4 - 2 = 2.

[Joy Christian]

Good question, Fred. Perhaps Michel will have a look at Lucien's paper to pinpoint the error.

Let me also mention that I received the following email a few days ago from an extremely well known and talented string theorist. You can narrow down the name to a handful of people, but I am not revealing his identity publicly because this was a private correspondence.

Dear Joy,

Thanks for pointing out your paper.

If I understand correctly, your paper contradicts the Clauser-Horne inequality for hidden variables, whose proof is rather simple.

I would advise you to go over the proof of the theorem with your model in order to find where the mistake is, either in the
theorem or (more likely, in my mind) in your counter example.

Regards,

[Name]

This is the usual response from nearly everyone who has ever looked at my work. Despite the explicit and simple counterexample I have presented over the past eight years, the usual attitude of people is that my model "must be wrong" because the proofs of Bell-type inequalities are so simple. And the disingenuous criticism of my model by non-physicists like Gill hasn't helped. What the critics don't seem to realize is that these inequalities are logically correct and simple, but they have nothing to do with physics. It is therefore not at all surprising that they are routinely "violated" in the actual experiments. The same is true of Lucien's "logical Bell inequality."

[FrediFizzx]

Good question, Fred. Perhaps Michel will have a look at Lucien's paper to pinpoint the error.

Let me also mention that I received the following email a few days ago from an extremely well known and talented string theorist. You can narrow down the name to a handful of people, but I am not revealing his identity publicly because this was a private correspondence.

Dear Joy,

Thanks for pointing out your paper.

If I understand correctly, your paper contradicts the Clauser-Horne inequality for hidden variables, whose proof is rather simple.

I would advise you to go over the proof of the theorem with your model in order to find where the mistake is, either in the
theorem or (more likely, in my mind) in your counter example.

Regards,

[Name]

This is the usual response from nearly everyone who has ever looked at my work. Despite the explicit and simple counterexample I have presented over the past eight years, the usual attitude of people is that my model "must be wrong" because the proofs of Bell-type inequalities are so simple. And the disingenuous criticism of my model by non-physicists like Gill hasn't helped. What the critics don't seem to realize is that these inequalities are logically correct and simple, but they have nothing to do with physics. It is therefore not at all surprising that they are routinely "violated" in the actual experiments. The same is true of Lucien's "logical Bell inequality."

Well, I woudn't expect a string theorist to care very much about Bell's "theorem". Someone in the field like Dr. Hardy is in is certainly going to care more about your work. But after reading this paper, I am really curious about how he gets eq. (1) with no dependency between the terms. And in Sect. B. "A Curious Observation", he seems to contradict himself in note [17]. Since p_i can be 1, then for sure the sum can be N. Not N -1. ???

There is no way that eq. (1) can be true without dependency between the terms. There is really nothing "curious" at all.

[Joy Christian]

But after reading this paper, I am really curious about how he gets eq. (1) with no dependency between the terms. And in Sect. B. "A Curious Observation", he seems to contradict himself in note [17]. Since p_i can be 1, then for sure the sum can be N. Not N -1. ???

There is no way that eq. (1) can be true without dependency between the terms. There is really nothing "curious" at all.

Their argument certainly looks very confusing. They do seem to acknowledge the "puzzle", however, on the top of page 3. You seem to have it right as far as I can see.

[FrediFizzx]

But after reading this paper, I am really curious about how he gets eq. (1) with no dependency between the terms. And in Sect. B. "A Curious Observation", he seems to contradict himself in note [17]. Since p_i can be 1, then for sure the sum can be N. Not N -1. ???

There is no way that eq. (1) can be true without dependency between the terms. There is really nothing "curious" at all.

Their argument certainly looks very confusing. They do seem to acknowledge the "puzzle", however, on the top of page 3. You seem to have it right as far as I can see.

If you get a chance, you should ask Dr. Hardy about this. Anyways, back to the topic of this thread, this is an example of how the myth that QM can "violate" the inequalities gets further spread thoughout the mainstream.

[Guest]

But after reading this paper, I am really curious about how he gets eq. (1) with no dependency between the terms. And in Sect. B. "A Curious Observation", he seems to contradict himself in note [17]. Since p_i can be 1, then for sure the sum can be N. Not N -1. ???

There is no way that eq. (1) can be true without dependency between the terms. There is really nothing "curious" at all.

Their argument certainly looks very confusing. They do seem to acknowledge the "puzzle", however, on the top of page 3. You seem to have it right as far as I can see.

If you get a chance, you should ask Dr. Hardy about this. Anyways, back to the topic of this thread, this is an example of how the myth that QM can "violate" the inequalities gets further spread thoughout the mainstream.

There is dependency between the terms: it is *assumed* that Phi = phi_1 & phi_2 & ... & phi_N is impossible.

To give an example: suppose a local hidden variables model is true in the Bell-CHSH set-up. Define X_1 and X_2 to be the outcomes which Alice would have observed, had she used either of her two settings 1 or 2 (outcomes +/- 1 in the conventional scenario), define Y_1 and Y_2 to be the outcomes which Bob would have observed, had he used either of his two settings 1 or 2 (outcomes +/- 1 in the conventional scenario).

Notice that (since these four variables are restricted to being equal to +/- 1) it is impossible that X_1 = Y_1 & X_1 != Y_2 & Y_2 != X_2 & X_2 != Y_1. For instance if X_1 = Y_1 = +1, then Y_2 would have to be -1, X_2 would have to be +1, and Y_1 would have to be -1 ... a logical contradiction. Similarly in the other case X_1 = Y_1 = -1.

It follows that Prob(X_1 = Y_1) + Prob(X_1 != Y_2) + Prob(Y_2 != X_2) + Prob(X_2 != Y_1) <= 3.

The point is that these variables X_1, X_2, Y_1, Y_2 exist according to a local hidden variables theory, but quantum mechanics says nothing about them at all. In QM we don't assume they exist at all.

Quantum mechanics does predict the value of Prob(Alice's outcome = Bob's outcome | Alice uses setting i and Bob uses setting j) for each i, j = 1, 2. And experiment allows us to measure the value of Prob(Alice's outcome = Bob's outcome | Alice uses setting i and Bob uses setting j).

So in an experiment with many trials with each of the four pairs of settings we can get to see (up to statistical error) the values of Prob(Alice's outcome = Bob's outcome | Alice uses setting 1 and Bob uses setting 1), Prob(Alice's outcome != Bob's outcome | Alice uses setting 1 and Bob uses setting 2), Prob(Alice's outcome != Bob's outcome | Alice uses setting 2 and Bob uses setting 2), Prob(Alice's outcome != Bob's outcome | Alice uses setting 2 and Bob uses setting 1).

And QM allows the sum of these four probabilities to exceed 3. In fact, QM allows 1 + 2 sqrt 3 = 3.4 approx