Take, for example, Moldoveanu's recent blog post about my work. Evidently, the purpose of his blog post is to mislead the scientific community about my work, either deliberately, or because of his own incompetence in elementary mathematics and physics (I will come to Gill's incompetence in mathematics and physics in a minute).
Let us look at his main "argument" to see what I mean. On his blog he makes the following claim:

This travesty of my model is of course completely bogus, as anyone who has actually read my papers would recognize at once. I would not even call it a "straw-man." It is far worse than that. But I am very pleased that Moldoveanu has himself exposed his incompetence so vividly on his blog, so that we can enjoy it with a chuckle.
Let us go through Moldoveanu's mistakes (or misrepresentations) one-by-one so that there remains no ambiguity or confusion, at least in the mind of a neutral reader:
(1) Nowhere in any of my papers have I ever claimed that "it is all in the sign of
(2) In reality, my model is "all about" correlations among the points of a parallelized 3-sphere, and as such it has nothing to do with either the definition of the cross product or complex numbers. This has been pointed out to Moldoveanu, literally hundreds of times, by me as well as others, but he has learned nothing. Check out, for example, this paper, where I systematically debunk dozens of his silly claims about my model. In essence, it is the orientation of S^3 that matters, nothing else.
(3) More specifically, the definition of the cross product, as in
(4) The actual identity used in my model to represent the parallelized 3-sphere is not the one Moldoveanu claims it is used, but the following geometrical identity,
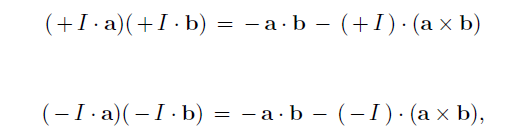
where
(5) The reason Moldoveanu remains confused about such elementary matters is because he continues to think in terms of complex numbers, which, as already noted, have nothing to do with my model. Complex numbers do not have handedness (or orientation). There is no such thing as left-handed complex numbers or right-handed complex numbers. Moreover, complex numbers are commutative numbers, whereas a parallelized 3-sphere can only be correctly represented by quaternions, which of course do not commute. A parallelized 3-sphere is a set of unit quaternions, which, in turn, is a well known solution of Einstein's field equations of general relativity.
These five points are already sufficient for anyone to recognize that Moldoveanu's claims are completely bogus. But don't take my word for it. Do check out yourself these explicit numerical computations by Albert Jan Wonnink, Fred Diether, and Michel Fodje, which expose that Moldoveanu's claims are indeed completely bogus:
http://challengingbell.blogspot.co.uk/2 ... of_30.html
http://challengingbell.blogspot.co.uk/2 ... f-joy.html
These explicit simulations complement the systematic theoretical refutations of the nonsensical claims by Moldoveanu and Gill, which are available online since 2011:
http://arxiv.org/abs/1203.2529
http://arxiv.org/abs/1501.03393 (see, especially, the derivation of the Eq. (B10) in this paper).
There is therefore no excuse for Moldoveanu and Gill to continue to make their bogus claims without paying attention to the arguments presented in these documents.
Next, Moldoveanu makes even more bizarre claim. He claims that in my model outcomes of the experiment are not represented by scalar numbers as A(a, L) = +/-1 and B(b, L) = +/-1. I find this extraordinary, because one has to be literally blind to not see A(a, L) = +/-1 and B(b, L) = +/-1 in my model, which are explicitly stated even in my one-page paper, let alone the more recent and more detailed discussion of them in Eqs. (7), (8), and (B10) in my latest reply to Gill I have linked above:

This claim by Moldoveanu is a worthless gobbledygook. It shows that his inability to understand basic physics and mathematics is not limited to his reading of my work. To begin with, what Weatherall does in his grossly misleading paper has nothing to do with my model despite his disingenuous claims. Secondly, Weatherall does not even have a "model" in his paper, let alone a valid one. What he does is so naïve that one can't help wondering how he got his professorship. Any idiot can construct a model that does not work. All Weatherall does in his paper is construct something without a head or a tail. The challenge is to construct a model that does work, with the correct implementation of statistics, such as in my model. In any event, I have thoroughly debunked Weatherall's dishonest claims about my model in this paper:
http://libertesphilosophica.info/blog/w ... hapter.pdf
What is more, as anyone who has been following my work with a positive and/or neutral attitude knows, by now there have been many explicit, even event-by-event simulations of both my original Clifford algebraic model of 2007 as well as that of a non-Clifford algebraic representation of the 3-sphere, such as this new simulation.
This brings us back to my question: Are some of the critics of my work, in particular Gill, Moldoveanu, and Weatherall, deliberately deceitful, or merely incompetent?
Now Moldoveanu seems to be just incompetent and misguided. Evidently, after Fred Diether and I have explained his mistakes to him literally hundreds of times, he still remains entirely clueless about what the hidden variable
More surprising is the fact that Gill makes the same algebraic and conceptual blunders as Moldoveanu despite the fact that he holds a professorship in mathematical statistics at a well known Dutch university. He has, however, admitted both publicly on these very pages as well as privately that he cannot do algebra. In fact, I and others have repeatedly exposed on these pages, not only his algebraic blunders, but also his duplicitous character and vested interests: (1), (2). He is evidently in the business of constantly misleading the scientific community by subterfuge. Thus there is not much of a mystery about the intentions, motivations, and actions of Gill.
Weatherall, on the other hand, is a young philosopher, also holding an academic position. I am prepared to overlook the physical and mathematical deficiencies in his "analysis" (and there are plenty), but what is astonishing is that he either deliberately or inadvertently sets out to commit one of the most elementary logical fallacies that any competent philosopher would have been extra vigilant about. He commits the straw-man fallacy so blatantly that only a true Bell believer would fall for it. Needless to say, this is outright dishonesty, designed to mislead the scientific community. He sets out to give a false impression in his paper that he is going to discuss my model for the EPR-Bohm correlation, but what he actually discusses in his paper and refutes has nothing whatsoever to do with my model. In fact what he does is nothing more than present a 50 year old trite argument by Bell and his followers which we have already seen being demolished on these pages many times over. Since I have debunked Weatherall's argument in considerable detail in the paper I have linked above, I will refrain here from discussing the duplicity of his paper once again.
Thus there is sufficient evidence to conclude that all three of the critics, Gill, Moldoveanu, and Weatherall, are deliberately deceitful and manifestly incompetent. No matter how one looks at it, it is quite evident that the only way these critics are able to criticise my model is by first replacing it with their own grotesque straw-man.


