minkwe wrote:To me, the best approach is always to write the analysis code separately of a given model, and apply the same code to all the models, including experimental data. This appears to have been your intention, and is what I have done with epr-simple and epr-clocked. You can throw the experimental data as well as data from any other model at it directly without any fiddling. The same goal-post for everyone since I no longer trust experimenters to analyze their own data.
But your analysis part is overly complicated and probably wrong for some of the models because of the way you are doing the calculations.
The equation for calculating the expectation value is:
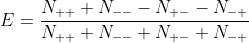
Note that there are no zero outcomes in this expression, therefore whether or not a model produces zeros, is completely irrelevant for it. If zeros are causing you problems, then you are going about it the wrong way. You should be calculating each of the paired coincidence counts

and then from that calculating the Expectation value
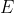
from that.
The equation that is used in Sascha's program is E = (NE - NU)/(NE + NU).
That's equal to ((N++ + N--) - (N+- + N-+)/((N++ + N--) + (N+- + N-+)), provided that the zero events are removed. Now for those zero events, I could have called my routine removeZero detectionLoophole, because that's what it is. You can pass the data through this loophole three ways:
My way, remove them after they have been created by the event generator
Michel's way, don't allow them to be picked at all
Joy's way, use the R routine length((A*B)[A & B]) which gets rid of them by selecting products where A and B are non zero
All these will give equal results. Which is best? My method lets me see what effect removing zeros has, and therefore what effect the detection loophole has on the simulation.

