SciPhysicsForums.com

***
After Fred's recent post about my derivation of the upper bound on CHSH, we have been trying to better understand why the upper bound on CHSH is 2\/2 and not 4 ?

In fact I have already answered this question much more rigorously in this paper, but perhaps a simplified explanation is called for, especially because the underlying geometrical reason for the bound 2\/2 instead of 4 is quite straightforward. In particular, it has nothing to do with any mystical notion such as "quantum non-locality."

As in Fred's post linked above, we begin with the square of the CHSH-type string of the (geometric) products of the standardized variables (or standard scores):

,

where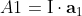 , , 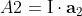, 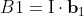and 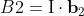are unit bivectors about the directions 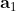, , , 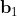and 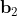, with 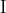being the volume form.

Now in Fred's post as well as in my original derivation, the upper bound of 2\/2 on CHSH is derived by using the assumption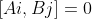 , justified on the physical grounds that 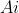and 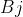are space-like separated, and there does not exist a "third" particle in the EPR-B type experiment that can be detected along the exclusive direction 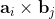in addition to the detections of the pair of particles along the directions 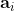and 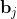. This permits some rearrangement in the 16 terms, leading to the maximum value of 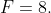Consequently, the upper bound on the CHSH in this case turns out to be 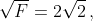for the four Bell test directions (or angles).

So far so good. But can we do better? Is it possible to increase the upper bound on CHSH to its apparent full potential of 4 ? And if not, then why not? Evidently, this seems to be possible if we can arrange a maximum value of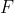 to be 16. Then we would have 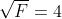as desired. Now from the above expansion of 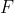it is clear that we can have 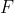= 16 if each of its 16 terms equals to +1. Is that possible? A little reflection will convince you that it is possible provided we can have all four of the directions 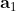, , , 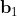and 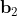orthogonal to each other. But one cannot have four directions orthogonal to each other in a three dimensional space such as R^3.

So there. One cannot have all four directions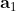 , , , 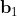and 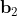orthogonal to each other in R^3. And therefore we cannot extend the upper bound on CHSH to 4.

The maximum value of the upper bound on CHSH within R^3 is 2\/2. Therefore the observed upper bound on CHSH is 2\/2. It has nothing to do with any mystical idieas like quantum entanglement or non-locality. It is simply a numerical constraint arising form the geometrical and topological properties of the physical space we live in.

In fact, |CHSH| 4 is physically not possible even within S^3, which is locally (or tangentially) just R^3. The only way to get the bound |CHSH| 4 is to have most of the observation directions orthogonal to each other, i.e., have a topology stronger than S^3, as shown in the last plot of this simulation: http://rpubs.com/jjc/84238.

Joy Christian

Here is a simple relationship among bivectors that may help to understand the above argument. Consider four bivectors about four distinct directions , , , and . Then the following relationship among them is easy to prove by repeated application of geometric product (here all vectors are unit vectors, and so are all bivectors):

Here are the results of a small simulation experiment. For each of the four setting pairs I generated one pair of measurement outcomes. They happened to be as follows:
a, b: +1, +1
a, b': +1, -1
a', b: -1, +1
a', b': +1, -1
I find correlations +1, -1, -1,-1 and CHSH = 4 which is much larger than 2 sqrt 2.

Please explain. Clearly, this pattern could just as well continue for much larger numbers of measurements. It is always possible to get CHSH = 4. It is always possible to get CHSH = -4. With many, many observations one can get values in between, spread out as evenly as you like.

Guest wrote:Here are the results of a small simulation experiment. For each of the four setting pairs I generated one pair of measurement outcomes. They happened to be as follows:
a, b: +1, +1
a, b': +1, -1
a', b: -1, +1
a', b': +1, -1
I find correlations +1, -1, -1,-1 and CHSH = 4 which is much larger than 2 sqrt 2.

Please explain. Clearly, this pattern could just as well continue for much larger numbers of measurements. It is always possible to get CHSH = 4. It is always possible to get CHSH = -4. With many, many observations one can get values in between, spread out as evenly as you like.

Wonderful. There is no mystery here that needs to be explained. If you consider four independent pairs of measurement outcomes as you have considered, then it is always possible to get , as you have observed.

The mystery that cries out for explanation is this: Why has no one ever observed CHSH greater than 2 sqrt 2 in any quantum mechanical experiment? Not just for the singlet state in EPR-Bohm type experiments, but for any quantum mechanical state, no matter how complicated. It is this physical mystery that is explained above.

Guest wrote:Here are the results of a small simulation experiment. For each of the four setting pairs I generated one pair of measurement outcomes. They happened to be as follows:
a, b: +1, +1
a, b': +1, -1
a', b: -1, +1
a', b': +1, -1
I find correlations +1, -1, -1,-1 and CHSH = 4 which is much larger than 2 sqrt 2.

Please explain. Clearly, this pattern could just as well continue for much larger numbers of measurements. It is always possible to get CHSH = 4. It is always possible to get CHSH = -4. With many, many observations one can get values in between, spread out as evenly as you like.

What are you using for the CHSH inequality? Here's an easy explanation of the inequality. Suppose I have two sets of measurements, A, B and A', B'. Then the CHSH inequality is:



Since the measurements must all be +1 or -1 the value of M is always equal to plus or minus 2. This can be easily seen by rewriting M as:



When averaging over a large number of experiments, we obtain M greater than or equal -2 and less than or equal 2. That's all there is to it.

jreed wrote:

Guest wrote:Here are the results of a small simulation experiment. For each of the four setting pairs I generated one pair of measurement outcomes. They happened to be as follows:
a, b: +1, +1
a, b': +1, -1
a', b: -1, +1
a', b': +1, -1
I find correlations +1, -1, -1,-1 and CHSH = 4 which is much larger than 2 sqrt 2.

Please explain. Clearly, this pattern could just as well continue for much larger numbers of measurements. It is always possible to get CHSH = 4. It is always possible to get CHSH = -4. With many, many observations one can get values in between, spread out as evenly as you like.

What are you using for the CHSH inequality? Here's an easy explanation of the inequality. Suppose I have two sets of measurements, A, B and A', B'. Then the CHSH inequality is:



Since the measurements must all be +1 or -1 the value of M is always equal to plus or minus 2. This can be easily seen by rewriting M as:



When averaging over a large number of experiments, we obtain M greater than or equal -2 and less than or equal 2. That's all there is to it.

The mistake they made is in their last a', b' results. a' in the third one is -1 and it is +1 in a', b'. So they are really doing a, a', a'' or a1, a2, a3. You can get 4 if you do that. Otherwise CHSH greater than 2 is mathematically impossible. QM, etc. don't really violate CHSH as seen by Michel's explanation.

jreed wrote:What are you using for the CHSH inequality? Here's an easy explanation of the inequality. Suppose I have two sets of measurements, A, B and A', B'. Then the CHSH inequality is:



Since the measurements must all be +1 or -1 the value of M is always equal to plus or minus 2. This can be easily seen by rewriting M as:



When averaging over a large number of experiments, we obtain M greater than or equal -2 and less than or equal 2. That's all there is to it.

The above argument is fundamentally flawed, as Fred has explained above. The elementary mistake in it is the same mistake that Gill et al. keep making, and it is the same mistake that all Bell devotees keep making. It has been repeatedly explained on these pages, especially by "minkwe." See viewtopic.php?f=6&t=181#p4912.

I have explained the mistake in the above argument in my own way in this paper. See, especially, Eqs. (12) to (26). In essence the seemingly innocent step from the first expression above to the second by "rewriting M" is a cheat. Physically it is nonsense, as I have explained in my paper. All experiments to date have rejected it.

More specifically, the correct expression of M is actually the following:

.

The cheat in the above argument is in surrupticiouly replacing this sum of four separate averages with the following single average:

.

Without this replacement the last step does not follow. But this innocent looking replacement is not justified for the physical experiments, as explained in my paper.

Joy Christian wrote:

jreed wrote:What are you using for the CHSH inequality? Here's an easy explanation of the inequality. Suppose I have two sets of measurements, A, B and A', B'. Then the CHSH inequality is:



Since the measurements must all be +1 or -1 the value of M is always equal to plus or minus 2. This can be easily seen by rewriting M as:



When averaging over a large number of experiments, we obtain M greater than or equal -2 and less than or equal 2. That's all there is to it.

The above argument is fundamentally flawed, as Fred has explained above. The elementary mistake in it is the same mistake that Gill et al. keep making, and it is the same mistake that all Bell devotees keep making. It has been repeatedly explained on these pages, especially by "minkwe." See viewtopic.php?f=6&t=181#p4912.

I have explained the mistake in the above argument in my own way in this paper. See, especially, Eqs. (12) to (26). In essence the seemingly innocent step from the first expression above to the second by "rewriting M" is a cheat. Physically it is nonsense, as I have explained in my paper. All experiments to date have rejected it.

More specifically, the correct expression of M is actually the following:

.

The cheat in the above argument is in surrupticiouly replacing this sum of four separate averages with the following single average:

.

Without this replacement the last step does not follow. But this innocent looking replacement is not justified for the physical experiments, as explained in my paper.

In your so-called correct expression M will always tend to zero. Recall that in EPR experiments, Alice and Bob are free to choose the angles of their detectors. This means that the averages <AB>, <AB'>, <A'B> and <A'B'> will all go to zero since they are uncorrelated if Alice and Bob's choices are random and uncorrelated.

jreed wrote:In your so-called correct expression M will always tend to zero. Recall that in EPR experiments, Alice and Bob are free to choose the angles of their detectors. This means that the averages <AB>, <AB'>, <A'B> and <A'B'> will all go to zero since they are uncorrelated if Alice and Bob's choices are random and uncorrelated.

This is complete nonsense, not worthy of any response.

Joy Christian wrote:

jreed wrote:What are you using for the CHSH inequality? Here's an easy explanation of the inequality. Suppose I have two sets of measurements, A, B and A', B'. Then the CHSH inequality is:



Since the measurements must all be +1 or -1 the value of M is always equal to plus or minus 2. This can be easily seen by rewriting M as:



When averaging over a large number of experiments, we obtain M greater than or equal -2 and less than or equal 2. That's all there is to it.

The above argument is fundamentally flawed, as Fred has explained above. The elementary mistake in it is the same mistake that Gill et al. keep making, and it is the same mistake that all Bell devotees keep making. It has been repeatedly explained on these pages, especially by "minkwe." See viewtopic.php?f=6&t=181#p4912.

I have explained the mistake in the above argument in my own way in this paper. See, especially, Eqs. (12) to (26). In essence the seemingly innocent step from the first expression above to the second by "rewriting M" is a cheat. Physically it is nonsense, as I have explained in my paper. All experiments to date have rejected it.

More specifically, the correct expression of M is actually the following:

.

The cheat in the above argument is in surrupticiouly replacing this sum of four separate averages with the following single average:

.

Without this replacement the last step does not follow. But this innocent looking replacement is not justified for the physical experiments, as explained in my paper.

I just finished some simulations to check this out. I used your algorithm with 10,000 trials and wrote two programs. One program calculated CHSH using:



and the other used:



I was careful to initialize the random variables prior to the calculation of each term in the first program, and only initialized it once in the second program. The detector angles were not changed randomly. The spin vector is the only random variable.

The results indicate that the values of CHSH are identical up to random noise, close to 1.4 for each program. Since zeros were not removed, the CHSH values don't violate the inequality CHSH < 2. Either way seems to work so your problem in the posting above is of no concern.

jreed wrote:I just finished some simulations to check this out. I used your algorithm with 10,000 trials and wrote two programs. One program calculated CHSH using:



and the other used:



I was careful to initialize the random variables prior to the calculation of each term in the first program, and only initialized it once in the second program. The detector angles were not changed randomly. The spin vector is the only random variable.

The results indicate that the values of CHSH are identical up to random noise, close to 1.4 for each program. Since zeros were not removed, the CHSH values don't violate the inequality CHSH < 2. Either way seems to work so your problem in the posting above is of no concern.

Garbage in, garbage out.

jreed wrote:I just finished some simulations to check this out. I used your algorithm with 10,000 trials and wrote two programs. One program calculated CHSH using:



and the other used:



I was careful to initialize the random variables prior to the calculation of each term in the first program, and only initialized it once in the second program. The detector angles were not changed randomly. The spin vector is the only random variable.

The results indicate that the values of CHSH are identical up to random noise, close to 1.4 for each program. Since zeros were not removed, the CHSH values don't violate the inequality CHSH < 2. Either way seems to work so your problem in the posting above is of no concern.

Yes, this is what you get. And it's what it should be. According to elementary probability theory, the two expressions are the same, up to random noise. Unfortunately, probability theory seems to be slightly too advanced for both minkwe and Joy Christian to comprehend. But I'm glad that you understand it.

Ignoring the noise generated by Heinera and jreed above, let me get back to the main topic. Such noise is an unfortunate sideeffect of an uncensored forum like this.

It is important to recognize that the upper bound holds for ALL quantum correlations, no mater how complicated the underlying quantum or entangled state is. The physical reason for this has to do with the constant torsion within S^3 as far as the EPR-B correlations are concerned, and more generally with the variable torsion within S^7 for more general or complicated quantum states. As noted in my post above, I have explained this in detail in this paper, as well as on this page of my blog.



PS: One can also see the effect of the torsion within S^3 quite clearly -- and quite directly -- from Eq. (20) of my "Reply to Gill" I have linked above.

Joy Christian wrote:

jreed wrote:I just finished some simulations to check this out. I used your algorithm with 10,000 trials and wrote two programs. One program calculated CHSH using:



and the other used:



I was careful to initialize the random variables prior to the calculation of each term in the first program, and only initialized it once in the second program. The detector angles were not changed randomly. The spin vector is the only random variable.

The results indicate that the values of CHSH are identical up to random noise, close to 1.4 for each program. Since zeros were not removed, the CHSH values don't violate the inequality CHSH < 2. Either way seems to work so your problem in the posting above is of no concern.

Garbage in, garbage out.

"Garbage in, garbage out". Is that the best you can do as a response? Then I must assume that you agree with my statement that it doesn't make any difference which way CHSH is computed. I'm happy to see you understand this.

jreed wrote:"Garbage in, garbage out". Is that the best you can do as a response? Then I must assume that you agree with my statement that it doesn't make any difference which way CHSH is computed. I'm happy to see you understand this.

I think you and Heine have misread what Joy meant. I believe what Joy meant is that in,



The expectation terms are to be taken as independent terms. So that you can't factor like you do in the overall average. IOW, probably better expressed as something like,



It is easy to see from this GAViewer code,

Code: Select all

//Adaptation of Albert Jan Wonnink's original code
//http://challengingbell.blogspot.com/2015/03/numerical-validation-of-vanishing-of.html
function getRandomLambda()
{
   if( rand()>0.5) {return 1;} else {return -1;}
}

function getRandomUnitVector() //uniform random unit vector:
   //http://mathworld.wolfram.com/SpherePointPicking.html
{
   v=randGaussStd()*e1+randGaussStd()*e2+randGaussStd()*e3;
   return normalize(v);
}

   batch test()
{
   set_window_title("Test of Joy Christian's CHSH derivation");
   N=20000; //number of iterations (trials)
   I=e1^e2^e3;
      s=0;
   a1=1.00*e1 +0.01*e2 + 0.01*e3;
   b1=0.707*e1 + 0.707*e2 + 0.01*e3;
      a2=0.01*e1 + 1.00*e2 + 0.01*e3;
   b2=0.707*e1 + -0.707*e2 + 0.01*e3;


      for(nn=0;nn<N;nn=nn+1) //perform the experiment N times
   {
            lambda=getRandomLambda(); //lambda is a fair coin,
                    //resulting in +1 or -1
      mu=lambda * I;  //calculate the lambda dependent mu

            A1=-mu.a1;
            A2=-mu.a2;
            B1=mu.b1;
            B2=mu.b2;
            q=0;
            if(lambda==1) {q=(A1 B1)+(A1 B2)+(A2 B1)-(A2 B2);}
            else {q=(B1 A1)+(B2 A1)+(B1 A2)-(B2 A2);}
            s=s+q;
      }
      mean_F_A_B=s/N;
   print(mean_F_A_B, "f");
      prompt();
}

with a result of mean_F_A_B = 2.828200 + -0.000053*e2^e3 + -0.000022*e3^e1, that the average is being taken across the sum of expectation terms and not individually. But I don't think that was really the issue here.

Ok, let's get back on topic now. And with,



It is possible to get 4. But with,



It is only possible to get as the maximum value. Of course there is a subtle cheat involved to be able to get that. What is it? Let's see if you were paying attention when Michel explained it.

jreed wrote:"Garbage in, garbage out". Is that the best you can do as a response?

That is the only response possible for the nonsense you have been producing here and elsewhere. It is unfortunate that you have repeatedly failed to understand your mistake even after I have explained it to you in several threads. You are putting garbage into your simulations, and as a result getting garbage out. What is more, you have completely missed the point of the current thread, which "Guest" immediately understood: viewtopic.php?f=6&t=199#p5494 (see also the above post by Fred).

PS: See also my response to "minkwe" in the previous thread where I point out the difference between commuting raw scores and non-commuting standard scores in the present context: viewtopic.php?f=6&t=196&start=40#p5426.

The bottom line is that the bound of 2 can be obtained only by cheating. Without cheating the bound is either or , depending on the nature of numbers used.

PPS: My first response to you still stands: viewtopic.php?f=6&t=199#p5506. Physically, the correct derivation of the bound is the one I have presented in this paper.

Joy Christian wrote:PS: See also my response to "minkwe" in the previous thread where I point out the difference between commuting raw scores and non-commuting standard scores in the present context: viewtopic.php?f=6&t=196&start=40#p5426.

Ah, I get it now. A bit of a twist over the usual story about CHSH. I think you could have also asked the question; Why the upper bound on CHSH is 2\/2 and not 2?

FrediFizzx wrote:I think you and Heine have misread what Joy meant. I believe what Joy meant is that in,



The expectation terms are to be taken as independent terms. So that you can't factor like you do in the overall average. IOW, probably better expressed as something like,




with a result of mean_F_A_B = 2.828200 + -0.000053*e2^e3 + -0.000022*e3^e1, that the average is being taken across the sum of expectation terms and not individually. But I don't think that was really the issue here.

Ok, let's get back on topic now. And with,



It is possible to get 4. But with,



It is only possible to get as the maximum value. Of course there is a subtle cheat involved to be able to get that. What is it? Let's see if you were paying attention when Michel explained it.

There is no A3, B3, A4, or B4. In these experiments there are two sets of angles, {a,b} and {a',b'} which the detectors are set to in each experiment and can be switched back and forth. These are picked to maximize CHSH. They are usually chosen as {0, 90}, {45, 135} degrees. The values A, B, A' and B' refer to measurements of the spin with the detectors set at these angles and are either +1 or -1, ordinary numbers. You can think of lights that flash either green (+1) or red (-1). Then CHSH is computed from these spin measurements as:



This is the way I see the experiment and its analysis as taking place.

Leaving aside the above experimentally refuted nonsense by John Reed and getting back to the main topic of this thread, the trivial yet profound physical reason why the upper bound on CHSH is and not has to do with the fact that four mutually orthogonal directions simply cannot exist in three-dimensional space like S^3.

This is easy to verify from the 16 terms expansion of given in my initial post and the following geometric products of the four bivectors representing the four spins:





This of course does not explain why the upper bound is exactly . But as I explained above (and in this paper), that has to do with the torsion within S^3 or S^7.

jreed wrote:There is no A3, B3, A4, or B4. In these experiments there are two sets of angles, {a,b} and {a',b'} which the detectors are set to in each experiment and can be switched back and forth.

You do not understand it, even though this has been explained to death on this forum.

Take a single pair of particles (call it pair #1, with subscript number 1), send one to Alice and another to Bob, so that they can measure at their chosen settings . For this single pair #1, we get


Note that this expression represents 4 incompatible measurements on a single pair of particles (Bob can not measure the same particle at different angles a single measurement can only give us one of those terms! And note that this expression satisfies the inequality since there are only 4 unique numbers in the expression.



This is the argument that is usually extended to averages, to conclude that the averages will also satisfy the inequality. But remember this requires that those averages be calculated on the exact same ensemble of particle pairs, for the argument to be valid.

A foolish physicist/mathematician may think he can simply measure the terms on 4 different pairs and get the same result but, we now have 4 different particle pairs (#1, #2, #3 and #4) each independent from the others



Note that we still have just 4 settings but we now have 8 unique numbers in the expression, not 4 as before, and the inequality does not apply anymore, the argument used to obtain 2 above does not work anymore. A few slightly smarter mathematicians have attempted to argue that all of the above does not matter because statistics will do its magic and everything will cancel out. But we have explained in great detail in the other threads that this is also mistaken. I won't repeat that here, you easily find out if you are interested in further understanding. If the argument does not flow for 4 independent particle pairs, it does not flow for 4 independent ensembles either. You don't eliminate the extra degrees of freedom by measuring on 4 independent ensembles instead of 4 independent particle pairs.

This thread is concerned with explaining what the correct bound should be since we know it isn't 2.