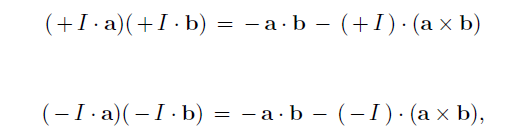From this previous thread; viewtopic.php?f=6&t=183#p4950
Rick Lockyer wrote:Joy is on record stating the cross product averages out over “Nature’s fair coin choice of orientation”. This is categorically incorrect. The math involved for S^3 is the quaternion algebra isomorphic to the bivector subalgebra of GA Joy uses. This is not disputable. The orientation choices for S^3 are a direct byproduct of the two chiral choices for the definition of quaternion algebra.
The two chiral choices for the definition of quaternion algebra come about in the products of non-scalar basis elements. Define the scalar quaternion basis element as e_0 == 1, and an ordered triplet of the non-scalar basis elements e_1, e_2, and e_3 basis elements as
(e_1 , e_2, e_3 ) == (e_2 , e_3, e_1 ) == (e_3 , e_1, e_2 )
These equivalent forms imply the following quaternion basis element product rules cyclic left to right for positive signed outcomes and cyclic right to left for negative signed outcomes:
e_1 * e_2 = e_3
e_2 * e_3 = e_1
e_3 * e_1 = e_2
e_1* e_3 = -e_2
e_2 * e_1 = -e_3
e_3 * e_2 = -e_1
If we assign x:1, y:2 and z:3 significance to the indexes, we have just defined a right handed chiral system, absolutely relevant to S^3 orientation. The opposite orientation would be described by a different basis set which I will call f_x, with the following ordered triplet with identical xyz index significance:
(f_1, f_3, f_2) == (f_3, f_2, f_1) == (f_2, f_1, f_3)
The rule of algebraic element addition for any algebra over the field of real numbers as we have here is the following for real coefficients A_j and B_j:
A = A_j e_j sum over j for the dimension of the algebra in question
B = B_j e_j sum over j for the dimension of the algebra in question
A + B = (A_j + B_j) e_j sum over j for the dimension of the algebra in question
The extremely important thing to take away from this non-disputable rule of algebraic element addition, which is very relevant to our discussion, is that coefficients attached to IDENTICAL basis elements add in the final result. Therefore, if we have A represented in a right handed quaternion system, and B represented in a left handed quaternion system, we have
A + B =
A_0 e_0 + A_1 e_1 + A_2 e_2 + A_3 e_3 +
B_0 f_0 + B_1 f_1 + B_2 f_2 + B_3 f_3
If we wish to simplify this expression, we must find a way to map either e_j to f_j or f_j to e_j such that the coefficients for A and B are now attached to a consistent set of basis elements such that we may combine their coefficients. There is such a map, it is:
e_0 -> f_0
e_k -> -f_k for k = 1 to 3
With this map or the converse, we have
A + B = (A_0 + B_0) e_0 == (A_0 + B_0) f_0 since e_0 == f_0
So we have indeed dispatched the non-scalar portion. But this is NOT what Joy is doing. A and B are PRODUCTS, which complicates things a bit. Let a and b be right handed algebraic elements, and a’ and b’ be left handed algebraic element representations using the same coefficients as a and b. We then have four possible combinations of handedness products: C = a*b, D = a*b’, E = a’*b and F = a’*b’. Once again, to make any kind of correspondence between C, D, E and F we must first map each expression to a SINGULAR basis set. Trust me when I say it does not matter if we map e to f or f to e, the cross product cannot be removed by any combination of chiral forms. If you do not trust me, well do the damn math for yourself! I am going to map f to e for C, D, E, and F.
C =
+ (a_0 b_0) e_0*e_0 + (a_1 b_1) e_1*e_1 + (a_2 b_2) e_2*e_2 + (a_3 b_3) e_3*e_3
+ (a_0 b_1) e_0*e_1 + (a_1 b_0) e_1*e_0 + (a_2 b_3) e_2*e_3 + ( a_3 b_2) e_3*e_2
+ (a_0 b_2) e_0*e_2 + (a_2 b_0) e_2*e_0 + (a_3 b_1) e_3*e_1 + (a_1 b_3) e_1*e_3
+ (a_0 b_3) e_0*e_3 + (a_3 b_0) e_3*e_0 + (a_1 b_3) e_1*e_3 + (a_3 b_1) e_3*e_1
=
+ (a_0 b_0 – a_1 b_1 – a_2 b_2 – a_3 b_3) e_0
+ (a_0 b_1 + a_1 b_0 + a_2 b_3 – a_3 b_2) e_1
+ (a_0 b_2 + a_2 b_0 + a_3 b_1 – a_1 b_3) e_2
+ (a_0 b_3 + a_3 b_0 + a_1 b_2 – a_2 b_1) e_3
D =
+ (a_0 b_0) e_0*f_0 + (a_1 b_1) e_1*f_1 + (a_2 b_2) e_2*f_2 + (a_3 b_3) e_3*f_3
+ (a_0 b_1) e_0*f_1 + (a_1 b_0) e_1*f_0 + (a_2 b_3) e_2*f_3 + ( a_3 b_2) e_3*f_2
+ (a_0 b_2) e_0*f_2 + (a_2 b_0) e_2*f_0 + (a_3 b_1) e_3*f_1 + (a_1 b_3) e_1*f_3
+ (a_0 b_3) e_0*f_3 + (a_3 b_0) e_3*f_0 + (a_1 b_3) e_1*f_3 + (a_3 b_1) e_3*f_1
=
+ (a_0 b_0 + a_1 b_1 + a_2 b_2 + a_3 b_3) e_0
+ (– a_0 b_1 + a_1 b_0 – a_2 b_3 + a_3 b_2) e_1
+ (– a_0 b_2 + a_2 b_0 – a_3 b_1 + a_1 b_3) e_2
+ (– a_0 b_3 + a_3 b_0 – a_1 b_2 + a_2 b_1) e_3
E =
+ (a_0 b_0) f_0*e_0 + (a_1 b_1) f_1*e_1 + (a_2 b_2) f_2*e_2 + (a_3 b_3) f_3*e_3
+ (a_0 b_1) f_0*e_1 + (a_1 b_0) f_1*e_0 + (a_2 b_3) f_2*e_3 + ( a_3 b_2) f_3*e_2
+ (a_0 b_2) f_0*e_2 + (a_2 b_0) f_2*e_0 + (a_3 b_1) f_3*e_1 + (a_1 b_3) f_1*e_3
+ (a_0 b_3) f_0*e_3 + (a_3 b_0) f_3*e_0 + (a_1 b_3) f_1*e_3 + (a_3 b_1) f_3*e_1
=
+ (a_0 b_0 + a_1 b_1 + a_2 b_2 + a_3 b_3) e_0
+ (a_0 b_1 – a_1 b_0 – a_2 b_3 + a_3 b_2) e_1
+ (a_0 b_2 – a_2 b_0 – a_3 b_1 + a_1 b_3) e_2
+ (a_0 b_3 – a_3 b_0 – a_1 b_2 + a_2 b_1) e_3
F =
+ (a_0 b_0) f_0*f_0 + (a_1 b_1) f_1*f_1 + (a_2 b_2) f_2*f_2 + (a_3 b_3) f_3*f_3
+ (a_0 b_1) f_0*f_1 + (a_1 b_0) f_1*f_0 + (a_2 b_3) f_2*f_3 + ( a_3 b_2) f_3*f_2
+ (a_0 b_2) f_0*f_2 + (a_2 b_0) f_2*f_0 + (a_3 b_1) f_3*f_1 + (a_1 b_3) f_1*f_3
+ (a_0 b_3) f_0*f_3 + (a_3 b_0) f_3*f_0 + (a_1 b_3) f_1*f_3 + (a_3 b_1) f_3*f_1
=
+ (a_0 b_0 – a_1 b_1 – a_2 b_2 – a_3 b_3) e_0
+ (– a_0 b_1 – a_1 b_0 + a_2 b_3 – a_3 b_2) e_1
+ (– a_0 b_2 – a_2 b_0 + a_3 b_1 – a_1 b_3) e_2
+ (– a_0 b_3 – a_3 b_0 + a_1 b_2 – a_2 b_1) e_3
Joy starts with pure bivector values, meaning we have A_0 = B_0 = 0. This does simplify things a bit. Substituting we have
C =
– (a_1 b_1 + a_2 b_2 + a_3 b_3) e_0
+ (a_2 b_3 – a_3 b_2) e_1
+ (a_3 b_1 – a_1 b_3) e_2
+ (a_1 b_2 – a_2 b_1) e_3
D =
+ (a_1 b_1 + a_2 b_2 + a_3 b_3) e_0
– (a_2 b_3 – a_3 b_2) e_1
– (a_3 b_1 – a_1 b_3) e_2
– (a_1 b_2 – a_2 b_1) e_3
E =
+ (a_1 b_1 + a_2 b_2 + a_3 b_3) e_0
– (a_2 b_3 – a_3 b_2) e_1
– (a_3 b_1 – a_1 b_3) e_2
– (a_1 b_2 – a_2 b_1) e_3
F =
– (a_1 b_1 + a_2 b_2 + a_3 b_3) e_0
+ (a_2 b_3 – a_3 b_2) e_1
+ (a_3 b_1 – a_1 b_3) e_2
+ (a_1 b_2 – a_2 b_1) e_3
So with pure bivectors (quaternions) we have C = –D = –E = F. Since these are the ONLY chiral combinations available, there is absolutely no way to clear the non-scalar component of a sum of similar products of pure bivectors through any possible modification of orientation for individual products.
So we took Lockyer's advice and did the math for ourself. For the following analysis, only C and F above really matter as we would never have mixed left-right handed pairs since the particle pairs themselves form the left or right handed system. What Lockyer's error is that when he calculated F (left handed) the first time, he double translated it. IOW, he did the mapping twice. And you might notice that the LHS of the equations for C and F have typos in them ((a_3 b_1) f_3*f_1 and (a_1 b_3) f_1*f_3 appear twice each) but it is corrected in the RHS. I have underlined them above in the quote. Anyways... back to the double mapping. As can be seen by the multiplication tables here,
http://captaincomputersensor.net/quaternions.html ,
the mapping Lockyer specified above is already contained in the difference between the two tables. So when he was calculating F, he did the left handed multiplication and then applied the mapping again by applying the minus signs to the appropriate elements. Of course that will take you right back to the beginning of what you were doing and no translation occured at all. We can see what he did by taking the element (a_2 b_3) f_2*f_3 then looking up f_2*f_3 in the left handed table equals -e_1 so the result should just be -a_2 b_3 for the e_1 line but you can see that he had it as +a_2 b_3 in the RHS in the e_1 line so he multiplied again by -1.
When only mapped once and dispensing with the zero components we get for F,
F =
– (a_1 b_1 + a_2 b_2 + a_3 b_3) e_0
+ (-a_2 b_3 + a_3 b_2) e_1
+ (-a_3 b_1 + a_1 b_3) e_2
+ (-a_1 b_2 + a_2 b_1) e_3
And we can see that C is no longer equal to F as it should be since common sense logic dictates that if you start with the same formulas for left and right that upon translation of one of them, they should no longer be equal. Now... from what we learned about this from using GAViewer, we can check this simply by reversing the order of the multipication. And again dispensing with the zero components we have,
F = (b1 e1 + b2 e2 + b3 e3)(a1 e1 + a2 e2 + a3 e3)
=
+a1b1 e1e1 + a2b2 e2e2 + a3b3 e3e3
+a2b3 e3e2 + a3b2 e2e3
+a3b1 e1e3 + a1b3 e3e1
+a1b2 e2e1 + a2b1 e1e2
=
-(a1b1 + a2b2 + a3b3)e0
+(-a2b3 + a3b2)e1
+(-a3b1 + a1b3)e2
+(-a1b2 + a2b1)e3
Check complete and they match. Now when we add C to F and divide by two to get the average we obtain,
(C + F)/2 = -(a1b1 + a2b2 + a3b3) + 0 = -a.b
As expected. QED. So we have proven that Joy's model is correct a little different way.