SciPhysicsForums.com

Hello to all:

I have been quietly working on my Lorentz Force paper, for which I last posted a draft on March 5 at https://jayryablon.files.wordpress.com/ ... -2-spf.pdf. Much of my effort has been to perfect sections 14 and 16. It turns out that to do this right in view of quantum uncertainties when two charges get very close together is a substantial challenge.

In the course of this undertaking, just last night I realized that the key is in fact energy - time uncertainty. From a viewpoint first espoused by Pauli, it has long been held that there is no energy - time complementarity a) because energy is lower-bounded and b) because time is a scalar parameter not an operator. But the geodesic description of the Lorentz force make the electromagnetic interaction a consequence of varying rates of time flow in relation to proper time flow, . This means that time in this situation isn't just a parameter: in any physical system, every electron and every quark and ever other particle has its own uique that is a function of its motion, its mass and charge, the EM field in which it sits, and the gravitational field in which it sits, see, e.g., (11.14) through (11.16) of https://jayryablon.files.wordpress.com/ ... -2-spf.pdf.

So when we get down to the level of individual quantum particles, the electromagnetic interaction energy has a statistical variation from one particle to the next, which is connected to also having a statistical variation from one particle to the next, such that a wider spread in energy complements a narrower spread in 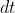and leads to energy-time complementarity of the form . The energy is, however, the electromagnetic interaction energy which does not have a lower bound because EM interactions can both attract and repel, and the time t is not the parameter measured by an observer but the time t associated with the of the specific particle in question. 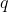And again, the association of a distinct with each charge with mass 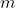is a direct and immediate consequence of deducing the Lorentz force from a minimized variation of the metric interval, .

I will write this all up and get a clean draft posted (with a fair amount of development since last time) as soon as I can.

Jay

Jay, please define what dt/dtau for a particle actually means in an operational sense. A simple example. Also. I'm mystified by the claim of a natural energy-time complementarity stemming from motion.....gravitational potential. On my interpretation, those two relativistic factors have the property that the greater the spread in KE or grav potential, also a greater spread in dt (necessarily referred to some fixed reference frame/potential), not the inverse. But you evidently have in mind a different meaning to what 'spread' means in this context.

Q-reeus wrote:Jay, please define what dt/dtau for a particle actually means in an operational sense. A simple example. Also. I'm mystified by the claim of a natural energy-time complementarity stemming from motion.....gravitational potential. On my interpretation, those two relativistic factors have the property that the greater the spread in KE or grav potential, also a greater spread in dt (necessarily referred to some fixed reference frame/potential), not the inverse. But you evidently have in mind a different meaning to what 'spread' means in this context.

Hi Q-reeus:

I have uploaded my current draft to https://jayryablon.files.wordpress.com/ ... -8-spf.pdf, because it contains enough new matter since March that it would not be possible to answer your questions using the March 5 draft. Equation numbers below will reference this later draft. Now, briefly:

In an operational sense, if I am an observer using an uncharged, neutral oscillator (clock) to keep time, and there is another oscillator at rest nearby in flat spacetime which is the same in all respects as the first oscillator except it has a net electric charge, then the two oscillators will have different flow rates of time. See (11.21) and (11.22). It is (11.21) which show how this leads to what really is physically observed for EM potential energies.

Next, I am not claiming complementary from motion or gravitational potential (though I will keep an eye out for that). Only for EM interactions. The two key equations to start with are (11.23) and (14.17). Note that (14.17) is corrected in relation to what I had on March 5 that had an error in calculation. What is key is that (at rest in flat spacetime) in (11.23) but in (14.17) which is inversely proportional as regards .

It was at (15.18) when I started looking at the numerical values of the statistical spreads in the potential energy that I realized Thursday night that this needs to go hand in hand with a statistical spread in the rate, and leads to energy - time complementary. That will be the direction in which my writeup will now go. Stay tuned.

Best regards,

Jay

Hi Jay

I have folllowed a couple of Susskind's online courses this last few months: "Basic Concepts" (which turned out to be an introduction to QFT) and am now working through SUSY. About 20 hours per course.

In lecture 10 of QFT, he says that" integrating over time conserves energy" and "integrating over space conserves momentum" wrt Feynman diagram values. Is this relevant to your note about energy-time complementarity? You note that you have equations for the QED effect but not yet for gravitation or motion. I think QED is easier than QCD wrt re-normalisation because of the small coupling constant. In QFT there is, apparently, no single correct answer as the particles get closer together without limit. You pick a small cut-off delta minimum distance separation and try to engineer a non-infinite answer for the Feynman diagram value for that particular cut-off. Are you doing the same sort of thing in your equations, i.e. allowing for the answers to be different for different separations?

Apologies if this does not make much sense!

Jay!

I am so heartened to see Einstein's program going forward step by hard-fought step. This key idea (varying rates of time flow) promises to seal the game. Looking forward to reading the paper.

All best,

Tom

Wasn't Weyl's gauge theory a variable time theory that AE rejected because he argued that it implied that a particle's mass depended on its history?

Yablon wrote:Hi Q-reeus:

I have uploaded my current draft to https://jayryablon.files.wordpress.com/ ... -8-spf.pdf, because it contains enough new matter since March that it would not be possible to answer your questions using the March 5 draft. Equation numbers below will reference this later draft. Now, briefly:

In an operational sense, if I am an observer using an uncharged, neutral oscillator (clock) to keep time, and there is another oscillator at rest nearby in flat spacetime which is the same in all respects as the first oscillator except it has a net electric charge, then the two oscillators will have different flow rates of time. See (11.21) and (11.22). It is (11.21) which show how this leads to what really is physically observed for EM potential energies.

Next, I am not claiming complementary from motion or gravitational potential (though I will keep an eye out for that). Only for EM interactions. The two key equations to start with are (11.23) and (14.17). Note that (14.17) is corrected in relation to what I had on March 5 that had an error in calculation. What is key is that (at rest in flat spacetime) in (11.23) but in (14.17) which is inversely proportional as regards .

It was at (15.18) when I started looking at the numerical values of the statistical spreads in the potential energy that I realized Thursday night that this needs to go hand in hand with a statistical spread in the rate, and leads to energy - time complementary. That will be the direction in which my writeup will now go. Stay tuned.

Best regards,

Jay

Jay, sorry about delay my part and thanks for responding and clarifying. Your idea sort of rang a bell. Many years ago I had the notion there might be an electrodynamic analogue to Mach's principle. Charge up a Faraday cage to a high potential, and all charges within would have altered inertia - opposite signs for opposite charges. But then it occurred to me that nature provides such a scenario - large thunderstorm clouds with massive +ve and -ve separated charge regions. And there is no evidence of any runaway processes (-ve inertia!) that easy sums show would be the case if any such Mach's principle analogue were naively correct. Later, I came across an article by L.Brillouin where he mentioned just such attempts to determine if static charge ptential can effect electrodynamic inertia - and that there was no such observed effects. So I just did a quick search and found the following article: http://www.mdpi.com/2227-7390/3/2/190/pdf

Brillouin's observations are mentioned first part, p199 there and may or may not have direct relevance to your theory. I could understand a rather trivial reason for changed oscillator frequency if charged up - electrostaic stiffening of oscillator overall spring constant (think of arms of an electroscope flying apart). But I doubt that's what you have in mind.

Kevin

Q-reeus wrote:Jay, sorry about delay my part and thanks for responding and clarifying. Your idea sort of rang a bell. Many years ago I had the notion there might be an electrodynamic analogue to Mach's principle. Charge up a Faraday cage to a high potential, and all charges within would have altered inertia - opposite signs for opposite charges. But then it occurred to me that nature provides such a scenario - large thunderstorm clouds with massive +ve and -ve separated charge regions. And there is no evidence of any runaway processes (-ve inertia!) that easy sums show would be the case if any such Mach's principle analogue were naively correct. Later, I came across an article by L.Brillouin where he mentioned just such attempts to determine if static charge ptential can effect electrodynamic inertia - and that there was no such observed effects. So I just did a quick search and found the following article: http://www.mdpi.com/2227-7390/3/2/190/pdf

Brillouin's observations are mentioned first part, p199 there and may or may not have direct relevance to your theory. I could understand a rather trivial reason for changed oscillator frequency if charged up - electrostaic stiffening of oscillator overall spring constant (think of arms of an electroscope flying apart). But I doubt that's what you have in mind.Kevin

Hi Kevin,

We must be communicating telepathically or something, because just yesterday I was thinking about how I am about the write up that two repelling electrons can, on average, as a material limit of nature, get no closer to one another than the classical electron charge radius which is about as large as a typical nuclear radius. See my section 12 and partially complete section 15 at https://jayryablon.files.wordpress.com/ ... -8-spf.pdf. And I was asking myself whether there might be some observed physical phenomenon that manifests what happens when too many charges all of the same sign are accumulated too closely together that nature does not like it. And, no pun intended, I was struck by lightening perhaps being a very primordial example of nature spontaneously saying "these charges are closer together than I can allow them to be -- so --- booom!"

I have also had in mind that the time dilation or contraction as between two oscillators of different charges at equipotential might be explained in terms of changes to the physical characteristics of the oscillator / clock, e.g., spring tension and the like. This is just like how in special relativity one might say that the time dilation happens because the moving clock gets more massive relative to the stationary clock and as a result the time being kept appears to dilate. Then we are left with a chicken and egg: does the time only appear to dilate because the mechanics of the moving clock are altered? Sort of like pre-1905 after Lorentz had his transformation but before Einstein made it a fundamental measurement finding. Or, does the time actually dilate and thus alter the mechanics of the moving clock? Which is how Einstein advanced Lorentz. The latter explanation is of course the accepted one, because SR is at bottom a theory of how we measure time and length and mass -- geometrodynamics. The general theory then said that if your geometry is curved as well, you will also measure time differently at different places in the geometry and this curvature will be directly connected to gravitation. But here too, there is an explanation in terms of the mechanics of the clocks at different places in the gravitational field, but it is a consequence of how we measure and what the physics does to our measurements.

So, I can easily see EM time dilations messing with the mechanics of a clock or the vice versa view. But at bottom, from a geometrodynamic view, if all of physics is about how and what we measure and our role as curious inquiring scientists is to figure out exactly how this is so, then we must regard the time dilation (for attraction) or contraction (for repulsion) as rock bottom fundamental, and whatever else happens to the clocks to be a consequence of this change in the rate of flow of time.

In many ways, the whole point of my paper is that the Lorentz force itself is direct and powerful evidence that all of electrodynamics can also be explained by how rates of time flow change for different charges in an EM field. If we deduce the Lorentz force from a minimized variation (section 6) just as we do the gravitational geodesic equation, then the only way to properly interpret that result in view of everything else we know about and expect from field theory is to have different charges associated with different rates of time flow (section 8). The whole rest of my paper is a) showing further consequences of this and b) showing that these further consequences do not run afoul of anything else we know to be true about the natural world

Jay

poor boy wrote:Wasn't Weyl's gauge theory a variable time theory that AE rejected because he argued that it implied that a particle's mass depended on its history?

The main objection I am aware of that Einstein and others had to gauge theory when it really used a "gauge" and not a "phase" transformation, is the resizing of electrons that simply is not observed. I review this directly, in section 22 of https://jayryablon.files.wordpress.com/ ... -8-spf.pdf.

Jay

thray wrote:Jay!

I am so heartened to see Einstein's program going forward step by hard-fought step. This key idea (varying rates of time flow) promises to seal the game. Looking forward to reading the paper.

All best,

Tom

Thanks Tom, I appreciate your feedback, and yes, after 110+ years, it is time for everyone to get out of the habit of thinking about time flow as a monotonic phenomenon. Just like we use statistical averaging and specify standard deviations for any phenomenon that involves the composite behavior of a large number of elements (generally, particles) as we have at least since the time of Boltzmann, we must now start to think and talk about the "average" rate at which time flows for a large ensemble of particles as well as the standard deviations in the time flow rate as among individual particles in the ensemble. Once we do that, time uncertainty (really, standard deviation for time flow) not only has a genuine physical meaning because time flow is no longer a monotone (as we should have learned from AE in 1905), but there is no escaping a statistical view of time flow along with all the usual statistical averaging and deviation methods. Then, of course, we expect that this has to be complementary to an equally-statistical energy spread . The only question becomes, because we need to remove any lower bound, what is the physical nature of the energy uncertainty that is complementary to the time uncertainty? The EM interaction energy is a perfect fit, precisely because EM admits both attraction and repulsion, and therefore both positive and negative energies of interaction.

Wolfgang Pauli, the resident grump of his generation of physicists, set out the reasons why energy-time uncertainty could not exist along with momentum-position uncertainty, because a) energy needed to have a lower bound (good reason, tied to Feynman–Stueckelberg and Dirac electron theory) and b) time was a monotonic parameter (bad reason, did not learn all that should be learned from AE). Not only has that left a huge gaping question as to why nature would exhibit spacetime and energy-momentum unity everywhere but in the Heisenberg relations, but it also precluded the much-more-sane view of uncertainty that Niels Bohr tried to take, that all this uncertainty business was simply much ado about Fourier Transforms. Once we can establish energy-time uncertainty, than all this uncertainly business including philosophical debates about determinism and free will and predictability and God playing dice or not really does become a lot of hyper-kinetic buzzing about what is at bottom, the Fourier Transforms and momentum space harmonics that sit at the root of virtually every electronic signalling device ever made, and statistical methods that were used in the late 1800s for thermodynamics before Planck ever said a word about quantization or Heisenberg about uncertainty, without anybody ever getting too exercised.

Jay

Ben6993 wrote:Hi Jay

I have folllowed a couple of Susskind's online courses this last few months: "Basic Concepts" (which turned out to be an introduction to QFT) and am now working through SUSY. About 20 hours per course.

In lecture 10 of QFT, he says that" integrating over time conserves energy" and "integrating over space conserves momentum" wrt Feynman diagram values. Is this relevant to your note about energy-time complementarity? You note that you have equations for the QED effect but not yet for gravitation or motion. I think QED is easier than QCD wrt re-normalisation because of the small coupling constant. In QFT there is, apparently, no single correct answer as the particles get closer together without limit. You pick a small cut-off delta minimum distance separation and try to engineer a non-infinite answer for the Feynman diagram value for that particular cut-off. Are you doing the same sort of thing in your equations, i.e. allowing for the answers to be different for different separations?

Apologies if this does not make much sense!

Hi Ben, Long time no talk.

Noether's theorem, which is highly profound both philosophically and operationally, says that each symmetry of nature is connected to a conservation law. Invariance under time displacement implies energy conservation. Invariance under position displacement implies momentum conservation. Lorentz symmetry implies angular momentum conservation. And gauge invariance implies conserved electric charge. The philosophical beauty is that every time we discover a new symmetry which is a theoretical visualization of something that does not change under some operation, we have discovered (or validated) a physical conservation law. The operational beauty say that if we want to discover (or newly-validate) conserved physical entities, we need to find new symmetries. So now, to your query.

I am not a fan of SUSY, but let's not go there. Energy is conserved on a statistical basis, because due to uncertainty and Planck's constant not being equal to zero, for a very teensy-weensy period of time (that is a technical term that one cannot comprehend without at least four years in graduate school ) we can actually have the energy not be conserved. But after more than this teensy amount of time, i.e., after we integrate over some time that is not so tiny, this violation of energy conservation becomes rectified and the energy is conserved. Same with space and momentum. So when Susskind says "integrating over time conserves energy" and "integrating over space conserves momentum," you will see that he is tying together the symmetry and the conserved quantity aspects of Noether's theorem. Specifically, in the quantum world, when we are looking at very, very small periods of time and regions of space, there are very violent quantum fluctuations. cf. the quantum vacuum where our good friend Fred Diether lives. So moving forward by, say, seconds, or moving over by, say, meters which are not too much larger than the Planck time and length, nature is not symmetric under time or space translation, because what I observe a tiny part of a second later or a tiny part of a meter over is not the same as what I observed initially. And, no symmetry means no conservation. But then when I go to a "wide angle" view and do not see the granularity at the Planck scale, the world looks the same at all times and at all places, so there is now a symmetry, so by Noether, energy and momentum are conserved. That is, a "wide angle" -- the "view from 30,000 feet" -- is just another way of saying that I am "integrating" over the larger regions of time and space, so I recover the conservation laws.

This is the same sort of thing I am presently dealing with as I dive into energy - time uncertainty. However, these cutoffs you refer to are a plague that come along with renormalization, and it would be very desirable to reach the same results but with a different process to get there.

Also, when you say "you note that you have equations for the QED effect but not yet for gravitation or motion," I want to be clear. I am not looking to find this. If it is there, it will find me. If I can pass along to others one of the most important lessons I have learned over my years of trying to find out new things about the natural world, it is this: It is so very important to get rid of one's preconceptions about what one ought to find and how the world ought to be. You have to objectively follow the equations wherever they take you and interpret whatever they are saying to you. Dirac perhaps said it best, when he once said that his Dirac "equation is more intelligent than its author." Those of us who try to find new things about the natural universe do not talk to our equations. Our equations talk to us.

Jay

PS: The last statement is why I am not a fan of SUSY: its authors are talking to its equations rather than vice versa, because they have preconceived that particle types at any given spin ought to have counterparts at other spins.

Hi Jay

Thank you very much for the excellent explanation. Nice to see a good overview by a kindly expert!

I have met before what you have said, in your first two paragraphs, in my readings about particle physics and in the 100+ hours of Susskind's online lectures, though I could not have tied it all together like you have.

My main reason for writing previously was to find out if you were aiming at a single right answer or were aiming at a range of answers depending on the degree of separation of particles. And as you said: " However, these cutoffs you refer to are a plague that come along with renormalization, and it would be very desirable to reach the same results but with a different process to get there" then I think you are expecting different 'results' for different cutoffs. However you also said to Q-reeus: "two repelling electrons can, on average, as a material limit of nature, get no closer to one another than the classical electron charge radius which is about as large as a typical nuclear radius". [I have here just stopped to read your Section 15 which is very interesting and readable, though I need to revisit it!] It is possible that the electrons would collapse/disintegrate if somehow [in some weird type of star etc] forced to a smaller separation, especially easy for me to believe as I think electrons are composed of preons.

So it maybe that electrons have separation size restraints and in general I am accepting the idea of different cut-offs for different purposes to avoid infinities. I am trying to see it as a fact of nature rather than as a flaw to be overcome. My analogy is with the length of a coastline. [There was also a related Horizon program about 'how long is a piece of string'.] The length of a coastline is inversely proportional to the length of your ruler. With a small enough ruler the length of the coastline can aproach infinity. But we are born into a world where our rulers are of a medium size. Not too small and not too large. But you need to decide the length of your ruler before making the measurement and to realise the the answer depends on the particular ruler used.

I previously studied, in 2015, the first seven of the ten Susskind SUSY lectures. I gave up after seven lectures as I did not believe that fermions and bosons were paired as unique partners. My belief is influenced by preons of course and I see fermions and bosons as different combinations of the same preon building blocks. So in a preon model, the fermions and bosons are clearly related via preons. Without using preons, and where the fermions and bosons are mysterious point entities, it seems to me that SUSY is a way to try to link fermions to bosons. Susskind kept apologising for the oddness of the idea of an operator that turned a fermion into a boson and vice versa. But in my preon model, that operator seems quite reasonable. You combine a fermion with a fermion and get a boson by aggregating the preons and see what you get. I have returned to the course, however, because my preon model may fit a 3-3-1 model {e.g. Le Tho Hue, Le Duc Ninh (October 2015) “The simplest 3-3-1 model”. arXiv:1510.00302 [hep-ph]} which is a SUSY model ... so I need to finish the SUSY course. Ninh's paper predicts one particle with electric charge 0.5 and another with charge = 1/6. These happen to be the charges on each preon and sub-preon, repectively, in my model, which is why the 3-3-1 may be important for me.

I am also following an online course on group theory and have an abstract text book for SU(2) and SU(3). I also studied ring and group theory at university in the late 60s and should look up my notes! Though I am sure they did not go far enough. You might notice that I keep finding study material to prevent me from getting to grips with GR ...

Also the SUSY course uses Grassmann numbers, which I have read somewhere are the non-quantised version of Clifford Algebra variables. Where you can have non-zero square roots of zero, and where odd numbers anticommute and even numbers commute. More reading required ...

Jay,

Thanks for the stimulating dialogue.

If time flows with frequency, frequency in-phase and out-of-phase destructive and constructive effects statistically define moments between 0 (destructive) and 1 (constructive). So in the open interval (0,1) there is a continuous exchange of moments of destructive-constructive action as varieties of frequencies compete. It seems to me that you want to average constructive-destructive frequencies on the closed interval [0,1] to a single number in an arbitrary moment of time. This would seem to me to define time out of existence, as it separates time from Minkowski spacetime.

A continuous flow on the half open interval [0,1) integrates time with space. Perelman’s proof of 3-sphere simple connectedness explains, by application of Ricci flow with surgery, the continuous direction of time away from singularity, and its beginning on a new interval [0,1). Now, that doesn’t make the Poincaré conjecture necessarily physical; however, Ricci flow being so intimately connected with heat flow suggests that it’s worth looking into. It also meets your criterion: “The EM interaction energy is a perfect fit, precisely because EM admits both attraction and repulsion, and therefore both positive and negative energies of interaction.”

I’m still trying to digest your paper, so I haven’t reached any conclusions. Just thinking out loud.

Best,

Tom

poor boy wrote:Wasn't Weyl's gauge theory a variable time theory that AE rejected because he argued that it implied that a particle's mass depended on its history?

This paper, [http://www.math.toronto.edu/~colliand/426_03/Papers03/C_Quigley.pdf], has some valuable insight on the development of gauge theory.

Weyl was a committed Liebnizian, so it isn't surprising he would seek an infinitesimal solution. Where this differs from Einstein is in indistinguishability of past and future events ('all physics is local'.)

"Weyl probably wished he had not sent his paper to Einstein to be published, since Einstein included this negation as a postscript. He, nonethe- less, admired Weyl as a brilliant mathematician, and was greatly impressed by his novel geometric ideas. Weyl, on the other hand, was not convinced and continued to develop his true infinitesimal geometry. He thought,

'It would be remarkable if in Nature there was realized instead an illogical quasi-infinitesimal geometry, with an electromagnetic field attached to it.'

"Weyl’s gauge theory was paid little heed during the next decade. With the coming of the Quantum era, attention moved to the microscopic regime."

Tom

thray wrote:This paper, http://www.math.toronto.edu/~colliand/4 ... uigley.pdf, has some valuable insight on the development of gauge theory.

Tom, thanks, that is a nice little article. This is essentially the same thing I am reviewing, from my own view of the subject, in section 22 of https://jayryablon.files.wordpress.com/ ... -8-spf.pdf which I know you are presently reading.

Jay

HEY Jay

Thank you very much for the excellent explanation. Nice to see a good overview by a kindly expert!

Dear friends:

I have uploaded the latest draft of my paper to https://jayryablon.files.wordpress.com/ ... cs-8-4.pdf.

Since I posted the last draft on April 16, I have done some substantial revamping of sections 11 through 15, which are contained in sections 11 through 14 of the present document. If you have reviewed the previous draft, then to save you some time I suggest the following:

Start reading from equation (11.23) on page 55, through the end of section 11 on page 59. Here is were I preview a lot of the material I will be adding in the coming days.

Then, skip most of section 12, and start at after (12.18) to see the new material added to that section.

From there, sections 13 and 14 of this new draft are entirely new, and replace much of what were sections 13 to 15 in the April 16 draft. I will be adding more in the upcoming days, but this draft is a good representation of where I am headed at present.

As always, I am happy to respond to queries, critiques, idle banter, and anything else you may want to throw my way.

Jay