ROTFLMAO! Schmelzer has promoted their mathematical nonsense to a locked thread like it is something special.
Schmelzer's and Gill's mathematical nonsense
70 posts
• Page 1 of 4 • 1, 2, 3, 4
Schmelzer's and Gill's mathematical nonsense
http://ilja-schmelzer.de/forum/showthread.php?tid=58
ROTFLMAO! Schmelzer has promoted their mathematical nonsense to a locked thread like it is something special. Well, that is their problem as all the world can see that they for some unknown reasons are having extreme difficulty with some pretty simple math and physics postulates. It can't be ignorance because it has been explained to them exactly what they are doing wrong many times. And I can't believe it is pure stupidity so the only conclusion left is pure dishonesty. If anyone here would like us to explain once again why they are totally wrong, please post your questions.
Well, that is their problem as all the world can see that they for some unknown reasons are having extreme difficulty with some pretty simple math and physics postulates. It can't be ignorance because it has been explained to them exactly what they are doing wrong many times. And I can't believe it is pure stupidity so the only conclusion left is pure dishonesty. If anyone here would like us to explain once again why they are totally wrong, please post your questions.
ROTFLMAO! Schmelzer has promoted their mathematical nonsense to a locked thread like it is something special.
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Schmelzer's and Gill's mathematical nonsense
FrediFizzx wrote:http://ilja-schmelzer.de/forum/showthread.php?tid=58
ROTFLMAO! Schmelzer has promoted their mathematical nonsense to a locked thread like it is something special.Well, that is their problem as all the world can see that they for some unknown reasons are having extreme difficulty with some pretty simple math and physics postulates. It can't be ignorance because it has been explained to them exactly what they are doing wrong many times. And I can't believe it is pure stupidity so the only conclusion left is pure dishonesty. If anyone here would like us to explain once again why they are totally wrong, please post your questions.
It is not worth paying any attention to their incompetence and/or dishonesty, but for what it's worth I have already dispelled their confusion at the following thread:
viewtopic.php?f=6&t=222&start=20#p6569
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Schmelzer's and Gill's mathematical nonsense
***
For the record, here are some examples of how several independent authors have repeatedly exposed Richard Gill's embarrassing mathematical mistakes:
1) https://pubpeer.com/publications/D985B4 ... 22#fb27706
2) https://pubpeer.com/publications/4C65BF ... 273C68E70E
3) https://www.researchgate.net/publicatio ... al_Reality
4) http://arxiv.org/abs/1501.03393
5) http://arxiv.org/abs/1203.2529
6) viewtopic.php?f=6&t=49&p=2545&hilit=third+rate#p2545
***
For the record, here are some examples of how several independent authors have repeatedly exposed Richard Gill's embarrassing mathematical mistakes:
1) https://pubpeer.com/publications/D985B4 ... 22#fb27706
2) https://pubpeer.com/publications/4C65BF ... 273C68E70E
3) https://www.researchgate.net/publicatio ... al_Reality
4) http://arxiv.org/abs/1501.03393
5) http://arxiv.org/abs/1203.2529
6) viewtopic.php?f=6&t=49&p=2545&hilit=third+rate#p2545
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Schmelzer's and Gill's mathematical nonsense
***
The following idiotic "critique" of my local model is by Richard D. Gill. He has posted it at this smear site: https://pubpeer.com/publications/AEF49D ... BA21F824B4
Each of Gill's idiotic misrepresentations of my Clifford-algebraic calculation can be disposed off easily. They only expose his incompetence. Let me do that one by one:
"According to (55) and (56), A(a, lambda) = lambda and B(b, lambda) = - lambda where lambda = +/-1. This should lead to E(a, b), computed in (60)-(68), equal to -1. But instead the author gets the result - a . b. How is it done?”
Eqs. (55) and (56) of my paper are trivially correct. But it is silly of Gill to write A(a, lambda) = lambda, because A = +/-1 is an outcome of a measurement result, whereas lambda is the orientation of the 3-sphere, which is the hidden variable in my model. And similarly it is silly of Gill to write B(b, lambda) = - lambda. Gill either deliberately writes this incorrectly to mislead the reader, or he is genuinely clueless about what is going on.
But it is true that A = +/-1 and B = -/+1 gives AB = -1 for a given lambda = +/-1. So naively, if one ignores the fact that lambda is an orientation of the 3-sphere and ignores the fact that initial spin-0 is conserved in any EPR-Bohm type experiment leading to my eq. (59), then one may mistakenly believe that E(a, b) = -1 always. But “E(a, b) = -1 always” can hold only if the conservation of spin angular momentum is violated. If one respects the conservation of spin angular momentum as one absolutely must, then inevitably E(a, b) = -a.b, as rigorously proven in eqs. (60) to (68) of my paper linked above. So there is absolutely no way to obtain anything other than the result E(a, b) = -a.b without either ignoring the geometry and topology of the 3-sphere or violating the conservation of angular momentum, or both.
“Notice formula (58) where s_1 and s_2 are argued to be equal, leading in (59) to L(s_1, lambda)L(s_2, lambda) = -1. This result is then substituted inside a double limit as s_1 converges to a and s_2 converges to b in the transition from equation (62) to (63).
So s_1 and s_2 are equal yet converge to different limits a and b.”
There is nothing mysterious about this. To begin with, s_1 and s_2 are not just “argued to be equal”, they are necessarily equal because of the conservation of spin angular momentum. This is clear from eq. (58) and the fundamental duality relation between the vectors s_i and bivectors L_i. In the standard notation of geometric algebra the duality relation is given by a /\ b = lambda I.(a x b). Thus the product vector a x b is orthogonal to the plane a /\ b, with lambda fixing one of the two possible sides of the bivectorial plane. Eq. (59) thus follows trivially from the conservation of spin angular momentum. In fact, one can take eq. (59) as a statement of the conservation of spin angular momentum. See also the revised version of the paper (arXiv v5) I have linked below for a more precise explanation of these facts.
Now the index 1 and 2 refers to the observation stations 1 and 2 of Alice and Bob. The measurement functions A(a, lambda) and B(b, lambda), in the standard local-realistic framework of Bell-1964, are defined by my eqs. (55) and (56). They correspond to two separate detection processes of Alice and Bob, by two different detectors, at two remote stations of Alice and Bob. There is therefore nothing mysterious about s_1 converging to the limit a, which is a detection direction chosen by Alice, and s_2 converging to limit b, which is a detection direction chosen by Bob. So two separate physical detection processes are taking place, at two separate remote observation stations. In summary, initially the two constituent spins, s_1 and s_2 are equal to each other, s_1 = s_2, because of the conservation of spin angular momentum of the initial spin-0 of the neutral pion (see Fig. 2 in the paper). These spins then go their separate ways towards the detectors of Alice and Bob. The detection processes of these spins are then defined as limiting processes in eqs. (55) and (56). In fact, my eqs. (55) and (56) are exactly the same as what Bell wrote down in eq. (9) of his 1964 paper, but my normalized spin components along the directions a and b are expressed as limits. But that is just a mathematically different expression for defining the same number (a normalized spin component). You can see this in more detail in eqs. (57) to (64) of the revised paper I have posted below, by comparing those with Bell’s eq. (9). I think Gill is capable of understanding this, but he disingenuously pretends to show that there is something fishy going on.
“But that is not enough. A second trick is put into play a few lines later. According to (57) we should have L(a, lambda)L(b, lambda) = D(a)D(b) independent of lambda, which means that the step from (65) to (66) can't be correct.”
There are no “tricks” in my paper. Gill uses such rhetorical devices deliberately to mislead the reader. For instance, lambda is not just a number. It is the orientation of the 3-sphere. It cannot disappear and reappear as Gill manipulates it to be. Nor does Gill respect the fact that L’s are bivectors, which are thus non-commutative, Clifford-algebraic objects. So, for instance, eq. (57) by no means say that
L(a, lambda)L(b, lambda) = D(a)D(b)
for both orientations lambda = +1 and lambda = -1. Let me stress again: lambda is the overall orientation (or parity) of the 3-sphere, which changes the handedness of the bivectors L(a) and L(b) with respect to the detectors. Gill is either genuinely ignorant to not understand this, or deliberately pretends to not understand it. In any case, the correct equations for lambda = +1 and lambda = -1 cases are the following:
L(a, lambda = +1) L(b, lambda = +1) = D(a) D(b)
but
L(a, lambda = -1)L(b, lambda = -1) = D(b) D(a),
because the change of the overall orientation of the 3-sphere changes the handedness of the spins L(a) and L(b) with respect to the detectors D(a) and D(b). Recall also that orientation of a manifold is a relative concept. See, for example, the explicit definition of orientation given in my IJTP paper.
So, contrary to Gill’s silly claim, the product D(a) D(b) is not independent of lambda, but its dependence on the orientation lambda is more subtle than Gill realizes. Orientation changes the order of the product. Consequently, there is nothing wrong with eq. (65) and (66). See also eqs. (70), (71), and (72) in the linked paper.
“To take that step he uses (50), but this contradicts (51) and (52). If L(a, lambda) = lambda I a and L(b, lambda) = lambda I b then L(a, lambda)L(b, lambda) = -ab independent of whether lambda = -1 or +1 (lambda and I both commute with a and b; lambda^2 = 1, I^2 = -1)."
Eq. (50) does not contradict eqs. (51) and (52). Gill’s argument here is quite silly. It shows that he has no understanding of even the most basic concepts in geometric (or Clifford) algebra, let alone those with respect to relative changes in the orientation of this algebra. Now L(a, lambda) L(b, lambda) = -ab is correct. But how on earth can –ab be independent of the orientation lambda if the product on LHS of the equation is with respect to a given lambda? In fact what he has missed again is the correct understanding of how the duality works between the vectors a and b and the bivectors L(a) and L(b) for different choices of lambda. It is quite funny how Gill manipulates lambda as if it was just a number, like +/-1. It is not just a number. It represents the orientation of the 3-sphere, taken as a physical space. To see his mistake, let us see what –ab actually is in terms of lambda. –ab is the geometric or Clifford product between the vectors a and b. We can expand that product as
-ab = -a.b - a /\ b.
But as we saw above a /\ b = lambda I.(a x b). So the geometric product –ab is by no means independent of lambda. It very much depends on the choice of lambda.
It is extremely unfortunate that physics has been paying such a high price for decades for the ignorance and incompetence of academic terrorist like Richard D. Gill.
*******************************************************************************************************************************************************************************************************
Note that I have now updated the article on the arXiv and added the following paragraph to it which includes eight new equations: https://arxiv.org/abs/1405.2355.

*******************************************************************************************************************************************************************************************************
The following idiotic "critique" of my local model is by Richard D. Gill. He has posted it at this smear site: https://pubpeer.com/publications/AEF49D ... BA21F824B4
Richard D. Gill wrote:
(The equation numbers refer to arXiv v4 of my paper: https://arxiv.org/pdf/1405.2355v4.pdf)
According to (55) and (56), A(a, lambda) = lambda and B(b, lambda) = - lambda where lambda = +/-1. This should lead to E(a, b), computed in (60)-(68), equal to -1. But instead the author gets the result - a . b. How is it done?
Notice formula (58) where s_1 and s_2 are argued to be equal, leading in (59) to L(s_1, lambda)L(s_2, lambda) = -1. This result is then substituted inside a double limit as s_1 converges to a and s_2 converges to b in the transition from equation (62) to (63).
So s_1 and s_2 are equal yet converge to different limits a and b.
But that is not enough. A second trick is put into play a few lines later. According to (57) we should have L(a, lambda)L(b, lambda) = D(a)D(b) independent of lambda, which means that the step from (65) to (66) can't be correct.
To take that step he uses (50), but this contradicts (51) and (52). If L(a, lambda) = lambda I a and L(b, lambda) = lambda I b then L(a, lambda)L(b, lambda) = -ab independent of whether lambda = -1 or +1 (lambda and I both commute with a and b; lambda^2 = 1, I^2 = -1)."
Each of Gill's idiotic misrepresentations of my Clifford-algebraic calculation can be disposed off easily. They only expose his incompetence. Let me do that one by one:
"According to (55) and (56), A(a, lambda) = lambda and B(b, lambda) = - lambda where lambda = +/-1. This should lead to E(a, b), computed in (60)-(68), equal to -1. But instead the author gets the result - a . b. How is it done?”
Eqs. (55) and (56) of my paper are trivially correct. But it is silly of Gill to write A(a, lambda) = lambda, because A = +/-1 is an outcome of a measurement result, whereas lambda is the orientation of the 3-sphere, which is the hidden variable in my model. And similarly it is silly of Gill to write B(b, lambda) = - lambda. Gill either deliberately writes this incorrectly to mislead the reader, or he is genuinely clueless about what is going on.
But it is true that A = +/-1 and B = -/+1 gives AB = -1 for a given lambda = +/-1. So naively, if one ignores the fact that lambda is an orientation of the 3-sphere and ignores the fact that initial spin-0 is conserved in any EPR-Bohm type experiment leading to my eq. (59), then one may mistakenly believe that E(a, b) = -1 always. But “E(a, b) = -1 always” can hold only if the conservation of spin angular momentum is violated. If one respects the conservation of spin angular momentum as one absolutely must, then inevitably E(a, b) = -a.b, as rigorously proven in eqs. (60) to (68) of my paper linked above. So there is absolutely no way to obtain anything other than the result E(a, b) = -a.b without either ignoring the geometry and topology of the 3-sphere or violating the conservation of angular momentum, or both.
“Notice formula (58) where s_1 and s_2 are argued to be equal, leading in (59) to L(s_1, lambda)L(s_2, lambda) = -1. This result is then substituted inside a double limit as s_1 converges to a and s_2 converges to b in the transition from equation (62) to (63).
So s_1 and s_2 are equal yet converge to different limits a and b.”
There is nothing mysterious about this. To begin with, s_1 and s_2 are not just “argued to be equal”, they are necessarily equal because of the conservation of spin angular momentum. This is clear from eq. (58) and the fundamental duality relation between the vectors s_i and bivectors L_i. In the standard notation of geometric algebra the duality relation is given by a /\ b = lambda I.(a x b). Thus the product vector a x b is orthogonal to the plane a /\ b, with lambda fixing one of the two possible sides of the bivectorial plane. Eq. (59) thus follows trivially from the conservation of spin angular momentum. In fact, one can take eq. (59) as a statement of the conservation of spin angular momentum. See also the revised version of the paper (arXiv v5) I have linked below for a more precise explanation of these facts.
Now the index 1 and 2 refers to the observation stations 1 and 2 of Alice and Bob. The measurement functions A(a, lambda) and B(b, lambda), in the standard local-realistic framework of Bell-1964, are defined by my eqs. (55) and (56). They correspond to two separate detection processes of Alice and Bob, by two different detectors, at two remote stations of Alice and Bob. There is therefore nothing mysterious about s_1 converging to the limit a, which is a detection direction chosen by Alice, and s_2 converging to limit b, which is a detection direction chosen by Bob. So two separate physical detection processes are taking place, at two separate remote observation stations. In summary, initially the two constituent spins, s_1 and s_2 are equal to each other, s_1 = s_2, because of the conservation of spin angular momentum of the initial spin-0 of the neutral pion (see Fig. 2 in the paper). These spins then go their separate ways towards the detectors of Alice and Bob. The detection processes of these spins are then defined as limiting processes in eqs. (55) and (56). In fact, my eqs. (55) and (56) are exactly the same as what Bell wrote down in eq. (9) of his 1964 paper, but my normalized spin components along the directions a and b are expressed as limits. But that is just a mathematically different expression for defining the same number (a normalized spin component). You can see this in more detail in eqs. (57) to (64) of the revised paper I have posted below, by comparing those with Bell’s eq. (9). I think Gill is capable of understanding this, but he disingenuously pretends to show that there is something fishy going on.
“But that is not enough. A second trick is put into play a few lines later. According to (57) we should have L(a, lambda)L(b, lambda) = D(a)D(b) independent of lambda, which means that the step from (65) to (66) can't be correct.”
There are no “tricks” in my paper. Gill uses such rhetorical devices deliberately to mislead the reader. For instance, lambda is not just a number. It is the orientation of the 3-sphere. It cannot disappear and reappear as Gill manipulates it to be. Nor does Gill respect the fact that L’s are bivectors, which are thus non-commutative, Clifford-algebraic objects. So, for instance, eq. (57) by no means say that
L(a, lambda)L(b, lambda) = D(a)D(b)
for both orientations lambda = +1 and lambda = -1. Let me stress again: lambda is the overall orientation (or parity) of the 3-sphere, which changes the handedness of the bivectors L(a) and L(b) with respect to the detectors. Gill is either genuinely ignorant to not understand this, or deliberately pretends to not understand it. In any case, the correct equations for lambda = +1 and lambda = -1 cases are the following:
L(a, lambda = +1) L(b, lambda = +1) = D(a) D(b)
but
L(a, lambda = -1)L(b, lambda = -1) = D(b) D(a),
because the change of the overall orientation of the 3-sphere changes the handedness of the spins L(a) and L(b) with respect to the detectors D(a) and D(b). Recall also that orientation of a manifold is a relative concept. See, for example, the explicit definition of orientation given in my IJTP paper.
So, contrary to Gill’s silly claim, the product D(a) D(b) is not independent of lambda, but its dependence on the orientation lambda is more subtle than Gill realizes. Orientation changes the order of the product. Consequently, there is nothing wrong with eq. (65) and (66). See also eqs. (70), (71), and (72) in the linked paper.
“To take that step he uses (50), but this contradicts (51) and (52). If L(a, lambda) = lambda I a and L(b, lambda) = lambda I b then L(a, lambda)L(b, lambda) = -ab independent of whether lambda = -1 or +1 (lambda and I both commute with a and b; lambda^2 = 1, I^2 = -1)."
Eq. (50) does not contradict eqs. (51) and (52). Gill’s argument here is quite silly. It shows that he has no understanding of even the most basic concepts in geometric (or Clifford) algebra, let alone those with respect to relative changes in the orientation of this algebra. Now L(a, lambda) L(b, lambda) = -ab is correct. But how on earth can –ab be independent of the orientation lambda if the product on LHS of the equation is with respect to a given lambda? In fact what he has missed again is the correct understanding of how the duality works between the vectors a and b and the bivectors L(a) and L(b) for different choices of lambda. It is quite funny how Gill manipulates lambda as if it was just a number, like +/-1. It is not just a number. It represents the orientation of the 3-sphere, taken as a physical space. To see his mistake, let us see what –ab actually is in terms of lambda. –ab is the geometric or Clifford product between the vectors a and b. We can expand that product as
-ab = -a.b - a /\ b.
But as we saw above a /\ b = lambda I.(a x b). So the geometric product –ab is by no means independent of lambda. It very much depends on the choice of lambda.
It is extremely unfortunate that physics has been paying such a high price for decades for the ignorance and incompetence of academic terrorist like Richard D. Gill.
*******************************************************************************************************************************************************************************************************
Note that I have now updated the article on the arXiv and added the following paragraph to it which includes eight new equations: https://arxiv.org/abs/1405.2355.

*******************************************************************************************************************************************************************************************************
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Schmelzer's and Gill's mathematical nonsense
I think this is the crux of the matter, and the source of all misdirection:
" ... lambda is not just a number. It is the orientation of the 3-sphere. It cannot disappear and reappear as Gill manipulates it to be."
Gill ran the same nonsense on Karl Hess. Claiming that "lambda can be anything", shows a profound innocence of the meaning of independent and dependent variables. Unfortunately, it is a belief shared by better minds -- such as Bell, Leggett and Myrvold.
" ... lambda is not just a number. It is the orientation of the 3-sphere. It cannot disappear and reappear as Gill manipulates it to be."
Gill ran the same nonsense on Karl Hess. Claiming that "lambda can be anything", shows a profound innocence of the meaning of independent and dependent variables. Unfortunately, it is a belief shared by better minds -- such as Bell, Leggett and Myrvold.
- thray
- Posts: 143
- Joined: Sun Feb 16, 2014 6:30 am
Re: Schmelzer's and Gill's mathematical nonsense
Tom, re dependent and independent variables under EPRB, I've opened this: viewtopic.php?f=6&t=284
Xray
Xray
- Xray
- Posts: 44
- Joined: Mon Apr 21, 2014 2:23 pm
Re: Schmelzer's and Gill's mathematical nonsense
***
It appears that Richard D. Gill is determined to continue exhibiting his incompetence in elementary mathematics. He has posted more idiotic comments on the same smear site, PubPeer, but now on the latest version of my paper. Let me remind everyone once again that Gill is not a physicist. He is a statistician, and not a very good one. His comments below again prove how incompetent Gill really is in elementary mathematics. And not surprisingly, he has no grasp of basic physics. So here we go:
Gill is talking about the equations I have posted above. Let me post them again here for convenience:

There is of course nothing at all wrong with these simple limits. Any schoolchild can understand them. Anyone other than Richard D. Gill can understand them.
What Gill is questioning here is the following elementary equality.
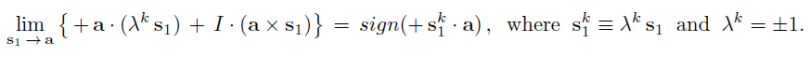
Note that in his first long paragraph above Gill employs his usual trick of misleading the reader. He tries to give the impression that he is only innocently simplifying (59) for the benefit of the reader. In fact, what he is doing is taking the reader a step away from what eq. (59) actually says; which is a limit s_1 going to a within a quaternion. A more charitable way to see Gill's attempt to deceitfully rewrite (59) is to see it as due to his complete lack of understanding of basic Clifford algebra.
Perhaps a more detailed view of quaternions within S^3 may help to see what is going on in these limits: https://www.academia.edu/attachments/45 ... r-dropdown
In conclusion, contrary to Gill's claim, the equality between (59) and (60) makes perfect sense within S^3, and the final result is thus perfectly consistent with (54).
Moreover, this whole exercise is added only to show consistency with Bell's original model. The sign function does not play any role in my Clifford-algebraic model.
***
It appears that Richard D. Gill is determined to continue exhibiting his incompetence in elementary mathematics. He has posted more idiotic comments on the same smear site, PubPeer, but now on the latest version of my paper. Let me remind everyone once again that Gill is not a physicist. He is a statistician, and not a very good one. His comments below again prove how incompetent Gill really is in elementary mathematics. And not surprisingly, he has no grasp of basic physics. So here we go:
Richard D. Gill wrote:
Now version 5 is online: https://arxiv.org/pdf/1405.2355v5.pdf
It contains some new material, in particular, the derivations (57)-(60) and (61)-(64) on page 8. In (57)-(60), the limit is taken as s_1 converges to a of some expression which depends on s_1, a and lambda. Up to (59) everything seems to be OK. In (59) we have a limit of a sum of two terms. Going from (59) to (60) the following seems to have happened. The limit of a sum of two terms is rewritten as a sum of two limits, one for each of the two terms separately. The second of the two limits is evaluated, the result is zero. The first limit is however not evaluated: instead, no limit is taken at all, so that the end result still depends on the dummy variable s_1.
The expression concerned is continuous in s_1, a and lambda and the limit can therefore be computed by simply evaluating it with s_1 set equal to a. That results in lambda, as already claimed in (54).
So the step from (59) to (60) is non-sense, and the final result moreover contradicts (54).
Gill is talking about the equations I have posted above. Let me post them again here for convenience:

There is of course nothing at all wrong with these simple limits. Any schoolchild can understand them. Anyone other than Richard D. Gill can understand them.
What Gill is questioning here is the following elementary equality.
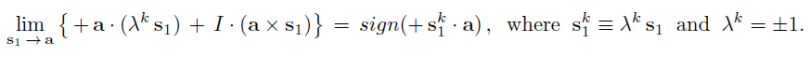
Note that in his first long paragraph above Gill employs his usual trick of misleading the reader. He tries to give the impression that he is only innocently simplifying (59) for the benefit of the reader. In fact, what he is doing is taking the reader a step away from what eq. (59) actually says; which is a limit s_1 going to a within a quaternion. A more charitable way to see Gill's attempt to deceitfully rewrite (59) is to see it as due to his complete lack of understanding of basic Clifford algebra.
Perhaps a more detailed view of quaternions within S^3 may help to see what is going on in these limits: https://www.academia.edu/attachments/45 ... r-dropdown
In conclusion, contrary to Gill's claim, the equality between (59) and (60) makes perfect sense within S^3, and the final result is thus perfectly consistent with (54).
Moreover, this whole exercise is added only to show consistency with Bell's original model. The sign function does not play any role in my Clifford-algebraic model.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Schmelzer's and Gill's mathematical nonsense
Joy Christian wrote:***Richard D. Gill wrote:
Now version 5 is online: https://arxiv.org/pdf/1405.2355v5.pdf
It contains some new material, in particular, the derivations (57)-(60) and (61)-(64) on page 8. In (57)-(60), the limit is taken as s_1 converges to a of some expression which depends on s_1, a and lambda. Up to (59) everything seems to be OK. In (59) we have a limit of a sum of two terms. Going from (59) to (60) the following seems to have happened. The limit of a sum of two terms is rewritten as a sum of two limits, one for each of the two terms separately. The second of the two limits is evaluated, the result is zero. The first limit is however not evaluated: instead, no limit is taken at all, so that the end result still depends on the dummy variable s_1.
The expression concerned is continuous in s_1, a and lambda and the limit can therefore be computed by simply evaluating it with s_1 set equal to a. That results in lambda, as already claimed in (54).
So the step from (59) to (60) is non-sense, and the final result moreover contradicts (54).
After many months of staying out of the "Bell Wars," I finally got dragged into them at Retraction Watch when some folks started asking questions about poor little old me who was just sitting around minding my own business.
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Schmelzer's and Gill's mathematical nonsense
Yablon wrote:After many months of staying out of the "Bell Wars," I finally got dragged into them at Retraction Watch when some folks started asking questions about poor little old me who was just sitting around minding my own business.Following some dialogue which you may follow at http://retractionwatch.com/2016/09/30/p ... /#comments in which I offered to mediate the dispute between Joy and Richard (which I have really tried to stay out of), Richard posed the same question above, to me. So, I did the math that Richard critiqued by which Joy goes from (59) to (60). My calculation may be seen at https://jayryablon.files.wordpress.com/ ... jcrg-2.pdf. I truly hope this is helpful to everyone. Beyond my desire to end a war between two people and the two "camps" they have come to represent, I feel a duty to science as a scientist to try to help resolve this quagmire if there is any chance that I can do so. Jay
Thank you very much, Jay. Your analysis is indeed helpful. There is of course nothing deep about the issue. But it is good to have an independent analysis for all to see.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Schmelzer's and Gill's mathematical nonsense
Yablon wrote:After many months of staying out of the "Bell Wars," I finally got dragged into them at Retraction Watch when some folks started asking questions about poor little old me who was just sitting around minding my own business.Following some dialogue which you may follow at http://retractionwatch.com/2016/09/30/p ... /#comments in which I offered to mediate the dispute between Joy and Richard (which I have really tried to stay out of), Richard posed the same question above, to me. So, I did the math that Richard critiqued by which Joy goes from (59) to (60). My calculation may be seen at https://jayryablon.files.wordpress.com/ ... jcrg-2.pdf. I truly hope this is helpful to everyone. Beyond my desire to end a war between two people and the two "camps" they have come to represent, I feel a duty to science as a scientist to try to help resolve this quagmire if there is any chance that I can do so. Jay
Be very careful about engaging with Gill, Jay.
http://www.naturalnews.com/036112_socio ... uence.html
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Schmelzer's and Gill's mathematical nonsense
I enjoyed that very much, Jay!
It should be noted that the physical element -- backtracking, or recursion -- is native to analysis, and not inserted ad hoc, implied in the topology on which Joy bases his measurement framework. That Bell's theorem has an analytical foundation is something that I don't think Richard can get his mind around. If you can show him the way, may we all be the better for it.
All best,
Tom
It should be noted that the physical element -- backtracking, or recursion -- is native to analysis, and not inserted ad hoc, implied in the topology on which Joy bases his measurement framework. That Bell's theorem has an analytical foundation is something that I don't think Richard can get his mind around. If you can show him the way, may we all be the better for it.
All best,
Tom
- thray
- Posts: 143
- Joined: Sun Feb 16, 2014 6:30 am
Re: Schmelzer's and Gill's mathematical nonsense
Joy Christian wrote:Yablon wrote:After many months of staying out of the "Bell Wars," I finally got dragged into them at Retraction Watch when some folks started asking questions about poor little old me who was just sitting around minding my own business.Following some dialogue which you may follow at http://retractionwatch.com/2016/09/30/p ... /#comments in which I offered to mediate the dispute between Joy and Richard (which I have really tried to stay out of), Richard posed the same question above, to me. So, I did the math that Richard critiqued by which Joy goes from (59) to (60). My calculation may be seen at https://jayryablon.files.wordpress.com/ ... jcrg-2.pdf. I truly hope this is helpful to everyone. Beyond my desire to end a war between two people and the two "camps" they have come to represent, I feel a duty to science as a scientist to try to help resolve this quagmire if there is any chance that I can do so. Jay
Thank you very much, Jay. Your analysis is indeed helpful. There is of course nothing deep about the issue. But it is good to have an independent analysis for all to see.
***
Hi again to Joy and all. Richard send me a follow up email based on the above, and I have included this reply from him and my further analysis at https://jayryablon.files.wordpress.com/ ... jcrg-3.pdf. Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Schmelzer's and Gill's mathematical nonsense
FrediFizzx wrote:Be very careful about engaging with Gill, Jay.
http://www.naturalnews.com/036112_socio ... uence.html
I also warned Jay about Gill.
Gill's latest attempt to not understand my new equations above is no different from all of his previous attempts. There is absolutely nothing mysterious about the two limits in my eqs. (54) and (55). Any schoolchild can understand that one and the same vector s can have normalised components along two different vectors, say a and b. In my eqs. (54) and (55) I am simply calculating a normalised component of s along a and a normalised component of s along b, just as how Bell calculated in 1964.
***
PS: I just saw your latest post, Jay, which you posted while I was typing this one. Thank you very much indeed for your efforts.
PPS: I should add, however, that over the past several years (starting from 2007 when I was at the Perimeter Institute) several of us have shown all of Gill's "objections" to my model to be misguided or plane wrong, and have disposed them off one by one, often with detailed refutations. But year after year Gill keeps coming back with new objections, while endlessly repeating the already debunked ones. So I am highly sceptical that he will ever stop. He will keep coming back like the Terminator.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Schmelzer's and Gill's mathematical nonsense
Yablon wrote:Hi again to Joy and all. Richard send me a follow up email based on the above, and I have included this reply from him and my further analysis at https://jayryablon.files.wordpress.com/ ... jcrg-3.pdf. Jay
Hi Jay,
Once again Gill seems to still have no physical concept of what happens in the EPR-Bohm scenario. The answer is simple. When the particle pair is created s1=s2=s from the common origin. Then with the first particle s1 goes to a and with the second particle s2 goes to b. So s1 does not necessarily equal s2 upon detection therefore a does not necessarily equal b. He has been told this several times but ignores it thinking everything in math has to happen all at once. Perhaps Joy now needs to add some kind of time parameter. But it is completely clear to most people that know how the scenario works physically.
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Schmelzer's and Gill's mathematical nonsense
***
Let me summarise Jay's argument refuting Gill's longstanding claim against my model, because it is instructive to compare Jay's analytical ability against Gill's. Jay has used a brilliant judo-type manoeuvre to refute Gill's claim in his own silly game, which I now summarise in the notation of my paper: https://arxiv.org/abs/1405.2355
From Jay's PDF attached above, Gill privately raised the following rhetorical question to Jay:
Those who have followed the back and forth between Gill and I over the years know very well that on many occasions Gill has maintained that my local model works only for the very special case of a = b, for which the correlations are always E(a, a) = -a.a = -1. In fact Scott Aaronson has also maintained essentially the same claim.
One variant of their argument goes something like this. From the definitions of my measurement functions we immediately recognise that
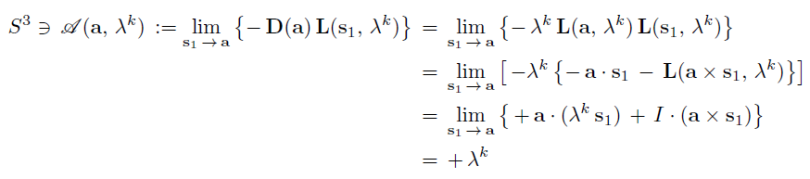
and
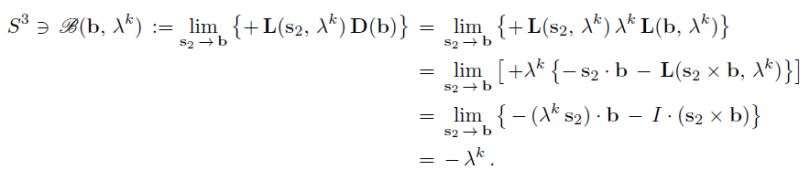
That is true. So, their argument goes, we can see from the fourth lines of the above two limits that the product AB = +lambda x -lambda = -1, since lambda^2 = +1.
Therefore, they claim, either the correlations must always be E(a, b) = -1, or the only possible vectors for which my model makes sense are a = b, violating "freedom."
Now Jay says: Fine, let us figure out what constraint the fourth lines of the above two limits actually put on the possible choices of the vectors a and b. Because of the fourth lines of the above two limits we can equate the third lines of the limits as follows, and then evaluate the limits on both sides to get the constraints on a and b:
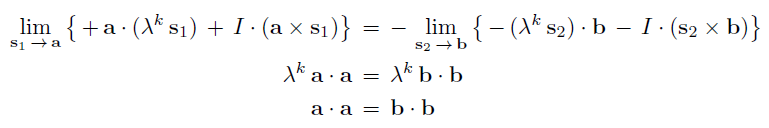
Well, it is crystal clear from the last equation that the only constraint that must be maintained on a and b is that they both must have the same normalisation. But that they certainly do, because they are both unit vectors in my model. There is no other restriction on what directions Alice and Bob may choose to perform their respective experiments. They do not have to set a = b. In other words, Jay has quite convincingly demonstrated that Gill's argument has been nonsense all along.
***
Let me summarise Jay's argument refuting Gill's longstanding claim against my model, because it is instructive to compare Jay's analytical ability against Gill's. Jay has used a brilliant judo-type manoeuvre to refute Gill's claim in his own silly game, which I now summarise in the notation of my paper: https://arxiv.org/abs/1405.2355
From Jay's PDF attached above, Gill privately raised the following rhetorical question to Jay:
Richard D. Gill wrote:
I agree that if a = s_1 then indeed we can get (60)
Similarly if b = s_2 we can get (64)
In (65) Joy argues that s_1 = s_2
Do you think he wants a = b to be true, as well?
Those who have followed the back and forth between Gill and I over the years know very well that on many occasions Gill has maintained that my local model works only for the very special case of a = b, for which the correlations are always E(a, a) = -a.a = -1. In fact Scott Aaronson has also maintained essentially the same claim.
One variant of their argument goes something like this. From the definitions of my measurement functions we immediately recognise that
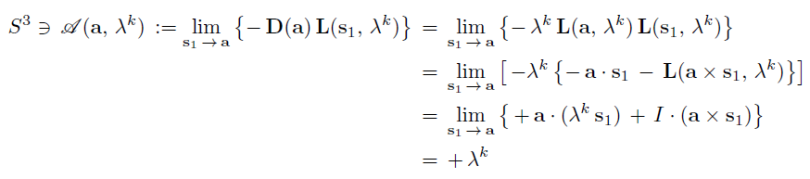
and
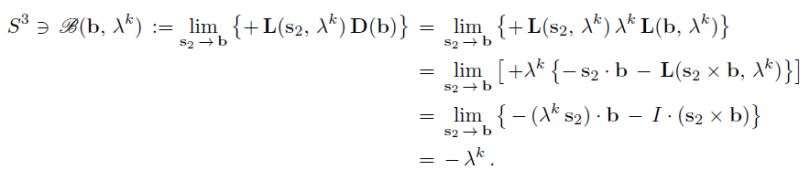
That is true. So, their argument goes, we can see from the fourth lines of the above two limits that the product AB = +lambda x -lambda = -1, since lambda^2 = +1.
Therefore, they claim, either the correlations must always be E(a, b) = -1, or the only possible vectors for which my model makes sense are a = b, violating "freedom."
Now Jay says: Fine, let us figure out what constraint the fourth lines of the above two limits actually put on the possible choices of the vectors a and b. Because of the fourth lines of the above two limits we can equate the third lines of the limits as follows, and then evaluate the limits on both sides to get the constraints on a and b:
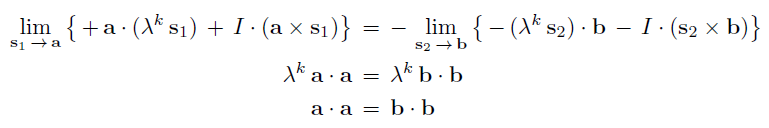
Well, it is crystal clear from the last equation that the only constraint that must be maintained on a and b is that they both must have the same normalisation. But that they certainly do, because they are both unit vectors in my model. There is no other restriction on what directions Alice and Bob may choose to perform their respective experiments. They do not have to set a = b. In other words, Jay has quite convincingly demonstrated that Gill's argument has been nonsense all along.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Schmelzer's and Gill's mathematical nonsense
Joy Christian wrote:***
Let me summarise Jay's argument refuting Gill's longstanding claim against my model, because it is instructive to compare Jay's analytical ability against Gill's. Jay has used a brilliant judo-type manoeuvre to refute Gill's claim in his own silly game, which I now summarise in the notation of my paper: https://arxiv.org/abs/1405.2355
To keep this as simple as possible, my analysis is this:
Richard has maintained that setting
Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Schmelzer's and Gill's mathematical nonsense
***
Thanks, Jay. A small correction in notation so that people don't get confused. In standard notation A and B are measurement outcomes and a and b are the vector directions. So what you mean is that the constraint is not a = b, but |a| = |b|, which is harmless, because all vectors in the model are unit vectors to begin with.
***
Thanks, Jay. A small correction in notation so that people don't get confused. In standard notation A and B are measurement outcomes and a and b are the vector directions. So what you mean is that the constraint is not a = b, but |a| = |b|, which is harmless, because all vectors in the model are unit vectors to begin with.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Schmelzer's and Gill's mathematical nonsense
This is a copy of a reply that I just had posted onto Retraction watch (with one or two typos corrected here). Jay
On October 10, 2016 at 1:04 am in a post here at RW I offered to try to help mediate the dispute between Joy Christian and Richard Gill, given that I am good terms with both. Richard accepted this in a post at October 10, 2016 at 9:32 am, and Joy has also agreed. So since then I have been trying to winnow down the dispute as clearly as possible in my own mind, and to provide my analysis of the salient points. While I understand Joy’s outrage about the retraction, in accordance with Donald Graft’s recommendation at October 9, 2016 at 11:41 pm I have advised Joy to stay away from personal attacks here at RW and focus on the science, and he is cool with that. I hope that will enable any posts he makes which stay on the science and not on personalities will be cleared onto RW, because, after all, it is his paper that is the topic of this thread. So, in the waning hours before I begin Yom Kippur observance and turn into a pumpkin for a couple of days, I would like to briefly summarize what I have learned so far from my communications with both Joy and Richard, which have been conducted privately and separately by email with each. I will try to do this in a clear and concise way.
In reference to Joy’s paper at https://arxiv.org/pdf/1405.2355v5.pdf, Richard first maintained in his RW post of October 10, 2016 at 9:32 am that Joy’s “step from (59) to (60) is non-sense, and the final result moreover contradicts (54).” As a consequence of the derivation I provided at https://jayryablon.files.wordpress.com/ ... jcrg-2.pdf, Richard agreed in a private email to me that in the steps from Joy’s (59) to (60) for Alice and likewise from (63) to (64) for Bob are valid, if we set a=s_1 and b=s_2 when taking the limits in equations (57) to (64). So we are past that.
Richard has next argued that if s_1–> a and s_2 –> b when taking the limits, then because of the further constraint s_1=s_2 that Joy introduces at (65) to conserve angular momentum for the doublet that emerges from the singlet, then this implies a=b, which looks on the surface to be a trivial consequence of combining the foregoing relations in this sentence. If a=b in fact, then Joy’s work would fail, because that would force Alice and Bob to align their detectors which defeats the premise of the EPR experiment that the two parties choose their detector directions independently without conspiracy.
Now, while I agree with Richard that setting s_1=s_2 does serve also to constrain a and b in relation to one another, I find that the constraint imposed in fact is that the magnitudes must obey |a|=|b|. But there is no requirement to have a=b. In other words, the constraint s_1=s_2 in (65) only requires that a and b have the same magnitude which is a weaker condition, but it does not require the stronger condition that they have the same direction. I have laid out my deduction of this at https://jayryablon.files.wordpress.com/ ... jcrg-3.pdf for anybody to review in detail if they wish. Because a and b are unit vectors such that |a|=|b|=1, this condition is already built in to the whole model. And even if these were not unit vectors, |a|=|b| is merely a normalization requirement, nothing more. All the salient issues in EPR are about direction, not magnitude.
My discussions with Richard and Joy are continuing, and I will report on them here at RW as I am able to gain further clarification. However, to the extent that this retraction may have been based on a belief that a=b is a consequence of angular momentum conservation, it is my opinion that the retraction is scientifically-flawed, because in fact the only consequence of conserving angular momentum after the singlet becomes a doublet is that the magnitudes must obey |a|=|b|. Not a=b.
On October 10, 2016 at 1:04 am in a post here at RW I offered to try to help mediate the dispute between Joy Christian and Richard Gill, given that I am good terms with both. Richard accepted this in a post at October 10, 2016 at 9:32 am, and Joy has also agreed. So since then I have been trying to winnow down the dispute as clearly as possible in my own mind, and to provide my analysis of the salient points. While I understand Joy’s outrage about the retraction, in accordance with Donald Graft’s recommendation at October 9, 2016 at 11:41 pm I have advised Joy to stay away from personal attacks here at RW and focus on the science, and he is cool with that. I hope that will enable any posts he makes which stay on the science and not on personalities will be cleared onto RW, because, after all, it is his paper that is the topic of this thread. So, in the waning hours before I begin Yom Kippur observance and turn into a pumpkin for a couple of days, I would like to briefly summarize what I have learned so far from my communications with both Joy and Richard, which have been conducted privately and separately by email with each. I will try to do this in a clear and concise way.
In reference to Joy’s paper at https://arxiv.org/pdf/1405.2355v5.pdf, Richard first maintained in his RW post of October 10, 2016 at 9:32 am that Joy’s “step from (59) to (60) is non-sense, and the final result moreover contradicts (54).” As a consequence of the derivation I provided at https://jayryablon.files.wordpress.com/ ... jcrg-2.pdf, Richard agreed in a private email to me that in the steps from Joy’s (59) to (60) for Alice and likewise from (63) to (64) for Bob are valid, if we set a=s_1 and b=s_2 when taking the limits in equations (57) to (64). So we are past that.
Richard has next argued that if s_1–> a and s_2 –> b when taking the limits, then because of the further constraint s_1=s_2 that Joy introduces at (65) to conserve angular momentum for the doublet that emerges from the singlet, then this implies a=b, which looks on the surface to be a trivial consequence of combining the foregoing relations in this sentence. If a=b in fact, then Joy’s work would fail, because that would force Alice and Bob to align their detectors which defeats the premise of the EPR experiment that the two parties choose their detector directions independently without conspiracy.
Now, while I agree with Richard that setting s_1=s_2 does serve also to constrain a and b in relation to one another, I find that the constraint imposed in fact is that the magnitudes must obey |a|=|b|. But there is no requirement to have a=b. In other words, the constraint s_1=s_2 in (65) only requires that a and b have the same magnitude which is a weaker condition, but it does not require the stronger condition that they have the same direction. I have laid out my deduction of this at https://jayryablon.files.wordpress.com/ ... jcrg-3.pdf for anybody to review in detail if they wish. Because a and b are unit vectors such that |a|=|b|=1, this condition is already built in to the whole model. And even if these were not unit vectors, |a|=|b| is merely a normalization requirement, nothing more. All the salient issues in EPR are about direction, not magnitude.
My discussions with Richard and Joy are continuing, and I will report on them here at RW as I am able to gain further clarification. However, to the extent that this retraction may have been based on a belief that a=b is a consequence of angular momentum conservation, it is my opinion that the retraction is scientifically-flawed, because in fact the only consequence of conserving angular momentum after the singlet becomes a doublet is that the magnitudes must obey |a|=|b|. Not a=b.
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Schmelzer's and Gill's mathematical nonsense
Joy, I think you need to add a time parameter to your formulation so that it is more clear about the creation event and the detection events.
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Schmelzer's and Gill's mathematical nonsense
FrediFizzx wrote:Joy, I think you need to add a time parameter to your formulation so that it is more clear about the creation event and the detection events.
The time parameter is already there, albeit it is implicit. I am reproducing a short paragraph that appears just below eq. (12) in https://arxiv.org/abs/1405.2355
Since we are primarily concerned with a galactic, solar, or terrestrial scenario, in what follows we will restrict our
attention to the current epoch of the cosmos by setting the scale factor a(t) = 1 in the solution (9). Moreover, we will
not be using the time coordinate in (9) explicitly. Instead, we will follow the practice of defining the measurement
events in terms of the initial and final instants of time, as usually done within the context of Bell’s local model [1][3].
Readers who are not familiar with this practice are urged to review the Appendix below before proceeding further [8].
In other words, anyone who is familiar with the Bell literature, as the "expert" Richard D. Gill should be, should not have any difficulty in understanding the model.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
70 posts
• Page 1 of 4 • 1, 2, 3, 4
Return to Sci.Physics.Foundations
Who is online
Users browsing this forum: No registered users and 236 guests

