How to generate correlations of ANY strength: Linear to Box
As we had been discussing, here is the most accurate simulation of my 3-sphere model for the EPR-Bohm correlation: http://rpubs.com/jjc/13965.
The theoretical description and conceptual understanding of the 3-sphere model can be found on my blog: http://libertesphilosophica.info/blog/.
The initial function (or the cumulative distribution function, if you like), as defined in eq. (7) of this document, has been taken now to be
\,=\,-1\,+\,\frac{2}{\sqrt{1+\frac{3\,\theta_o}{\pi}\;}\;}\;,\;\;{\rm with}\;\, \theta_o\,\in\,[0,\;\pi]) .
.
Not surprisingly, it turns out that the strength of the correlation generated by this function can be changed simply by changing the geometric constant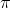 .
.
For example, try replacing the geometric constant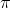 under the square-root in the above simulation with the following options:
under the square-root in the above simulation with the following options:
Linear: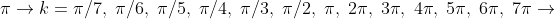 Box.
Box.
This further supports my view that quantum correlations are purely geometrical and topological effects. They have nothing to do with non-locality or non-reality.
The theoretical description and conceptual understanding of the 3-sphere model can be found on my blog: http://libertesphilosophica.info/blog/.
The initial function (or the cumulative distribution function, if you like), as defined in eq. (7) of this document, has been taken now to be
Not surprisingly, it turns out that the strength of the correlation generated by this function can be changed simply by changing the geometric constant
For example, try replacing the geometric constant
Linear:
This further supports my view that quantum correlations are purely geometrical and topological effects. They have nothing to do with non-locality or non-reality.
