E(a,b) is incompletely specified. Are the particles relevant or not? If Alice and Bob set their devices to "a" and "b" respectively, it does not give us anything without particles. Even with particles, we do not get a unique value for E(a,b) unless we have a specific distribution of particles.
)
Not to talk of the function A(a). They too are ill specified since the same function operating on a different particle may produce a different result, thus
)
And even the same particle at a different time may produce a different outcome, thus
)
Same for
)
Once you start filling out the missing details, it becomes obvious that very often the whole Bell discussion is really one of "apples" vs "oranges".
For example, in QM, the symbols A(a), A(a'), B(b), B(b') are operators not outcomes which need to be converted to outcomes. before averaging. Which means the QM expression
B(b)> + <A(a')B(b')> + <A(a')B(b)> - <A(a)B(b')>)
is a completely different Beast from a CHSH expression like
B(b)> + <A(a')B(b')> + <A(a')B(b)> - <A(a)B(b')>)
The QM operators must operate on something (a wavefunction of a system) in order to produce measurable outcomes. Since in [A(a), A(a')] =/=0, and [B(b), B(b')] =/=0, therefore
[A(a)B(b),A(a')B(b) ] =/=0, and [A(a)B(b),A(a)B(b') ] =/=0 etc there is a cyclical non-commutation of the joined operators
the above expression from QM can not represent a simultaneous measurement on the same ensemble. Or if it is assumed to apply to the same ensemble as the CHSH would imply, then the measurement result for
B(b)> + <A(a')B(b')> + <A(a')B(b)> - <A(a)B(b')>)
would give a different result (which would not violate the CHSH) than the sum of the separately measured terms.
Therefore the QM expression is therefore equivalent to
⟨A₁B₁⟩ + ⟨A₂B’₂⟩ + ⟨A’₃B₃⟩ – ⟨A’₄B’₄⟩
in case anyone was doubting that.
Butterfield wrote:What Bell objects to in both von Neumann's and Kochen and Specker's no-go theorems is arbitrary assumptions about how the results of measurements undertaken with incompatible experimental arrangements would turn out. For von Neumann, it is the assumption that if an observable C is actually measured, where
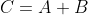
and
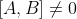
, then had A instead been measured, or B, their results would have been such as to sum to the value actually obtained for C. For Kochen and Specker, who adopt von Neumann's linearity requirement only when
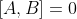
, it is the assumption that the results of measuring C would be the same independent of whether C is measured along with A and B or in the context of measuring some other pair of compatible observables A' and B' such that C = A' + B'. What makes these assumptions arbitrary, for Bell, is that the results of measuring observables A,B,C, ... might not reveal separate pre-existing values for them, but rather realize mere dispositions of the system to produce those results in the context of specific experimental arrangements they are obtained in. In other words, the 'observables' at issue need not all be beables in the hidden-variables interpretations the no-go theorems seek to rule out.
Bell wrote:It was not the objective measurable predictions of quantum mechanics which ruled out hidden variables. It was the arbitrary assumption of a particular (and impossible) relation between the results of incompatible measurements either of which might be made on a given occasion but only one of which can in fact be made.
Yet the von Neumann proof, if you actually come to grips with it, falls apart in your hands! There is nothing to it. It’s not just flawed, it’s silly. If you look at the assumptions it made, it does not hold up for a moment. It’s the work of a mathematician, and he makes assumptions that have a mathematical symmetry to them. When you translate them into terms of physical disposition, they’re nonsense. You may quote me on that: the proof of von Neumann is not merely false but foolish.