- Code: Select all
//Adaptation of Albert Jan Wonnink's original code
//http://challengingbell.blogspot.com/2015/03/numerical-validation-of-vanishing-of.html
//Joy Christian's S^3 GA Model Correlations
function getRandomLambda()
{
if( rand()>0.5) {return 1;} else {return -1;}
}
function getRandomUnitVector() //uniform random unit vector:
//http://mathworld.wolfram.com/SpherePointPicking.html
{
v=randGaussStd()*e1+randGaussStd()*e2+ 0.0000*e3;
return normalize(v);
}
batch test()
{
set_window_title("Test of Joy Christian's S^3 Local-Realistic Model");
N=50000; //number of iterations (trials)
I=e1^e2^e3;
for(nn=0;nn<N;nn=nn+1) //perform the experiment N times
{
a=getRandomUnitVector();
b=getRandomUnitVector();
lambda=getRandomLambda(); //lambda is a fair coin,
//resulting in +1 or -1
mu=lambda * I; //calculate the lambda dependent mu
A=(-I.a)(mu.a); //Eq.(54)of arXiv:1405.2355
B=(mu.b)(I.b); //Eq.(55)of arXiv:1405.2355
La=A/a; //Part of eq.(72)of arXiv:1405.2355
Lb=B/b; //Part of eq.(72)of arXiv:1405.2355
q=0;
if(lambda==1) {q=(La Lb);} else {q=(Lb La);}
print(corrs=scalar(q), "f"); //Output the correlations
angleA=atan2(scalar(a/e1), scalar(a/e2))*180/pi;
angleB=atan2(scalar(b/e1), scalar(b/e2))*180/pi;
angle=abs(angleB - angleA);
print(angle); //Output the angles
}
prompt();
}
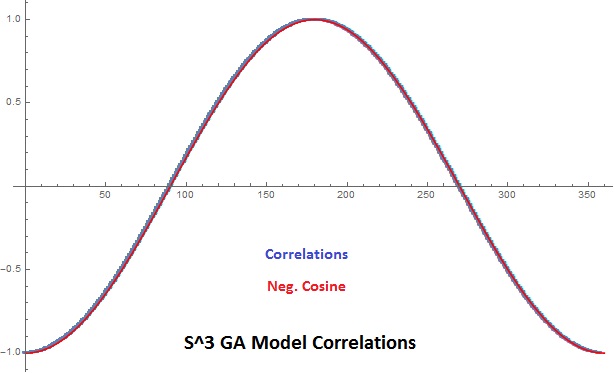
And the result is for 50,000 trials with random angles at one degree resolution and plotting the data in Mathematica,
.

