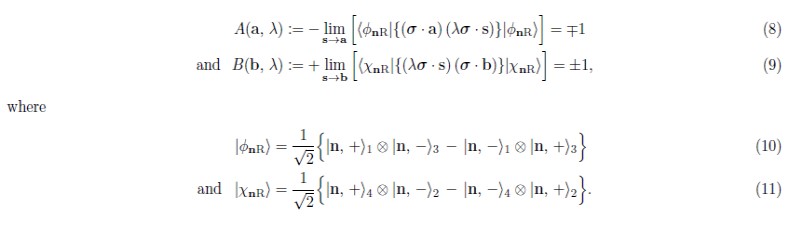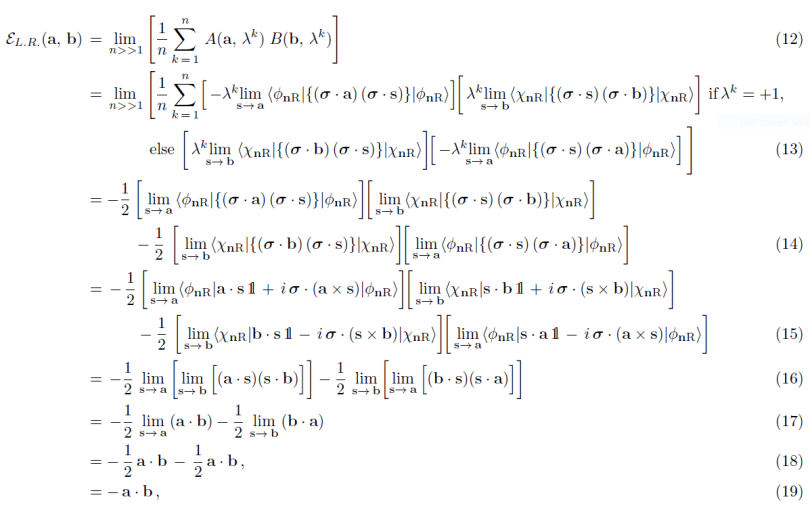SciPhysicsForums.com

Hi Folks,

We know you all have been waiting for this one so here it is.

download/QM_with_HV_is_Local_draftv2.pdf

Quantum mechanics with Joy Christian's hidden variable is local!

Enjoy!
.

And here are the manifestly local measurement functions for A and B.

Excellent! It is so good to disentangle Joy Christian's basic idea from Geometric Algebra, beautiful and important though that may be. I think I see the same issues in this computation as I had earlier. I will let the authors know privately, via Jay.

gill1109 wrote:Excellent! It is so good to disentangle Joy Christian's basic idea from Geometric Algebra, beautiful and important though that may be. I think I see the same issues in this computation as I had earlier. I will let the authors know privately, via Jay.

Sorry to chase away your "passion at a distance" but it is gone for good now. No more spooky junk to deal with. Joy was right after all.

FrediFizzx wrote:
And here are the manifestly local measurement functions for A and B.

The derivation of the local-realistic correlation between the above two measurement functions is quite similar to that in my original 3-sphere model: https://arxiv.org/pdf/1103.1879.pdf.

This is not surprising, because the derivation makes use of the Pauli Identity [equation (5) of this paper], which is isomorphic to the bivector subalgebra of the Clifford algebra Cl(3,0), and bivector subalgebra is precisely what defines a quaternionic 3-sphere. As a result, much of the rationale behind the derivation below is the same as that in my 3-sphere model linked above.


***

It is anyway good to conclude that no knowledge of Geometric Algebra is needed to follow this paper, since that has always been an obstacle for the dissemination and evaluation of your theory.

If you want to convince the physics society that HV local model can be sufficient (I personally agree but using 4D local like in action optimizing), for exercise start with showing how (like QM) it can violate the most obvious inequality:
Pr(A=B) + Pr(A=C) + Pr(B=C) >= 1
that flipping 3 coins, at least two are equal.
Its obviousness and simplicity does not allow for some magical interpretation, handwaving ...

Jarek wrote:If you want to convince the physics society that HV local model can be sufficient (I personally agree but using 4D local like in action optimizing), for exercise start with showing how (like QM) it can violate the most obvious inequality:
Pr(A=B) + Pr(A=C) + Pr(B=C) >= 1
that flipping 3 coins, at least two are equal.
Its obviousness and simplicity does not allow for some magical interpretation, handwaving ...

We already know that it exceeds the Bell bounds. -a.b is our result.

Could you elaborate?
This is much less sophisticated inequality than e.g. CHSH, directly obvious.
You need a local HV model which gets below 1, just try to understand its difficulty.

Jarek wrote:Could you elaborate?
This is much less sophisticated inequality than e.g. CHSH, directly obvious.
You need a local HV model which gets below 1, just try to understand its difficulty.

There is no difficulty. "This inequality", or Bell-CHSH inequality, or any other inequality you dream up with, has nothing to do with the physics of how the actual experiments are done.

The physical question -- and the only question that matters physically -- is whether or not a local-realistic model can reproduce the strong correlation -a.b. The answer is: Yes, it can.

***

Looking at abstract, you are attacking assumptions in derivation of more sophisticated inequalities.

Pr(A=B) + Pr(A=C) + Pr(B=C) >= 1 does not use any sophisticated assumptions, just "flipping 3 coins at least 2 are equal",
or better:
choose any probability distribution among 8 possibilities Pr(ABC) >= 0, sum_ABC Pr(ABC) = 1
Pr(A=B) = Pr(000) + Pr(001) + Pr(110) + Pr(111)
Pr(A=C) = Pr(000) + Pr(010) + Pr(101) + Pr(111)
Pr(B=C) = Pr(000) + Pr(100) + Pr(011) + Pr(111)
summing all three and using sum_ABC Pr(ABC) = 1:
Pr(A=B) + Pr(A=C) + Pr(B=C) = 1 + 2Pr(000) + 2Pr(111) >= 1
Please point unjustified assumptions in this derivation, or show construction allowing to get Pr(A=B) + Pr(A=C) + Pr(B=C) < 1.

Personally, I see the problematic assumption in "probability of union of disjoint events is sum of their probabilities": pAB? = pAB0 + pAB1, leading to above inequality.
In contrast, in QM we can operate using Born rule instead: "probability of union of disjoint events is proportional to square of sum of their amplitudes": pAB? ~ (psiAB0 + psiAB1)^2, what allows to violate such inequalities.
The question is how to get local HV models with Born rule?

***
As I noted above, all inequalities are red herring. They are a worthless distraction from the actual physics and from what can be observed in the actual experiments.

The only physical question of interest in the Einstein-Bell debate is this: Given a pair of measurement functions A(a, h) and B(b, h) defined by Bell, where a and b are freely chosen experimental parameters and h is a shared randomness between Alice and Bob, can the average of their product equal to -a.b? In other words, can the following equality hold?

E(a, b) = 1/n Sum_k A(a, h_k) B(b, h_k) = -a.b

The answer is: Yes, it can. And the paper being discussed in this thread demonstrates how. A purely geometrical version of the model can be found here: https://arxiv.org/abs/1103.1879.

***

We don't have products in the inequality I am asking for, just sums: "probability of alternative of disjoint events is sum of their probabilities" - how would you apply your argument here?

ps. Pictorial proofs in Maccone's paper: https://arxiv.org/pdf/1212.5214.pdf

Jarek wrote:We don't have products in the inequality I am asking for, just sums: "probability of alternative of disjoint events is sum of their probabilities" - how would you apply your argument here?

ps. Pictorial proofs in Maccone's paper: https://arxiv.org/pdf/1212.5214.pdf

As I said before, what you are asking has nothing whatsoever to do with physics or the EPRB experiments. You are asking questions that have no relevance for what this thread is about.

***

Heinera wrote:It is anyway good to conclude that no knowledge of Geometric Algebra is needed to follow this paper, since that has always been an obstacle for the dissemination and evaluation of your theory.

I don't know why. Geometric Algebra is pretty easy to learn. You can learn the basics in less than a day and it is a really powerful mathematical tool. Anyways, looking forward to your comments about the paper.

FrediFizzx wrote:

Heinera wrote:It is anyway good to conclude that no knowledge of Geometric Algebra is needed to follow this paper, since that has always been an obstacle for the dissemination and evaluation of your theory.

I don't know why. Geometric Algebra is pretty easy to learn. You can learn the basics in less than a day and it is a really powerful mathematical tool. Anyways, looking forward to your comments about the paper.

Perhaps it was not the Geometric Algebra (GA) so much as a difficulty but the 3-sphere topology. That is more difficult to grasp. But as Joy alludes to above, S^3 exists in the quantum model also. It is just more easy to describe using GA than trying to use the probabilistic math of QM.

Joy Christian wrote:The physical question -- and the only question that matters physically -- is whether or not a local-realistic model can reproduce the strong correlation -a.b.
***

Joy's statement above, specifically in reference to a spin 0 singlet prepared state and local hidden variables, is 100% correct. IF a local realistic hidden variables model can properly reproduce this correlation, then that theory would necessarily go outside the classical bounds of any "inequalities" one might conjure up, and Bell's Theorem would become history.

The "IF" I put in the previous sentence, is the main question we are discussing. And what I am focused on at present is not just any old model, but quantum mechanics itself, and whether QM, properly developed and understood, might in fact itself come to be seen as a local, realistic, and complete hidden variables theory.

Jay

FrediFizzx wrote:And here are the manifestly local measurement functions for A and B.

For given values of a and , the RHS of (8) and (9) looks completely deterministic to me. Where is the extra source of randomness that can produce both +1 and -1 for the same values of a and ?

Heinera wrote:

FrediFizzx wrote:And here are the manifestly local measurement functions for A and B.

For given values of a and , the RHS of (8) and (9) looks completely deterministic to me. Where is the extra source of randomness that can produce both +1 and -1 for the same values of a and ?

You were right that extra randomness. We took that out because it can give AB = +1 instead of AB = -1 when a = b.

Heinera wrote:For given values of a and , the RHS of (8) and (9) looks completely deterministic to me. Where is the extra source of randomness that can produce both +1 and -1 for the same values of a and ?

This is a quantum mechanical version of the 3-sphere model. Theerefore "the extra source of randomness that can produce both +1 and -1 for the same values of a and " comes from the geometry of the 3-sphere. See my previous post about this question: viewtopic.php?f=6&t=385#p8843.

***