If we are going to make any progress in understanding this Bell mess, we have to be more precise and less hand-wavy in our discussions. Most often, words are selected to describe concepts that don't really fit the word, then people object to specific words based on their own limited understanding of what the word might mean without a careful understanding of what really is being talked about. "Superdeterminism" is one of the culprits/scapegoats but it really is not more/less scientific than any of the other words associated with Bell such as "non-locality", "non-realism", etc.
For the EPRB experiment we have three "correlation" quantities.
 = \int_{\Lambda} A(a,\lambda )B(b,\lambda ) \rho (\lambda ) d\lambda)
 = \int_{Z} A(b,\zeta )B(c,\zeta ) \rho (\zeta ) d\zeta)
 = \int_{\Xi} A(b,\xi )B(c,\xi ) \rho (\xi ) d\xi)
From which Bell derives an inequality
 - P(b, a) - P(b, c) \le 1)
Relying on the assumption that
.
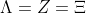
Experimentally, for the purposes of comparing with the inequality, we can measure
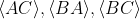
for which we implicitly assume that
 \approx \langle AC\rangle, P(b, a) \approx \langle BA \rangle, P(b, c) \approx \langle BC \rangle)
for a large enough number of measurements. Since measurements are always countable, we have
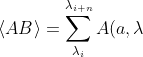B(b,\lambda );\ \Lambda_{AB} = {\lambda_i, .., \lambda_{i+n}})
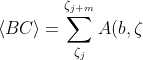B(c,\zeta );\ Z_{BC} = {\zeta_j, .., \zeta_{j+m}})
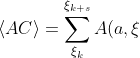B(c,\xi );\ \Xi_{AC} = {\xi_k, .., \xi_{k+s}})
Where,
, and therefore, not only do we carry forward Bell's assumption that
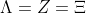
, we now have a distinct an even stronger assumption that
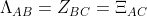
, since it is possible and likely for
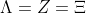
to be true and
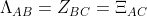
to be false. Experimentally,
are disjoint but even if the sets are not exactly the same, probability distributions may be so similar that you should still have
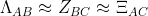
and thus obtain almost the same expectation values as if they were equal.
Realism is the idea that three ensembles originate from the same sample space implying that
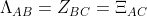
. Experimentally, the only way an experimenter can enforce this, is to measure the three averages
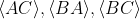
simultaneously on the same set of particle pairs -- a practical impossibility. Note that this understanding of realism, does not translate to mystical notions of the moon not being there when nobody is looking, or fanciful notions of whether particles have properties before measurement. Also, note that, it is abject stupidity to claim to have ruled out realism on the basis of Bell's theorem, if you did not perform all your measurements on the same set of particle pairs at the same time.
Locality is the idea that Bell's outcome functions A(., .), and B(.,.) generate the the outcomes based only on inputs from within the light-cone of each experimental station. Imagine a process producing the ensembles
 \neq Z_{BC}(b,c) \neq \Xi_{AC}(a,c))
.
These ensembles are now dependent on the settings, thus effectively converting Bell's outcome functions from
))
to
)
. This is the form most commonly associated with non-locality. By placing the stations far apart and carefully timing the measurements, the only way for Alice's setting to influence Bob's outcome is by non-local transmission of the setting to the other side. It begs the question then, why can't we transmit information this way? Anyway, the main result is that the ensembles are different, contrary to Bell's key assumption. "Backward-causation", "instantaneous" communication, and "non-locality" are slight variations of the same thing.
Contextuality is not very different from the locality case either. Except we now have the ensembles:
 \neq Z_{BC}(prep_{BC}) \neq \Xi_{AC}(prep_{AC}))
.
Which is saying, in order to measure those outcomes, we need three distinct and incompatible experimental preparations (contexts), and therefore we end up with ensembles that are necessarily different. Isn't this in fact what is done in EPRB experiments? Note that
preparation involves not just the things you do before the experiment, but must include everything, including setup and post-selection of the data used directly in calculating the averages. Therefore, the mere act of selecting subsets of data based on what settings were used on both sides, makes the resulting post-selected data statistically dependent on the settings on both sides. Hess, De Raedt, Accardi and others argue that when measuring on different sets of particles at different times, it is natural to expect differences in context that are angle dependent.
Superdeterminism is the idea that Alice and Bob, when performing an EPRB experiment do not have the freedom to make
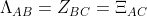
. In other words, it is impossible to eliminate the statistical dependence between
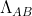
and
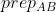
, etc that result in different ensembles. Note that superdeterminism says nothing about the experimenter's free-will to pick specific settings at specific times. It simply says, no matter what they can do freely, don't have the freedom to make the ensembles statistically independent of the context.
To conclude, note that everything centers whether the ensembles are the same or not. Even loopholes are mechanisms for introducing context-dependent (settings dependent) differences between the ensembles. For example
detection loophole: some particle pairs are less likely to be detected at certain angles than others;
coincidence loophole: the likelihood of matching a pair varies with angle difference.
This is why I think some key aspects of this article (
https://doi.org/10.1103/PhysRevA.57.3304) have been overlooked even by the authors themselves.
Posted: Mon Jul 29, 2019 3:43 am
. Unfortunately, you've been asking the wrong questions. The issue is not which loophole was closed in what experiment, but what mechanisms are present in the experiment to ensure that the ensembles would be the same. Simply generating settings randomly is not sufficient, as the settings do not generate the outcomes all by themselves. (see this thread