Joy Christian wrote:… It is the same thing. Bell's local model of 1964 he is referring to in the above paragraph predicts individual A and B outcomes event-by-event. About ten years ago someone simulated its nonlocal version for me to convince me that only nonlocal models can reproduce the -a.b correlations, and rather easily. I continued working on my 3-sphere model regardless.
***
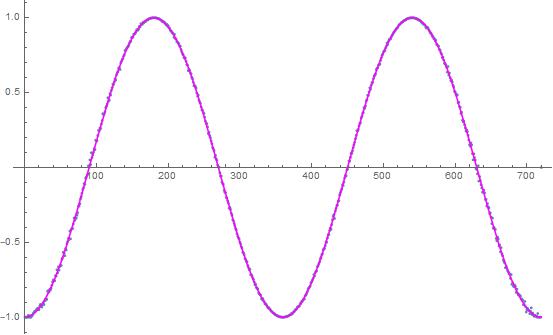
It looks like to me that with Bell's configuration, you will get straight lines event by event instead of the negative cosine curve. Bell's HV is just the particle spin vector. You need this function,
\right),B=A,B=-A\right];)
with lambda random 0 to 1 to produce the negative cosine curve. But it is complete nonsense anyways. Not only does station B know A's angle, it also knows A's outcome. Very un-Natural.
.