Simulation with non-local behavior
Looks like it might be possible to predict individual outcomes event by event with grossly non-local behavior. It is a non-local hidden variable model with 720 degrees of data at 1 degree resolution.
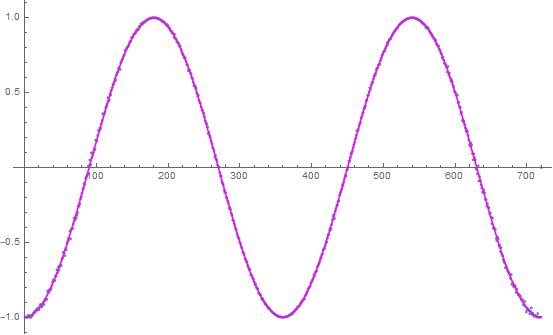
Here is a PDF of the Mathematica simulation,
EPRsims/non-local.pdf
The only problem with this is that output A is a coin toss variable. So you have to know a, b, lambda and A to predict the correct outcome for B. Don't know if this actually relates to quantum mechanics in any way.
.

Here is a PDF of the Mathematica simulation,
EPRsims/non-local.pdf
The only problem with this is that output A is a coin toss variable. So you have to know a, b, lambda and A to predict the correct outcome for B. Don't know if this actually relates to quantum mechanics in any way.
.
