gill1109 wrote:Gordon Watson wrote:gill1109 wrote:Gordon Watson wrote:For Richard Gill and other Bellians:
CHSH-Bell refuted via high-school math.
A brief draft: To be included as Appendix II when
https://vixra.org/pdf/2011.0073v1.pdf -- Watson 2020M.v1 -- is revised. E&OE.
6. Appendix IIVia
http://cds.cern.ch/record/400330/files/CM-P00058691.pdf, eqn (4.5), we have:
The
CHSH-Bell inequality:
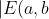-E(a,d)|+|E(b,c)+E(c,d)|\leq2.)
(1)
However, from my (32); say
WI-1:
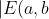-E(a,d)|\leq1-E(a,b)E(a,d).)
(2)
Similary:
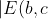+E(c,d)|\leq1+E(b,c)E(c,d).)
(3)
Therefore, inserting (2) and (3) into LHS (1), we have:
WI-2:
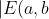-E(a,d)|+|E(b,c)+E(c,d)|\leq2-E(a,b)E(a,d)+E(b,c)E(c,d).)
(4)
So
WI-1 refutes Bell's inequality,
BI, 1964:(15). And
WI-2 refutes the
CHSH-Bell inequality.
Note, consistent with TLR: the results here require no assumptions beyond Bell's (1964) equations (1), LHS (2) with RHS (3). And high-school math.
Contrarily:
CHSH-Bell is based on four occasions where the pairwise-binding of EPRB observables is missed or ignored.
QED.
.
Why do you say there’s a contradiction? And where’s the justification of (2 and (3)? I don’t like (1) because it’s too complicated. I think it’s wrong. I prefer something one can develop some feeling for like r(11) </= 2 + r(12) + r(22) + r(21) where r(ab) stands for the correlation when Alice uses her setting number "a" and Bib uses his setting number "b". By flipping the sign of one or the other of the party's outcomes, by exchanging Alice's "1" and "2", and independently exchanging Bob's "1" and "2", and exchanging Alice for Bob, one obtains exactly 8 distinct one-sided CHSH inequalities. See Fine (1982). Together with 4 no-signalling equalities, necessary and sufficient for a local realist model for the 16 probabilities p(xy|ab).
Where do I say there's a contradiction? Are you comparing my (4) with Bell's effort, as documented in (1)? That's a refutation. The one (mine) never false, the other (being Bellian) often so. Why not test both with your favored angles?
The justification for (2) is (32) from the draft
https://vixra.org/pdf/2011.0073v1.pdf that I linked to.
Let's see if you can get to (3)
similarly, as I wrote.
I asked you to nominate your favoured Bell-inequality and the related angles that best illustrate the point you want to make. You did not. So I went for CHSH-Bell, see Bell's book (1987:35) that you alluded to. NOW you say you "don’t like (1) because it’s too complicated. You think it’s wrong." Too complicated for you: OK. But it's a famous Bellian inequality, so of course it's wrong. That's why I refute and correct it with high-school math.
Incidentally, I have not found you alleged critique of my similar "high-school" refutation of Bell's famous 1964:(15). I asked your for help to find it. Does it exist?
The rest of your comment seems panicked and irrelevant. Let's deal with the facts at hand:
Using nothing but Bell's 1964:(1) and high-school math, I refute the two most famous Bellian inequalities.
[I then use (though I've not carried on and done that here) Bell's (1964) equations, LHS (2) with RHS (3), to show that my inequalities are never false. Because, of course, unlike Bell: my results are consistent with QM.]
PS: Since you offer no critique of my "high-school" math here, please provide such, or point me to it elsewhere. You did imply that the critique was in this thread. Right?
Thanks.
.
Gordon, you derive some inequalities which are always true. Bell derived an inequality under certain special assumptions. His inequality is violated by some quantum mechanical predictions. Bell’s conclusion is that the assumptions he made in order to derive his inequalities must be false. You agree with him. You called his assumptions “naïeve”. Niels Bohr would have agreed with you, as Bell himself pointed out.
I don’t like the version of CHSH with absolute values. |x| has to be read as “x if x > 0 and otherwise -x”. The form I give the inequalities - as a collection of 8 simple intuitive one-sided inequalities - is cleaner, it’s equivalent, it’s more powerful (necessary and sufficient conditions), it goes back to Boole’s N&SC in his magnum opus (the foundation of Boolean logic and elementary probability theory). It generalises to the case of experiments with more settings, more parties, more outcomes. The local polytope.
https://arxiv.org/abs/1207.5103. Generalised Bell inequalities.
TOWARD SOME PRELIMINARY CLARIFICATIONS IN RELATION TO BELL AND GILL (2014):
(1) What statement (with source) does Bohr make that agrees with my position (as seen by you)?
(2) What statement did Bell make about Bohr's statement; ie, what did Bell point out?
(3) In Gill (2014:1) you say that "Bell's theorem should lead us to relinquish realism." What definition and implications of "realism" are you relying upon here? Please be expansive so that I might understand remarks like those on p.3 of your 2014.
(4) I expect to have quite a bit to say about your 2014. Are there any points there that you no longer maintain?
(5) Does Bell give any reasons for not relinquishing this "realism"?
(6) I ask because, in the following statements (per my draft, first page) from 1990 and 1964, Bell makes no mention of realism:
After Bell (1990):p.5: ‘I cannot say that action at a distance (AAD is required in physics. But I can say that you cannot get way with no AAD. You cannot separate off what happens in one place and what happens in another. Somehow they have to be described and explained jointly.’ p.6: ‘The Einstein program fails, that’s too bad for Einstein, but should we worry about that? So what? ... it might be that we have to learn to accept not so much AAD, but the inadequacy of no AAD.’ p.7: ‘And that is the dilemma. We are led by analysing this situation to admit that in somehow distant things are connected, or at least not disconnected. ... So the connections have to be very subtle, and I have told you all that I know about them.’ p.9: ‘It’s my feeling that all this AAD and no AAD business will go the same way [as the ether]. But someone will come up with the answer, with a reasonable way of looking at these things. If we are lucky it will be to some big new development like the theory of relativity. Maybe someone will just point out that we were being rather silly, and it won’t lead to a big new development. But anyway, I believe the questions will be resolved.’ p.10: ‘I think somebody will find a way of saying that [relativity and QM] are compatible. For me it’s very hard to put them together, but I think somebody will put them together, and we’ll just see that my imagination was too limited.’ p.12: ‘I don’t know any conception of locality that works with QM. So I think we’re stuck with nonlocality.’ p.13: ‘... I step back from asserting that there is AAD, and I say only that you cannot get away with locality. You cannot explain things by events in their neighbourhood. But I am careful not to assert that there is AAD.’
Bell (1964):‘In a theory in which parameters are added to quantum mechanics to determine the results of individual measurements, without changing the statistical predictions, there must be a mechanism whereby the setting of one measuring device can influence the reading of another instrument, however remote. Moreover, the signal involved must propagate instantaneously, so that such a theory could not be Lorentz invariant.’
(7) So, seeking to be very clear:
why would Bell hold these views AGAINST the "realism" that you have yet to clarify for me?
PS: As Bell half-expected, true local realism (TLR) solves or revolves all of Bell's difficulties.
EDIT: I do not recall saying that
Bell's assumptions are “naïeve”. I defined
true realism (or
non-naive realism): some existents change interactively.
.
.

