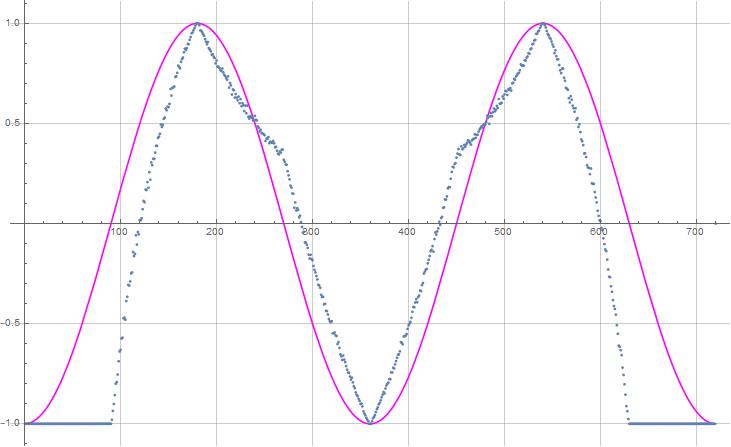
Quaternion simulation no hidden variable
Ok folks, are you ready for yet another simulation that shoots down Bell's theory? Of course you are.  I've modified and enhanced John Reed's original Mathematica quaternion simulation to use full 3D vectors and no hidden variable that follows the GAViewer simulation here. The quaternions actually work better for the production calculation. Here is a PDF file of the Mathematica simulation,
I've modified and enhanced John Reed's original Mathematica quaternion simulation to use full 3D vectors and no hidden variable that follows the GAViewer simulation here. The quaternions actually work better for the production calculation. Here is a PDF file of the Mathematica simulation,
EPRsims/prod_calc_quat2.pdf
Here is the notebook file,
EPRsims/prod_calc_quat2.nb
Of course the product calculation is exactly -a.b,
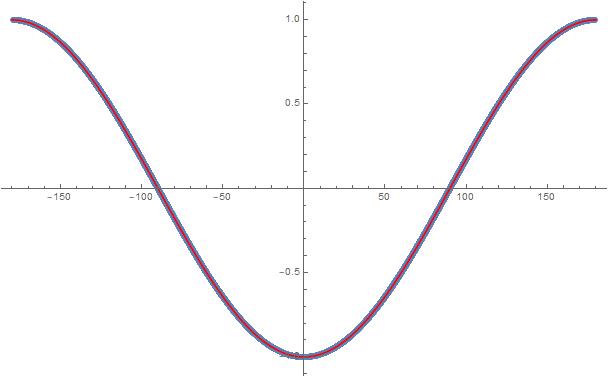
The blue is the product calculation data points and the red is the negative cosine curve. So, we have yet another completely local model that is a counter example to Bell's junk physics theory! Bam!
.
EPRsims/prod_calc_quat2.pdf
Here is the notebook file,
EPRsims/prod_calc_quat2.nb
Of course the product calculation is exactly -a.b,

The blue is the product calculation data points and the red is the negative cosine curve. So, we have yet another completely local model that is a counter example to Bell's junk physics theory! Bam!
.