Hi Jay,
I am indeed making use of orientation entanglement in my explanation of the EPR correlation. Orientation entanglement is also responsible for the exclusion principle. So we are indeed talking about "double covering", SU(2), and all that. So we are on the same page as far as the orientation entanglement is concerned. I often use the phrase "parallelized 3-sphere" which may not be too familiar, but that is just a matter of language. Ultimately this is all about the significance of the SU(2) symmetry.
But the relationship between the orientation entanglement and quantum entanglement is not so straightforward. To begin with, quantum entanglement is a
quantum concept, involving superposition principle and non-factorizability. Thus it is dramatically different from the classical concept like the orientation entanglement. Let me elaborate on this a little because it is important to appreciate just how profoundly different the concept of quantum entanglement is. Consider the simplest entangled state---i.e., the singlet state:
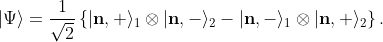
This state
cannot be factorized into a product of a state representing the first spin alone and a state representing the second spin alone, such as (for example)
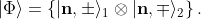
Because of this non-factorizability the singlet state is said to be
entangled. And this entanglement is responsible for the so-called non-locality of quantum theory. Note that this entanglement is a purely quantum mechanical concept. It has nothing whatsoever to do with the classical concept of orientation entanglement. In particular, it has nothing to do with internal symmetry or spacetime. Quantum entanglement can be between energy and momentum of a particle, for example.
Why do I then claim that at the root of it all is orientation entanglement and not quantum entanglement? Was Schrodinger wrong to call quantum entanglement
the characteristic trait of quantum mechanics? No, he wasn't wrong. Quantum entanglement is indeed a powerful, succinct, and phenomenally successful concept. But unlike orientation entanglement, one
cannot observe either quantum superposition or quantum entanglement directly. In this respect quantum entanglement is no different from the idea of a phlogiston in a combustible body. Recall that
phlogiston theory was a very successful and powerful theory which remained popular in accounting for the actually observed phenomena, such as burning wood producing ash lighter than wood. But phlogiston itself was merely a hypothetical substance which could not be observed directly. Conceptually quantum entanglement is no different. It can never be observed directly (although time and again some people falsely claim that they have "observed" quantum entanglement itself

). If we could observe quantum entanglement directly, then all controversies over the interpretation of quantum mechanics would end instantly. Then Einstein and the followers of Einstein like you and me would have no choice but to concede defeat.
What we
can observe directly are probabilities, expectation values, and correlations among observed results. Those are the "realities", not quantum entanglement. This is markedly different from orientation entanglement, which is itself a "reality" (cf. Dirac's belt trick). Given a self-adjoint operator, say
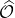
, representing some observable quantity, the expectation value of this operator in an entangled state,

, provides the predictions of what we observe in any physical scenario. What I have found in my work is that this expectation value, which is closely related to correlation among the observed results like +1 or -1, can be understood local-realistically as correlation among the points of the mathematical space, namely the 3-sphere, representing all possible orientation entanglement in three dimensions.
This immediately raises the question of generalization you have raised: "...might you not be able to generalize that to take all the mystery out of quantum entanglement as well?". Well, I think I have indeed taken all the mystery out of quantum entanglement. But to understand how, one has to understand the octonionic spinors and the corresponding parallelized 7-sphere. I have already given the general argument in another thread, but let me repeat it here for completeness:
Suppose we consider an arbitrary quantum state
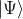
and the corresponding self-adjoint operator
)
in some Hilbert space
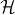
, parameterized by an arbitrary number of
local parameters
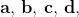
etc. Note that I am imposing no restrictions on the state
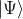
, or on the size of the Hilbert space
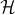
. In particular,
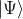
can be as entangled or un-entangled as one may like, and
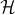
can be as large or small as one may like (in the case of the double slit there is no entanglement, for example). The quantum mechanical expectation value of the operator
)
in the state
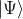
would then be
\, =\,\text{Tr}\left\{{W}\,{\cal\widehat O}({\bf a},\,{\bf b},\,{\bf c},\,{\bf d},\,\dots\,)\right\})
,
where
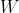
is a statistical operator of unit trace representing the state. Now I have shown that the quantum correlation predicted by this expectation value can always be reproduced as local and realistic correlation among a set of points of a parallelized 7-sphere, by following a procedure very similar to the one discussed above for the 3-sphere, which is simply one of the Hopf fibers of the 7-sphere. In fact, I have proved the following theorem:
Every quantum mechanical correlation can be understood as a deterministic, local-realistic correlation among a set of points of a parallelized 7-sphere, specified by maps of the form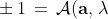: {\rm I\!R}^3\!\times\Lambda\longrightarrow {\rm I\!R}^7\!\times\Lambda\longrightarrow S^7 \hookrightarrow{\rm I\!R}^8)
.
The proof of this theorem can be found in
this paper. I think you will not find this satisfactory because you would like to have intuitive, physical understating of what is going on. But that could be a dangerous undertaking. Without understanding the intricacies of the octonionic 7-sphere, it could lead to serious misconceptions.
Joy

