Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
97 posts
• Page 3 of 5 • 1, 2, 3, 4, 5
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
Cool! Thank you for the link and info. Will read both tomorrow with great interest.
- local
- Posts: 295
- Joined: Mon Aug 05, 2019 1:19 pm
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
Here is some typical output of the GAViewer code that is in the paper.
One can see that the correlation matches up perfectly to neg_adotb event by event so verifies the product calculation. And that the bivectors are vanishing in the "mean".
.
- Code: Select all
neg_adotb = 0.574949
theta = 234.903931
correlation = 0.574949
neg_adotb = 0.386546
theta = 247.260223
correlation = 0.386546
neg_adotb = 0.006321
theta = 90.362167
correlation = 0.006321
neg_adotb = -0.487911
theta = 60.796616
correlation = -0.487911
neg_adotb = 0.196614
theta = 101.339050
correlation = 0.196614
neg_adotb = -0.526722
theta = 58.215748
correlation = -0.526722
neg_adotb = 0.898704
theta = 153.988235
correlation = 0.898704
neg_adotb = -0.832386
theta = 33.655334
correlation = -0.832386
neg_adotb = 0.113726
theta = 96.530151
correlation = 0.113726
neg_adotb = 0.461435
theta = 242.520279
correlation = 0.461435
neg_adotb = 0.399192
theta = 246.472336
correlation = 0.399192
neg_adotb = 0.532410
theta = 122.168465
correlation = 0.532410
neg_adotb = -0.392552
theta = 66.886620
correlation = -0.392552
neg_adotb = 0.254378
theta = 104.736710
correlation = 0.254378
mean = 0.001660 + 0.004355*e2^e3 + -0.001763*e3^e1 + -0.002109*e1^e2
aveA = 0.004108
aveB = 0.000323
One can see that the correlation matches up perfectly to neg_adotb event by event so verifies the product calculation. And that the bivectors are vanishing in the "mean".
.
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
Happy Thanksgiving to all!
And thank you FrediFizzx for the great forum.
And thank you FrediFizzx for the great forum.
- local
- Posts: 295
- Joined: Mon Aug 05, 2019 1:19 pm
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
local wrote:Happy Thanksgiving to all!
And thank you FrediFizzx for the great forum.
You're welcome and Happy Thanksgiving to you and all.
Now, if I could just figure out the function for the
.
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
Joy Christian wrote:***
Ok., here is the new paper: https://arxiv.org/abs/1911.11578.Title: Dr. Bertlmann's Socks in the Quaternionic World of Ambidextral Reality
Abstract:
In this pedagogical paper, John S. Bell's amusing example of Dr. Bertlmann's socks is reconsidered, first within a toy model of a two-dimensional one-sided world of a non-orientable Möbius strip, and then within a real world of three-dimensional quaternionic sphere, S^3, which results from an addition of a single point to R^3 at infinity. In the quaternionic world, which happens to be the spatial part of a solution of Einstein's field equations of general relativity, the singlet correlations between a pair of entangled fermions can be understood as classically as those between Dr. Bertlmann's colorful socks.
I have revised the pedagogical paper: https://arxiv.org/abs/1911.11578.
I have added an appendix proving the equivalence of the conservation of spin angular momentum and the twists in the Hopf bundle of S^3. This makes the paper more technical than I intended it to be, but the technicality (as beautiful as it is) is in the appendix and can be ignored in the first reading.
I have also added a couple of explanatory lines in the code presented in Section IV to bring the code more in line with the analytical derivation of the singlet correlations.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
***
Quite independently of any cosmological model, for the past twelve years I have argued for a closed S^3 model for the 3D physical space. My argument comes from a local-realistic understanding of quantum correlations. It is good to know that cosmological data also now seem to support the closed model for the physical space:
"... the Planck cosmic microwave background spectra now preferring a positive curvature at more than 99% confidence level":
https://www.nature.com/articles/s41550-019-0906-9
***
Quite independently of any cosmological model, for the past twelve years I have argued for a closed S^3 model for the 3D physical space. My argument comes from a local-realistic understanding of quantum correlations. It is good to know that cosmological data also now seem to support the closed model for the physical space:
"... the Planck cosmic microwave background spectra now preferring a positive curvature at more than 99% confidence level":
https://www.nature.com/articles/s41550-019-0906-9
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
***
Happy New Year to everyone!
I have revised my pedagogical paper once again: https://arxiv.org/abs/1911.11578. The last couple of lines of the following paragraph, including Eq. (40), are new in this version:

Nota bene: If a null vector is like the teeth of the Cheshire Cat, then a null bivector is like the grin of the Cheshire Cat, with the Cat itself being the vector or the bivector, respectively.

But seriously, just as a null vector is a vector that has no length (or has vanishing magnitude) and no direction, a null bivector is a bivector that spans no area (or spans zero area) and has no direction. Moreover, in Geometric Algebra there is only one notion of zero for elements of all grades. In other words, there is only one notion of zero for the scalars, vectors, bivectors, trivectors, and multivectors, not separate notions of zero for each grade or a composite of grades.
More importantly, I claim that my pedagogical paper provides the best explanation to date of the observed strong correlations in strictly local, realistic, and deterministic terms.
***
Happy New Year to everyone!
I have revised my pedagogical paper once again: https://arxiv.org/abs/1911.11578. The last couple of lines of the following paragraph, including Eq. (40), are new in this version:

Nota bene: If a null vector is like the teeth of the Cheshire Cat, then a null bivector is like the grin of the Cheshire Cat, with the Cat itself being the vector or the bivector, respectively.

But seriously, just as a null vector is a vector that has no length (or has vanishing magnitude) and no direction, a null bivector is a bivector that spans no area (or spans zero area) and has no direction. Moreover, in Geometric Algebra there is only one notion of zero for elements of all grades. In other words, there is only one notion of zero for the scalars, vectors, bivectors, trivectors, and multivectors, not separate notions of zero for each grade or a composite of grades.
More importantly, I claim that my pedagogical paper provides the best explanation to date of the observed strong correlations in strictly local, realistic, and deterministic terms.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
***
I have revised my pedagogical paper once again to make the above comments regarding the disappearing Cheshire Cat more transparent (Reference: Alice's Adventures in Wonderland).
The revised part of the paper is a new paragraph that includes equations (54) to (62). In fact, let me reproduce the new derivation of the strong correlations to show how beautiful it is. What is calculated in the derivation of the expectation value E(a, b) below is correlations between the limiting scalar points, A = +/-1 and B = +/-1, of a quaternionic 3-sphere (i.e. S^3):
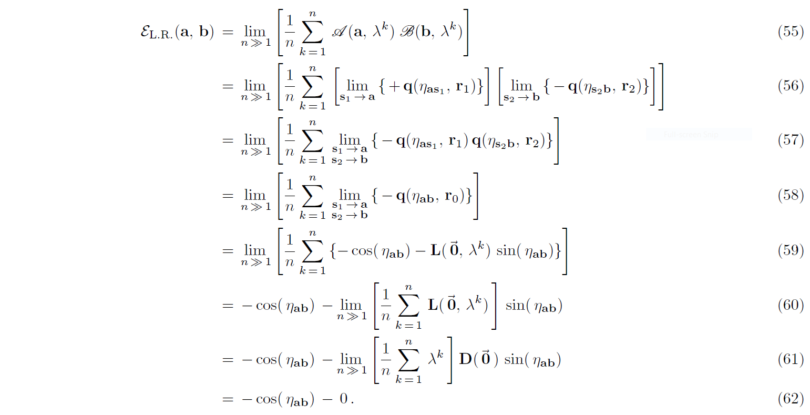
A line-by-line explanation of this derivation is given in the paragraph that includes it. There are two differences between this derivation and all of the previous derivations of the strong correlations I have presented. While all derivations are based on imposing the law of conservation of spin angular momentum by setting s1 = s2, in this derivation the two limits s1 --> a and s2 --> b are actually carried out rather than made superfluous. The consequence is that we end up with a null bivector in eq. (59) instead of a bivector over the direction a x b. Thus the Cheshire Cat disappears already in eq. (59). Only its ghostly grin remains. But, as we can see from eqs. (59) to (62), even the cat's grin is wiped out in the end, thanks to the fact that handedness of the 3-sphere is necessarily a fair coin, which is the hidden variable in the model, and therefore it must be summed over in the calculation of the expectation value E(a, b).
***
I have revised my pedagogical paper once again to make the above comments regarding the disappearing Cheshire Cat more transparent (Reference: Alice's Adventures in Wonderland).
The revised part of the paper is a new paragraph that includes equations (54) to (62). In fact, let me reproduce the new derivation of the strong correlations to show how beautiful it is. What is calculated in the derivation of the expectation value E(a, b) below is correlations between the limiting scalar points, A = +/-1 and B = +/-1, of a quaternionic 3-sphere (i.e. S^3):
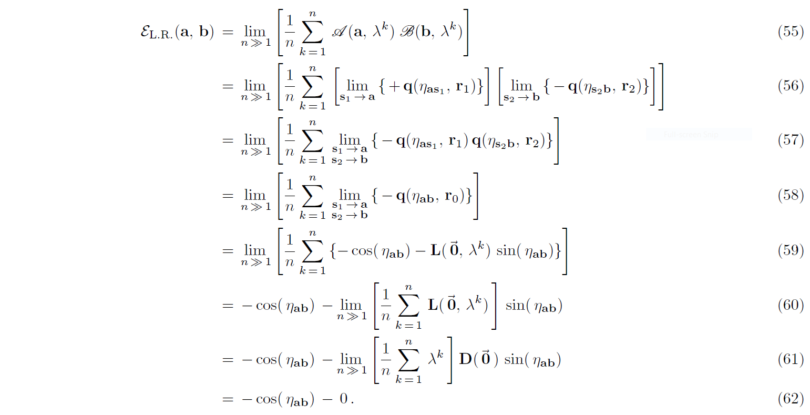
A line-by-line explanation of this derivation is given in the paragraph that includes it. There are two differences between this derivation and all of the previous derivations of the strong correlations I have presented. While all derivations are based on imposing the law of conservation of spin angular momentum by setting s1 = s2, in this derivation the two limits s1 --> a and s2 --> b are actually carried out rather than made superfluous. The consequence is that we end up with a null bivector in eq. (59) instead of a bivector over the direction a x b. Thus the Cheshire Cat disappears already in eq. (59). Only its ghostly grin remains. But, as we can see from eqs. (59) to (62), even the cat's grin is wiped out in the end, thanks to the fact that handedness of the 3-sphere is necessarily a fair coin, which is the hidden variable in the model, and therefore it must be summed over in the calculation of the expectation value E(a, b).
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
***
By the way, the entire second term in eq. (60) is a null bivector. And, just like a null vector, a null bivector is an additive identity. Therefore step (61) is not needed for the derivation of the strong correlation. In other words, eq. (60) is already equal to eq. (62). And with that, all the hullabaloo of a "sign error" by some unscrupulous critics of my work goes down the drain.
***
By the way, the entire second term in eq. (60) is a null bivector. And, just like a null vector, a null bivector is an additive identity. Therefore step (61) is not needed for the derivation of the strong correlation. In other words, eq. (60) is already equal to eq. (62). And with that, all the hullabaloo of a "sign error" by some unscrupulous critics of my work goes down the drain.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
Joy Christian wrote:
By the way, the entire second term in eq. (60) is a null bivector. And, just like a null vector, a null bivector is an additive identity. Therefore step (61) is not needed for the derivation of the strong correlation. In other words, eq. (60) is already equal to eq. (62). And with that, all the hullabaloo of a "sign error" by some unscrupulous critics of my work goes down the drain.
I have updated the paper on the arXiv to make the above point clear in the derivation. In the updated version 6, I have added the following two lines in the paragraph just below eq. (62):
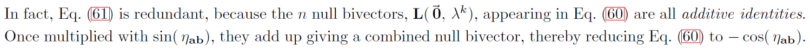
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
***
The story goes that Bertrand Russell, in a lecture on logic, mentioned that in the sense of material implication, a false proposition implies any proposition.
A student raised his hand and said: "In that case, given that 1 = 0, prove that you are the Pope."
Russell immediately replied:
"Add 1 to both sides of the equation: then we have 2 = 1. The set containing just me and the Pope has 2 members. But 2 = 1, so it has only 1 member; therefore, I am the Pope."
The moral of the story is that you can prove anything and claim anything about anything if you start out with an equation that is manifestly wrong in that its LHS is not equal to its RHS.
So don't forget to check your starting equation before making a fool of yourself.
Just saying.
***
The story goes that Bertrand Russell, in a lecture on logic, mentioned that in the sense of material implication, a false proposition implies any proposition.
A student raised his hand and said: "In that case, given that 1 = 0, prove that you are the Pope."
Russell immediately replied:
"Add 1 to both sides of the equation: then we have 2 = 1. The set containing just me and the Pope has 2 members. But 2 = 1, so it has only 1 member; therefore, I am the Pope."
The moral of the story is that you can prove anything and claim anything about anything if you start out with an equation that is manifestly wrong in that its LHS is not equal to its RHS.
So don't forget to check your starting equation before making a fool of yourself.
Just saying.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
***
I have revised my pedagogical paper again: https://arxiv.org/abs/1911.11578.
Among other minor edits, I have moved the simulation code to Appendix B and added the following new paragraph on page 7:

***
I have revised my pedagogical paper again: https://arxiv.org/abs/1911.11578.
Among other minor edits, I have moved the simulation code to Appendix B and added the following new paragraph on page 7:

***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
Joy Christian wrote:I have revised my pedagogical paper again: https://arxiv.org/abs/1911.11578.
Good to see you are active and making progress! Take care of yourself!
- gill1109
- Mathematical Statistician
- Posts: 2812
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: Leiden
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
gill1109 wrote:
Good to see you are active and making progress! Take care of yourself!
Thank you. And you too take care of yourself.
All I can do in the current situation is to think about physics. In the UK there have been over 5,000 confirmed cases of Covid-19 and 233 deaths already. Everything is closed except for the grocery stores. So all the viruses are now gathering in the grocery stores and I am apprehensive to go shopping. Not that there is anything available in the stores. All the shelves are empty. We have avoided Italy-style total lockdown so far. But we are only 14 days behind Italy and I expect things to get a lot worse in about two weeks. I am coping with the situation by thinking about physics and checking the news frequently. In 2020 we thought we would have flying cars, and here we are teaching everyone how to wash their hands.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
Joy Christian wrote:All I can do in the current situation is to think about physics.
Me too - well mathematics, not physics. You are very wise.
Actually I can talk to my colleagues - as long as internet still works - about stochastic epidemic models. There are interesting ideas coming up from physics: theory of "interacting particle systems". The network of connections in our populations is actually fractal and irregular (different parameters at different levels and in different locations...).
I'm lucky enough to live with a big town on one side and a big forest on the other side. I can still sneak into the forest from time to time, and get high on the oxygen levels there...
Lots of people are now doing amateur statistics. It's an ill wind which blows nobody any good, I suppose.
- gill1109
- Mathematical Statistician
- Posts: 2812
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: Leiden
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
***
Watch this space.
***
Watch this space.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
Joy Christian wrote:***
Watch this space.
My paper on Dr. Bertlmann's socks is now published online by IEEE Access: https://doi.org/10.1109/ACCESS.2020.3031734.
This is the third of my papers published this year. The first was a paper in pure mathematics, the second was in particle physics (in collaboration with Fred Diether), and now this one is on my old hobby-horse. It is about understanding quantum correlations in purely local, realistic, and deterministic terms --- i.e., in terms of Dr. Bertlmann's socks.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
Congratulations, Joy! Great to see the IEEE allowing all voices to be heard.
- local
- Posts: 295
- Joined: Mon Aug 05, 2019 1:19 pm
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
Yes this is wonderful! I agree, all voices must be heard. I will now submit my https://arxiv.org/abs/2001.11338 to the same journal.
Dr. Bertlmann's left- and right-handed socks
Richard D. Gill
I point out the Central error in the entertaining recent paper "Dr. Bertlmann's Socks in the Quaternionic World of Ambidextral Reality" by Joy Christian, arXiv:1911.11578v6
Dr. Bertlmann's left- and right-handed socks
Richard D. Gill
I point out the Central error in the entertaining recent paper "Dr. Bertlmann's Socks in the Quaternionic World of Ambidextral Reality" by Joy Christian, arXiv:1911.11578v6
- gill1109
- Mathematical Statistician
- Posts: 2812
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: Leiden
Re: Dr Bertlmann's socks and the 3-sphere model of EPR-Bohm
***
I have mentioned past criticisms of my work in Answer 1 of Question 1 of Appendix B of the paper, with appropriate citations to the criticisms and my responses to them.
All eighteen reviewers as well as the editors of IEEE Access were fully aware of the criticisms and my responses to them throughout the two rounds of the review process.
***
I have mentioned past criticisms of my work in Answer 1 of Question 1 of Appendix B of the paper, with appropriate citations to the criticisms and my responses to them.
All eighteen reviewers as well as the editors of IEEE Access were fully aware of the criticisms and my responses to them throughout the two rounds of the review process.
***
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
97 posts
• Page 3 of 5 • 1, 2, 3, 4, 5
Return to Sci.Physics.Foundations
Who is online
Users browsing this forum: ahrefs [Bot] and 119 guests

