Heinera wrote:FrediFizzx wrote:I suspect you are misreading Gull's number (2). I think for "answer", he is talking about the correlation. And the correlation for each event will be 0 or 1. But I don't understand what he says, "Can be different between trials". ???
If anyone else has a clue about this, go ahead and chip in. Here is Gull's original proof.
http://www.mrao.cam.ac.uk/~steve/maxent ... s/bell.pdf.
The function p is simply the function that should give an output of 0 or 1, given the angle
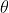
as input. There could be a different result for each n, which is why n is the second argument to the function (if you want, you can interpret n as the hidden variable

). At this stage in the proof, in other words (2), he is not talking about correlations.
Not 0 or 1, but -1 or +1, in Gull’s outline proof.
Gull is moreover implicitly assuming that the two computer programs do not use *memory* of *previous* inputs. Each program takes as inputs *only*: a trial number which I call “n” and an angle which I’ll call “theta” respectively. Let me call the two programs p and q. So we know that for all theta and all n, q(theta, n) = - p(theta, n). Because the programs are built so as to give equal and opposite outputs when given two identical streams of angles. Now suppose that the user supplied two arbitrary lists of angles, let me denote them by theta_1, theta_2, ... and phi_1, phi_2, .... Then the actual outputs of the n’th trial are p(theta_n, n) and -p(phi_n, n). Those are two numbers +/-1.
Now we are ready to start doing the interesting stuff.... suppose one stream is theta, theta, theta, ... and the other stream is phi, phi, phi ... The correlation is the limit as n goes to infinity of 1/n times the sum from 1 to n of minus p(n, theta) p(n, phi).
The next thing we are going to do is some Fourier transformation tricks. And also do something cunning with those two angles. I need to quickly take my own personal refresher course on Fourier series. The key thing is going to be that the Fourier transform of the *convolution* of two functions is the product of the transforms. My memory is hazy. I learnt that stuff 50 years ago, have occasionally touched on it while teaching “Banach and Hilbert spaces”, or “Functional Analysis”. But of course, QM is all about Fourier transformation. Riemann and then Lebesgue invented rigorous integration theories in order to fix practical problems with Fourier theory, which had huge military applications. And so the story went on (Banach, Hilbert, von Neumann ... particle physics, Einstein, E = m c^2, Werner Von Heisenberg, Nieks Bohr and quantum mechanics ... and then we had the nuclear bomb).

