Half-Integer Fractional Dirac Magnetic Monopole Charges
36 posts
• Page 1 of 2 • 1, 2
Half-Integer Fractional Dirac Magnetic Monopole Charges
To all:
I took a season away from physics for my son's wedding in August and to catch up with other things during what has been a very busy period of time for me. But I have recently returned to my work on Dirac monopoles, and just yesterday submitted the paper below for review at PRD:
http://vixra.org/pdf/1511.0151v1.pdf
This paper shows how half-integer Dirac charges come into being and are in fact required when an electron wavefunction traverses a magnetic monopole in a tidal lock, as opposed to traversing the monopole without rotation which leads to the usual integer Dirac charge quanta.
Over the next few months, I am planning to clearly develop the unification between electrodynamics and thermodynamics which can be reached by linking these half-integer charges to the half-integer charges which are in fact observed, but only at ultra-low temperatures near 0K, as part of the Fractional Quantum Hall Effect (FQHE). The fact that the observation of these half-integer charge quanta is directly tied to temperature makes clear qualitatively that there is some connection going on between electrodynamics and thermodynamics, which is to say, the electrodynamic quantization is clearly impacted by the thermodynamic environment. What I plan to do these next few months is to solidify the quantitative nature of this connection. The starting point will be this paper.
As a preview: we get to the odd-integer FQHE fractions by considering modified tidal locks using generalized roots of unity and not just square roots, with the odd-integer fractions being allowed and the other even-integer fractions except 2 prohibited by Lorentz symmetry as I have shown in some longer draft papers previously posted in this forum. It then further turns out that this underpins atomic structure, because the n/3, n/5, n/7, n/9 ... fractional FQHE states can be shown to also have respective total angular momenta j=3,5,7,9... and thus be the electrons in respective s, p, d, f... orbital shell states. The key to all of this is to show how the low-temperature symmetry between electric and magnetic charges is formally broken, and how the magnetic charges that exist near 0K melt into a thermal residue that is the closely related to the partition functions of thermodynamics and that has the precise same quantum characteristics as the electronic structure of the atoms.
Enjoy if you are interested, and comments are always welcome.
Best to all,
Jay
I took a season away from physics for my son's wedding in August and to catch up with other things during what has been a very busy period of time for me. But I have recently returned to my work on Dirac monopoles, and just yesterday submitted the paper below for review at PRD:
http://vixra.org/pdf/1511.0151v1.pdf
This paper shows how half-integer Dirac charges come into being and are in fact required when an electron wavefunction traverses a magnetic monopole in a tidal lock, as opposed to traversing the monopole without rotation which leads to the usual integer Dirac charge quanta.
Over the next few months, I am planning to clearly develop the unification between electrodynamics and thermodynamics which can be reached by linking these half-integer charges to the half-integer charges which are in fact observed, but only at ultra-low temperatures near 0K, as part of the Fractional Quantum Hall Effect (FQHE). The fact that the observation of these half-integer charge quanta is directly tied to temperature makes clear qualitatively that there is some connection going on between electrodynamics and thermodynamics, which is to say, the electrodynamic quantization is clearly impacted by the thermodynamic environment. What I plan to do these next few months is to solidify the quantitative nature of this connection. The starting point will be this paper.
As a preview: we get to the odd-integer FQHE fractions by considering modified tidal locks using generalized roots of unity and not just square roots, with the odd-integer fractions being allowed and the other even-integer fractions except 2 prohibited by Lorentz symmetry as I have shown in some longer draft papers previously posted in this forum. It then further turns out that this underpins atomic structure, because the n/3, n/5, n/7, n/9 ... fractional FQHE states can be shown to also have respective total angular momenta j=3,5,7,9... and thus be the electrons in respective s, p, d, f... orbital shell states. The key to all of this is to show how the low-temperature symmetry between electric and magnetic charges is formally broken, and how the magnetic charges that exist near 0K melt into a thermal residue that is the closely related to the partition functions of thermodynamics and that has the precise same quantum characteristics as the electronic structure of the atoms.
Enjoy if you are interested, and comments are always welcome.
Best to all,
Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Yesterday, the first draft of the paper was rejected by the PRD editors with the following statement:
In response, I added a new section 7 that can be viewed in v2 of the paper at:
http://vixra.org/pdf/1511.0151v2.pdf
And, I wrote back the following to the editors:
What I will also add here is that I believe this rejection is a red herring. First, it is not clear to me (and maybe I am missing something?) why it would be a problem even if the half integer charges could be detectable by a spin-zero charged particle (which I show in the new section 7 they cannot). Second, a spin zero charged scalar is a hypothetical entity which according to known empirical and theoretical data (and I exclude super-symmetry which remains speculative) does not exist in the natural world. Specifically, in electroweak theory, the symmetry must be broken via to ensure that the electric charge is conserved and the photon is massless. So it seems to me to be a red herring to hypothesize a charged scalar particle to reject a manuscript when settled theory and empirical data tells us there is no such thing as a charged scalar particle.
to ensure that the electric charge is conserved and the photon is massless. So it seems to me to be a red herring to hypothesize a charged scalar particle to reject a manuscript when settled theory and empirical data tells us there is no such thing as a charged scalar particle.
I will keep everyone apprised as this progresses.
Jay
PRD wrote:The half-integer magnetic monopoles that you propose would clearly be detectable by a spin-zero charged particle. Your manuscript is incorrect, and we therefore cannot accept it for publication.
In response, I added a new section 7 that can be viewed in v2 of the paper at:
http://vixra.org/pdf/1511.0151v2.pdf
And, I wrote back the following to the editors:
In my repy I wrote:In your manuscript rejection earlier today, you stated that the half-integer magnetic monopoles I propose would clearly be detectable by a spin-zero charged particle. I disagree. A spin zero charged particle, being a boson that does not invert its version under 2π rotations in the same way as fermions, would only detect the customary whole-integer magnetic monopoles. I have uploaded a revised manuscript containing a new section 7 which details this.
I thank you for your review, however, because I had not thought about what would happen if one used a hypothetical scalar electron rather than a spin-half electron to traverse the monopole. I am glad to have now realized that these half-integer Dirac charges are uniquely detectable only by fermions, not bosons.
What I will also add here is that I believe this rejection is a red herring. First, it is not clear to me (and maybe I am missing something?) why it would be a problem even if the half integer charges could be detectable by a spin-zero charged particle (which I show in the new section 7 they cannot). Second, a spin zero charged scalar is a hypothetical entity which according to known empirical and theoretical data (and I exclude super-symmetry which remains speculative) does not exist in the natural world. Specifically, in electroweak theory, the symmetry must be broken via
I will keep everyone apprised as this progresses.
Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Hi Jay,
I recently wrote the following (viewtopic.php?f=6&t=211)
"Le Tho Hue and Le Duc Ninh (October 2015) presented a mathematical model, “The Simplest 3-3-1 Model” on arxiv, predicting electron-like particles with -1/2 charge and also particles with -1/6 electron charge. That mathematical model may prove very appropriate for preons or at least a good starting point for them. Preon A is basically a left-handed electron but with charge only -0.5. Preon C is the other half of the left-handed electron. Preon B is a right-handed electron with charge reduced to -0.5. Preon C is again the other half. ..."
Reference: Le Tho Hue, Le Duc Ninh (October 2015) “The simplest 3-3-1 model”. arXiv:1510.00302 [hep-ph]
I emailed Ninh at Berlin University and was very pleased to receive a pleasant reply. He wrote that he had already begun to wonder about preons to fit his predictions. Just one of his minor thought pathways presumably.
Note that my preon C has electric charge -0.5 and spin zero. Hypothetical preon, of course.
I cannot make a first generation elementary particle (i.e with four preons) with 1/2 charge. Each of my four preons has charge -1/2 and the antipreons have charge +1/2. And you cannot make a total of a half charge out of four such preons. (So you can't make one at all! You can only get -2, -1, 0, +1 or +2.) The nearest I can make is AECC' which has charge -1 and zero spin.
However, my preon C is a particle of sorts. My preon A fits quite well (I think) with what Ninh is predicting: something like an electron but with -1/2 charge instead of unit charge. I think he is hoping his prediction maybe will be found one day in experiments.
My own idea, which I am slowly working at for my next model, is that the preons have net colour, and like the quarks, they will not be seen as free particles. Or they may have colour-anticolour like gluons and still not be seen as free particles. So I would not hold my breath waiting for experimentalists to find a free preon or a free half charge scalar elementary particle, or even composite particle. Even if they don't have net colour, they have colour in every bit of them so you could still have colour forces between preons, but maybe not the known forces.
[NB I was not completely clear if the reviewer's criticism depended on a hypothetical half charge scalar boson or a scalar boson of any non-zero electric charge.]
Best wishes
I recently wrote the following (viewtopic.php?f=6&t=211)
"Le Tho Hue and Le Duc Ninh (October 2015) presented a mathematical model, “The Simplest 3-3-1 Model” on arxiv, predicting electron-like particles with -1/2 charge and also particles with -1/6 electron charge. That mathematical model may prove very appropriate for preons or at least a good starting point for them. Preon A is basically a left-handed electron but with charge only -0.5. Preon C is the other half of the left-handed electron. Preon B is a right-handed electron with charge reduced to -0.5. Preon C is again the other half. ..."
Reference: Le Tho Hue, Le Duc Ninh (October 2015) “The simplest 3-3-1 model”. arXiv:1510.00302 [hep-ph]
I emailed Ninh at Berlin University and was very pleased to receive a pleasant reply. He wrote that he had already begun to wonder about preons to fit his predictions. Just one of his minor thought pathways presumably.
Note that my preon C has electric charge -0.5 and spin zero. Hypothetical preon, of course.
I cannot make a first generation elementary particle (i.e with four preons) with 1/2 charge. Each of my four preons has charge -1/2 and the antipreons have charge +1/2. And you cannot make a total of a half charge out of four such preons. (So you can't make one at all! You can only get -2, -1, 0, +1 or +2.) The nearest I can make is AECC' which has charge -1 and zero spin.
However, my preon C is a particle of sorts. My preon A fits quite well (I think) with what Ninh is predicting: something like an electron but with -1/2 charge instead of unit charge. I think he is hoping his prediction maybe will be found one day in experiments.
My own idea, which I am slowly working at for my next model, is that the preons have net colour, and like the quarks, they will not be seen as free particles. Or they may have colour-anticolour like gluons and still not be seen as free particles. So I would not hold my breath waiting for experimentalists to find a free preon or a free half charge scalar elementary particle, or even composite particle. Even if they don't have net colour, they have colour in every bit of them so you could still have colour forces between preons, but maybe not the known forces.
[NB I was not completely clear if the reviewer's criticism depended on a hypothetical half charge scalar boson or a scalar boson of any non-zero electric charge.]
Best wishes
- Ben6993
- Posts: 287
- Joined: Sun Feb 09, 2014 12:53 pm
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Ben6993 wrote:[NB I was not completely clear if the reviewer's criticism depended on a hypothetical half charge scalar boson or a scalar boson of any non-zero electric charge.]
Best wishes
Hi Ben,
I do not at this time see any connection of the integer-charged Dirac monopoles or my half integer charges to a preon model. If there was to be a connection, it would have to start with a preon model that includes electrons.
I think the reviewer had in mind any non-zero electric charge, because any such charge would interact in a magnetic field. I made reference to a scalar electron in my new section 7 just as a convenient apples-to-apples straw man to compare to a spin 1/2 electron. Such a scalar electron would be plausible to anybody who believes in supersymmetric theory; I am not a believer, unless and until I see some empirical support for spin-0 copies of the quarks and leptons.
Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Yablon wrote:In my repy I wrote:In your manuscript rejection earlier today, you stated that the half-integer magnetic monopoles I propose would clearly be detectable by a spin-zero charged particle. I disagree. A spin zero charged particle, being a boson that does not invert its version under 2π rotations in the same way as fermions, would only detect the customary whole-integer magnetic monopoles. I have uploaded a revised manuscript containing a new section 7 which details this.
I thank you for your review, however, because I had not thought about what would happen if one used a hypothetical scalar electron rather than a spin-half electron to traverse the monopole. I am glad to have now realized that these half-integer Dirac charges are uniquely detectable only by fermions, not bosons.
Well, today the revised paper was rejected again, with the following bald statement:
PRD wrote:I regret to say that your response and revisions are unpersuasive, and that I still conclude that your manuscript is not suitable for Physical Review D. If you still wish to pursue publication of this material, you must submit it elsewhere.
Am I wrong to view PRD (Weinberg) as being off base for giving absolutely no substantive reason for his refusal to consider the paper any further? If there is something specific that is wrong, he needs, IMHO to point that out. How does one battle against a journal's unwillingness to give a substantive reason for a rejection, and only give the totally dodgy "not suitable"? Am I being objective in believing that the only thing wring with my paper is that its author is an independent researcher who is not a member of "the club"?
In any event, I have resubmitted to a different journal.
Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
I also just sent the following back to PRD:
I am tired of non-specific "not suitable" rejections which owe more the the fact that I am unaffiliated with a name institution and so these editors are unwilling to put in the the time to really review my work. I have been on this merry-go-round too many times, and I am not rolling over any longer.
Jay
Yablon in repy to PRD wrote:I would find to helpful to know why this paper is “not suitable” for publication in PRD. Can you pinpoint a flaw in the mathematical development that leads to my equation (5.14) for the half-integer charges? If not, I would like to know why you will not consider publishing this paper even if you cannot pinpoint a flaw in the development that leads to the main result. Unlike in the papers submitted earlier this year, I have confined myself to 2pi circuits and have still found that these circuits admit half-integer charges when the electrons used to detect the monopole are in a tidal lock with the monopole, because of spinor version reversal. These version reversals are well-settled, accepted physics; they simply have never to my knowledge been accounted for in the study of Dirac monopoles. I have also accounted fully for all of the other suggestions and critiques that you have provided since I first started to consider fractionalized Dirac charges a year ago. If there is no logical flaw you can point to in the present manuscript DL11770, then this is an important, new result to report.
I am tired of non-specific "not suitable" rejections which owe more the the fact that I am unaffiliated with a name institution and so these editors are unwilling to put in the the time to really review my work. I have been on this merry-go-round too many times, and I am not rolling over any longer.
Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Yablon wrote:I also just sent the following back to PRD:Yablon in repy to PRD wrote:I would find to helpful to know why this paper is “not suitable” for publication in PRD. Can you pinpoint a flaw in the mathematical development that leads to my equation (5.14) for the half-integer charges? If not, I would like to know why you will not consider publishing this paper even if you cannot pinpoint a flaw in the development that leads to the main result. Unlike in the papers submitted earlier this year, I have confined myself to 2pi circuits and have still found that these circuits admit half-integer charges when the electrons used to detect the monopole are in a tidal lock with the monopole, because of spinor version reversal. These version reversals are well-settled, accepted physics; they simply have never to my knowledge been accounted for in the study of Dirac monopoles. I have also accounted fully for all of the other suggestions and critiques that you have provided since I first started to consider fractionalized Dirac charges a year ago. If there is no logical flaw you can point to in the present manuscript DL11770, then this is an important, new result to report.
I am tired of non-specific "not suitable" rejections which owe more the the fact that I am unaffiliated with a name institution and so these editors are unwilling to put in the the time to really review my work. I have been on this merry-go-round too many times, and I am not rolling over any longer.
Jay
Hi Jay,
I fully sympathize with your frustration. Sadly, publication process in physics has become more of a political game than just reporting valid results.
Best,
Joy
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Joy Christian wrote:Hi Jay,
I fully sympathize with your frustration. Sadly, publication process in physics has become more of a political game than just reporting valid results.
Best,
Joy
Thanks Joy! I will be in touch privately to bounce some ideas. Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Yablon in repy to PRD wrote:I would find to helpful to know why this paper is “not suitable” for publication in PRD. Can you pinpoint a flaw in the mathematical development that leads to my equation (5.14) for the half-integer charges? If not, I would like to know why you will not consider publishing this paper even if you cannot pinpoint a flaw in the development that leads to the main result. Unlike in the papers submitted earlier this year, I have confined myself to 2pi circuits and have still found that these circuits admit half-integer charges when the electrons used to detect the monopole are in a tidal lock with the monopole, because of spinor version reversal. These version reversals are well-settled, accepted physics; they simply have never to my knowledge been accounted for in the study of Dirac monopoles. I have also accounted fully for all of the other suggestions and critiques that you have provided since I first started to consider fractionalized Dirac charges a year ago. If there is no logical flaw you can point to in the present manuscript DL11770, then this is an important, new result to report.
Twice, I submitted the response above. Twice, within minutes, they returned my paper to a "not under active consideration" status. So I am now appealing. This is what I just sent in:
Yablon in an appeal to PRD wrote:I have twice today responded to ask why this paper is “not suitable” for publication in PRD, and whether you can pinpoint a flaw in the mathematical development that leads to my equation (5.14) for the half-integer charges. Twice, in response, my paper was summarily returned within a matter of minutes to the status of "not under active consideration."
In accordance with the APS appeal procedures, and absent a response to my reasonable queries to obtain a substantive reason for this rejection, I HEREBY APPEAL THE REJECTION of this paper by the editors.
Yours sincerely,
Jay R. Yablon
I am curious as to whether they really do follow an appeal process, or just say so on paper because it looks nice.
Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
And in reply to my attempt to appeal, they still shunted this back to inactive status in the few minutes it took me to write this email. So I just sent the following back in:
Yablon wrote:I HEREBY APPEAL THE REJECTION FOR REASONS STATED. PLEASE DO NOT DISMISS THIS BACK TO INACTIVE STATUS.
Yablon wrote:Yablon in repy to PRD wrote:I would find to helpful to know why this paper is “not suitable” for publication in PRD. Can you pinpoint a flaw in the mathematical development that leads to my equation (5.14) for the half-integer charges? If not, I would like to know why you will not consider publishing this paper even if you cannot pinpoint a flaw in the development that leads to the main result. Unlike in the papers submitted earlier this year, I have confined myself to 2pi circuits and have still found that these circuits admit half-integer charges when the electrons used to detect the monopole are in a tidal lock with the monopole, because of spinor version reversal. These version reversals are well-settled, accepted physics; they simply have never to my knowledge been accounted for in the study of Dirac monopoles. I have also accounted fully for all of the other suggestions and critiques that you have provided since I first started to consider fractionalized Dirac charges a year ago. If there is no logical flaw you can point to in the present manuscript DL11770, then this is an important, new result to report.
Twice, I submitted the response above. Twice, within minutes, they returned my paper to a "not under active consideration" status. So I am now appealing. This is what I just sent in:Yablon in an appeal to PRD wrote:I have twice today responded to ask why this paper is “not suitable” for publication in PRD, and whether you can pinpoint a flaw in the mathematical development that leads to my equation (5.14) for the half-integer charges. Twice, in response, my paper was summarily returned within a matter of minutes to the status of "not under active consideration."
In accordance with the APS appeal procedures, and absent a response to my reasonable queries to obtain a substantive reason for this rejection, I HEREBY APPEAL THE REJECTION of this paper by the editors.
Yours sincerely,
Jay R. Yablon
I am curious as to whether they really do follow an appeal process, or just say so on paper because it looks nice.
Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Yablon wrote:I am curious as to whether they really do follow an appeal process, or just say so on paper because it looks nice.
Since you have followed somewhat informal dialogue with the Chief Editor of PRD, it is not clear to me what their reaction would be. But according to their rules if you formally appeal, like you have, then they are obliged to send your entire file to a member of the editorial board, or an external adjudicator appointed by them. He or she will then have to write a signed report on your paper, with recommendations to the editors. So if your paper does go through a formal appeal, then you will get a signed report from some academically established physicist.
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Joy Christian wrote:Yablon wrote:I am curious as to whether they really do follow an appeal process, or just say so on paper because it looks nice.
Since you have followed somewhat informal dialogue with the Chief Editor of PRD, it is not clear to me what their reaction would be. But according to their rules if you formally appeal, like you have, then they are obliged to send your entire file to a member of the editorial board, or an external adjudicator appointed by them. He or she will then have to write a signed report on your paper, with recommendations to the editors. So if your paper does go through a formal appeal, then you will get a signed report from some academically established physicist.
I have not had the informal dialogue in about a year. I followed the formal submission process for this paper to the letter and had no "out of court" communications with Erick Weinberg at all. I think that at this point he is too close to this work to be objective. He has provided good substantive critique over the past year, and I had hoped that once I dealt with those critiques and fixed anything that needed to be fixed, then they would accept the paper. But instead, now that I seem to have arrived at that point of nothing left that is wrong, he is simply saying "no" without giving any reason.
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Mr. Yablon,
Both the initial and final rejections (or at least what you
have quoted of them) seem spurious. I think that your reply persuasively
questioned the initial rejection. Were I to receive a similarly
superficial rejection, I would surely be annoyed.
That said, I can't follow your paper in detail but to the
extent that I understand it, it does seem questionable at some
crucial points. I have neither space nor time to explain here,
but I will mention just a few.
BEGIN TECHNICAL ANALYSIS
This group is new to me, I'm not sure how to post using
mathematical symbols, and I don't have time right now to learn.
So, I will attempt to write in ASCII, spelling out symbols such
as Greek letters.
Your equation (2.1) starts by defining a transformation law
psi --> exp(i Lambda) psi
where the real function Lambda is cryptically described as a
phase angle which "varies locally". I take "varies locally"
to mean that Lambda is not well defined globally
but can be multiple-valued. This vagueness at the very start makes
the paper difficult to read because one is never sure precisely how
to interpret the symbols.
Dirac uses a similar transformation, but he describes more
clearly his meaning. He is essentially proposing a new interpretation
of quantum mechanics in which *all* wave functions are multiplied by
the same Lambda. He justifies this assumption by noticing that this
would not change transition probabilities. But it does change other
things even if Lambda is globally single valued, such as the expectation
of most observables. It is a radical modification of standard quantum
mechanics, which is open to question. At a minimum, it deserves more
discussion than either he or you gives.
Dirac's argument involves the change in Lambda (phase change
of psi) as one traverses certain closed loops.
This change does not necessarily vanish as it would for a single-valued
Lambda.
Dirac's change in Lambda is due to the potentials for a magnetic
monopole being not globally defined (equivalently, defined but
multiple valued). You appear to add to this change a change attributed
to the fact that when described by quantum mechanics, changing coordinates
by a physical rotation (member of the rotation group SO(3)) is described
by a member of the simply connected covering group SU(2) for SO(3).
To each member of SO(3) correspond precisely two members of SU(2).
It is these members of SU(2), not the original member of SO(3),
which act on wave functions.
If we have a quantum system described by certain coordinates, and we rotate
the coordinates through an angle phi and ask how the system looks in the
new coordinates, there are two possible answers corresponding to the two
elements of SU(2) which map to the single rotation by phi in SO(3).
But these two answers are not really different --- they differ only in
multiplying *all* wave functions by (-1), which doesn't actually change the
wave function, which is only determined up to a phase anyway.
Suppose now that the rotation angle is 360 degrees, but the rotation
is conceived as a series of much smaller rotations. A smaller rotation,
say through 5 degrees, is more naturally described that way than as a
rotation through 365 = 360 + 5 degrees, which gives a unique choice of
the element of SU(2) describing the rotation.
Putting together that description of the smaller rotations,
one might conclude that a 360 degree rotation
changes psi by a factor of (-1). But this is just an illusion, a
book-keeping device. There is no actual change in psi because psi
was only determined up to a phase to begin with.
In addition, if you read Dirac carefully, you will see that he never
considers moving his electron around the small loops that he considers.
He only integrates the monopole field over surfaces bounded by the loops.
So far as I can see, your apparent addition of a phase of 180 degrees
(factor of -1 for the wave function) to the change in potential around the
loop is physically unjustified. Perhaps I misinterpret what you have done,
but at a minimum it seems that more extensive and clearer explanation is
required before people can regard your argument as persuasive.
END OF TECHNICAL ANALYSIS
Irregardless of the correctness of your paper,
You have been badly treated by Phys. Rev. D (PRD). Very probably,
your paper was never read with any care. Very probably, your response
to the initial rejection was never seriously considered.
Very probably, your suspicion is correct that the real reason
for the rejection was that "its author is an independent researcher
who is not a member of 'the club'".
All the Phys. Rev. journals with which I have experience
(Phys. Rev. A, Phys. Rev. D, Phys. Rev. Letters) are that way.
Nearly all physics journals are that way.
What can be done, other than giving up? I would bet that
your chances of being published in a mainstream journal are small
irrespective of the quality of the submissions. That is just
the way things are, the way that in some countries one adjusts to
pervasive corruption as a fact of life.
`But a small chance is not the same as no chance. Submissions
which are unclear or arguably incorrect can convert a small chance to
no chance. Refereeing is a time-consuming and generally thankless task.
One cannot expect a referee to read a paper carefully multiple times
corresponding to various plausible guesses at the meaning of symbols.
To have a chance, crystal clarity of the exposition and correctness
of the arguments is essential. I would recommend finding some
knowledgeable friend or acquaintance to carefully read your papers before
submission. If you can't find such a person, then it would be reasonable
to ask who will ever read a published version.
There seem to be hundreds of users of this forum. Can it be that
none are qualified to read your paper? It doesn't require any special
knowledge, only a professional understanding of quantum mechanics.
Also keep in mind that no one is likely to offer to donate his
time if he doesn't think that there is a reasonable chance that the paper
is correct. In my case, my doubts are sufficiently strong that I probably
wouldn't.
Nevertheless, I am disgusted by how you have been treated.
That is why I have taken time to write this.
From your writings I can tell that you are a serious person who deserves
much better.
Both the initial and final rejections (or at least what you
have quoted of them) seem spurious. I think that your reply persuasively
questioned the initial rejection. Were I to receive a similarly
superficial rejection, I would surely be annoyed.
That said, I can't follow your paper in detail but to the
extent that I understand it, it does seem questionable at some
crucial points. I have neither space nor time to explain here,
but I will mention just a few.
BEGIN TECHNICAL ANALYSIS
This group is new to me, I'm not sure how to post using
mathematical symbols, and I don't have time right now to learn.
So, I will attempt to write in ASCII, spelling out symbols such
as Greek letters.
Your equation (2.1) starts by defining a transformation law
psi --> exp(i Lambda) psi
where the real function Lambda is cryptically described as a
phase angle which "varies locally". I take "varies locally"
to mean that Lambda is not well defined globally
but can be multiple-valued. This vagueness at the very start makes
the paper difficult to read because one is never sure precisely how
to interpret the symbols.
Dirac uses a similar transformation, but he describes more
clearly his meaning. He is essentially proposing a new interpretation
of quantum mechanics in which *all* wave functions are multiplied by
the same Lambda. He justifies this assumption by noticing that this
would not change transition probabilities. But it does change other
things even if Lambda is globally single valued, such as the expectation
of most observables. It is a radical modification of standard quantum
mechanics, which is open to question. At a minimum, it deserves more
discussion than either he or you gives.
Dirac's argument involves the change in Lambda (phase change
of psi) as one traverses certain closed loops.
This change does not necessarily vanish as it would for a single-valued
Lambda.
Dirac's change in Lambda is due to the potentials for a magnetic
monopole being not globally defined (equivalently, defined but
multiple valued). You appear to add to this change a change attributed
to the fact that when described by quantum mechanics, changing coordinates
by a physical rotation (member of the rotation group SO(3)) is described
by a member of the simply connected covering group SU(2) for SO(3).
To each member of SO(3) correspond precisely two members of SU(2).
It is these members of SU(2), not the original member of SO(3),
which act on wave functions.
If we have a quantum system described by certain coordinates, and we rotate
the coordinates through an angle phi and ask how the system looks in the
new coordinates, there are two possible answers corresponding to the two
elements of SU(2) which map to the single rotation by phi in SO(3).
But these two answers are not really different --- they differ only in
multiplying *all* wave functions by (-1), which doesn't actually change the
wave function, which is only determined up to a phase anyway.
Suppose now that the rotation angle is 360 degrees, but the rotation
is conceived as a series of much smaller rotations. A smaller rotation,
say through 5 degrees, is more naturally described that way than as a
rotation through 365 = 360 + 5 degrees, which gives a unique choice of
the element of SU(2) describing the rotation.
Putting together that description of the smaller rotations,
one might conclude that a 360 degree rotation
changes psi by a factor of (-1). But this is just an illusion, a
book-keeping device. There is no actual change in psi because psi
was only determined up to a phase to begin with.
In addition, if you read Dirac carefully, you will see that he never
considers moving his electron around the small loops that he considers.
He only integrates the monopole field over surfaces bounded by the loops.
So far as I can see, your apparent addition of a phase of 180 degrees
(factor of -1 for the wave function) to the change in potential around the
loop is physically unjustified. Perhaps I misinterpret what you have done,
but at a minimum it seems that more extensive and clearer explanation is
required before people can regard your argument as persuasive.
END OF TECHNICAL ANALYSIS
Irregardless of the correctness of your paper,
You have been badly treated by Phys. Rev. D (PRD). Very probably,
your paper was never read with any care. Very probably, your response
to the initial rejection was never seriously considered.
Very probably, your suspicion is correct that the real reason
for the rejection was that "its author is an independent researcher
who is not a member of 'the club'".
All the Phys. Rev. journals with which I have experience
(Phys. Rev. A, Phys. Rev. D, Phys. Rev. Letters) are that way.
Nearly all physics journals are that way.
What can be done, other than giving up? I would bet that
your chances of being published in a mainstream journal are small
irrespective of the quality of the submissions. That is just
the way things are, the way that in some countries one adjusts to
pervasive corruption as a fact of life.
`But a small chance is not the same as no chance. Submissions
which are unclear or arguably incorrect can convert a small chance to
no chance. Refereeing is a time-consuming and generally thankless task.
One cannot expect a referee to read a paper carefully multiple times
corresponding to various plausible guesses at the meaning of symbols.
To have a chance, crystal clarity of the exposition and correctness
of the arguments is essential. I would recommend finding some
knowledgeable friend or acquaintance to carefully read your papers before
submission. If you can't find such a person, then it would be reasonable
to ask who will ever read a published version.
There seem to be hundreds of users of this forum. Can it be that
none are qualified to read your paper? It doesn't require any special
knowledge, only a professional understanding of quantum mechanics.
Also keep in mind that no one is likely to offer to donate his
time if he doesn't think that there is a reasonable chance that the paper
is correct. In my case, my doubts are sufficiently strong that I probably
wouldn't.
Nevertheless, I am disgusted by how you have been treated.
That is why I have taken time to write this.
From your writings I can tell that you are a serious person who deserves
much better.
- guest1202
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
guest1202 wrote:So far as I can see, your apparent addition of a phase of 180 degrees (factor of -1 for the wave function) to the change in potential around the loop is physically unjustified. Perhaps I misinterpret what you have done, but at a minimum it seems that more extensive and clearer explanation is required before people can regard your argument as persuasive.
Hello guest1202, and welcome to the discussions here.
I will state without hesitation that the half-integer charges result from the factor of -1 that changes the wavefunction after a
To facilitate the discussion, may I refer to you reference [11] of my paper, which is at http://sites.math.northwestern.edu/~cel ... n_talk.pdf. Section 3 near the bottom of page 3 also builds up the travel around the closed loop by small increments and suggests that the wavefunction must be single-valued once the whole loop is completed. Can you please take a look at that reference, then let me know how you think this bears on your technical analysis, and what would happen according to that analysis if the electron was in a tidal lock with the monopole and so also underwent a
Thanks,
Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
guest1202 wrote:Your equation (2.1) starts by defining a transformation law
where the real function Lambda is cryptically described as a phase angle which "varies locally". I take "varies locally" to mean that Lambda is not well defined globally but can be multiple-valued. This vagueness at the very start makes the paper difficult to read because one is never sure precisely how to interpret the symbols.
Dear guest1202 (and maybe you should get yourself a user name so that your posts will go straight up without awaiting moderation):
I am actually surprised to read the comment that this is vague. This is just a local U(1)_em gauge transformation -- found in any of dozen of places -- though we know that "gauge" parameter is really a historical misnomer for a "phase" because it took Hermann Weyl about a dozen years to realize that the exponential he used to transform a wavefunction had to have an imaginary
The requirement of single-valuedness -- which comes into play when we talk about electrons near monopoles but probably applies in other circumstances as well -- is that as between a first point and a second point which is the same as the first point, the wavefunction as it lives in SU(2) must be exactly the same without any rotation in the Euler plane. So if the wavefunction is in a tidal lock and its sign gets inverted because it has gone through a
Let me make one other comment beyond the scope of this paper, to provide a sense of where I will go with all of this, physically: I envision (and will write up) that near 0K there is a low-temperature electric / magnetic duality. Dirac monopoles come into being near 0K but quickly "melt" at higher temperatures. When these monopoles do exist, there will be interaction forces between monopole charges that are
Anyway, getting back, what might I have said that I did not say to have the symbols in (2.1) not be vague, when all I am meaning to say is that this is a U(1)_em gauge transformation? Maybe that is all I should say and I said too much? I would sure hate to see somebody get hung up at (2.1) for lack of clarity.
Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Mr. Yablon,
Your question about how you could clarify the meaning of
your basic transformation law
psi --> exp(i Lambda) psi
deserves a better answer than space and time permit me to give.
I'll just make a few remarks which I think could be fleshed out into
a satisfactory answer. However, to do so would require almost a
chapter of a book.
BEGIN ANSWER TO "CLARIFICATION" QUESTION
Dirac's analysis was framed is a setting of standard quantum
mechanics in which a "state" is a nonzero complex-valued
square-integrable function on three-dimensional real Euclidean space R^3,
with the important caveat:
TWO SUCH FUNCTIONS ARE CONSIDERED THE "SAME" IF EACH OF THEM
IS A NONZERO COMPLEX SCALAR MULTIPLE OF THE OTHER .
Two functions psi and phi are considered as representing the "same" state if
phi = c phi
for some nonzero complex constant c. Colloquially, phi is called
a "wavefunction", and the caveat is ignored in talking about it.
However, sometimes one can't ignore the caveat, and your context is
one of these times, as I shall try to explain below.
In short, a "wavefunction" is not really a function, but is an
equivalence class of functions related as just described.
Suppose we have such an equivalence class and we choose
one particular wavefunction phi to represent the class. Consider
a "base point" *b* in R^3 and a loop starting and ending at *b*.
Consider values phi(x) for *x* starting at *b*, going around the loop,
and ending at *b*. Of course, the ending value has to be the same
as the beginning value, assuming that phi is single-valued. If we
allow phi to be multiple-valued, this is no longer true. However,
what is true if we take the caveat into account is that the ending value
must equal the beginning value times some constant *c*, where
*c* IS THE SAME FOR ALL BASE POINTS.
In your case for a loop described by a 360 degree rotation,
c = -1, and is the same for *all* base points and for *all* wavefunctions
(including those not in phi's equivalence class). This is because
the endpoint of the rotation loop is of the form (U phi)(b) with U
the unitary operator which is (-1) times the identity operator.
(The beginning point is of the same form with *U* the identity.)
This does not mean that phi is multiple-valued, which is not allowed
in standard quantum mechanics.
What I just said is the most important thing to understand,
but it doesn't directly address your question about how to clarify
what you mean by (2.1), your basic transformation law
psi --> exp(i Lambda) psi .
First of all, are you assuming a setting of standard quantum mechanics
as above, or are you assuming quantum states are sections
of a what one might call a "projective line bundle"?
[I mean a complex line bundle with two sections considered
the "same" if they differ by a nonzero complex constant *c*.
I'm not sure if there is a standard name for such an object.]
If you are assuming standard quantum mechanics, the function Lambda would
have to be single-valued, but I suspect that you are assuming that
Lambda could be multiple-valued as suggested by your cryptic language
that Lambda "varies locally". That is not standard mathematical language,
and I haven't seen it in physics jargon either.
Finally, I'll touch on your question as to how this discussion
relates to your reference (11) (an expository talk at Northwestern
University). The speaker seems to ignore the distinction between
a complex line bundle and what I called a "projective line bundle"
above. For his mathematical purposes, he can (and seems to) use
only regular (not projective) line bundles. In that context,
it is correct that following the values of a section around a loop
must end with the same value as the value at the beginning of the loop,
but that is no longer true for a projective line bundle. For your
considerations, the distinction is important; for his, it isn't.
END OF PARTIAL ANSWER TO "CLARIFICATION" QUESTION
I suspect that the above answer may be hard to follow because
it relies a common understanding of the framework of quantum mechanics,
and yours may differ from mine. Next I'll ask about a more elementary
assertion of your paper point which puzzles me,
and which I suspect may contain a fundamental error.
Before starting, it might be helpful to remark that your paper
seems to attach significance to "fractional charges". What, precisely,
do you consider a "fractional charge"? I would take this to mean
a fraction of the charge of an electron. The following assumes that
this is in fact the meaning.
BEGIN DISCUSSION OF YOUR EQUATIONS (4.7) AND (4.8).
The paper's equation (4.7) states the "Dirac Quantization Condition":
(4.7) 2eg = n .
Here *e* is the electronic charge, *g* the monopole's "magnetic charge",
and *n* an arbitrary nonzero integer. The paper goes on:
"From (4.7), defining the n=1 charge units as e_0 = 1/2g
and g_0 = 1/2e, we see that the respective electric
and magnetic charge strengths are reciprocally quantized by
(4.8) e = n/2g = n e_0
g = n/23 = n g_0 . "
This seems to be circular logic: e is defined in terms of g while
g is defined in terms of e. Morever, I think that the preceding sentence
should read: e_0 = 1/2g_0 and g_0 = 1/2 e_0 .
The effect is that neither e_0 nor g_0 are actually defined.
Later in its equation (5.15) the paper states that for n = 1,
e = 1/2 e_0. Assuming that the "e" and "e_0" in (5.15) are the same
as in (4.8), this seems to be a contradiction.
I've wondered if this could be attributable to a mere typo,
but I haven't been able to think of definitions for the symbols for
which all these claims make sense. Were I a referee, I would stop
reading at this point and either reject the paper or send it back for
clarification if I thought that there might be some hope that the paper
was essentially correct.
To get back to the question of the meaning of "fractional charges",
every real number is 1/2 of some other real number!
The question is what it means to write
e = (1/2) e_0 .
My best guess is that e_0 might represent the charge of an electron,
but I can't find that explicitly stated in the paper. A reader should
not have to make such guesses. As noted above, the definition of e_0
around (4.8) does not seem to make sense.
END DISCUSSION OF (4.7) and (4.8)
Regarding your suggestion that I register as a member of this
group, I prefer to remain anonymous because of the frequently toxic
and insulting language of some of the regular posters, particularly
regarding the discussion of Bell's inequalities. I don't want to be
associated in any way with a group which tolerates such incivility.
I happen to be intimately familiar with issues surrounding
Bell's theorem (much more so than with Dirac quantization), and think that
most of the regular posters are misguided. If they would only listen
respectfully to each other, they should come to agreement in no time.
Basically, they are arguing over definitions.
Also, my time is very limited, and I can't afford to become
embroiled in endless discussions of ill-defined issues. Already,
I am beginning to regret my initial post. I only submitted it because
it seemed offensive that the response of Phys. Rev. D (PRD) to your paper was
so blatantly deficient.
Speaking of PRD, that reminds me that you are likely to get into
trouble if you are appealing the PRD rejection at the same time as
submitting the paper elsewhere. Most journals (including PRD if I recall
correctly) require an author to represent that his submitted paper
is not under consideration elsewhere. If it is under appeal with PRD,
then technically it is still under consideration by PRD.
Also, I might remark that another poster wonders if the appeals
process of PRD is genuine or merely rubber-stamps a rejection. I have
experience with appeals to Phys. Rev. journals (though not with PRD),
and have found the appeals to be genuine. I had one rejected by
a rather reluctant Divisional Associate Editor (DAE), and another upheld
(i.e., the appeal was declared valid).
The integrity of the process depends entirely on the integrity of the
particular DAE to whom it is sent. I was lucky enough to get two with
integrity. (The rejection was not because of any claimed flaw in the paper,
but because the DAE thought that it was too technical to be comprehensible
to typical readers.)
However, I urge you to obtain an informal opinion from a source
which you trust before appealing or resubmitting.
Your question about how you could clarify the meaning of
your basic transformation law
psi --> exp(i Lambda) psi
deserves a better answer than space and time permit me to give.
I'll just make a few remarks which I think could be fleshed out into
a satisfactory answer. However, to do so would require almost a
chapter of a book.
BEGIN ANSWER TO "CLARIFICATION" QUESTION
Dirac's analysis was framed is a setting of standard quantum
mechanics in which a "state" is a nonzero complex-valued
square-integrable function on three-dimensional real Euclidean space R^3,
with the important caveat:
TWO SUCH FUNCTIONS ARE CONSIDERED THE "SAME" IF EACH OF THEM
IS A NONZERO COMPLEX SCALAR MULTIPLE OF THE OTHER .
Two functions psi and phi are considered as representing the "same" state if
phi = c phi
for some nonzero complex constant c. Colloquially, phi is called
a "wavefunction", and the caveat is ignored in talking about it.
However, sometimes one can't ignore the caveat, and your context is
one of these times, as I shall try to explain below.
In short, a "wavefunction" is not really a function, but is an
equivalence class of functions related as just described.
Suppose we have such an equivalence class and we choose
one particular wavefunction phi to represent the class. Consider
a "base point" *b* in R^3 and a loop starting and ending at *b*.
Consider values phi(x) for *x* starting at *b*, going around the loop,
and ending at *b*. Of course, the ending value has to be the same
as the beginning value, assuming that phi is single-valued. If we
allow phi to be multiple-valued, this is no longer true. However,
what is true if we take the caveat into account is that the ending value
must equal the beginning value times some constant *c*, where
*c* IS THE SAME FOR ALL BASE POINTS.
In your case for a loop described by a 360 degree rotation,
c = -1, and is the same for *all* base points and for *all* wavefunctions
(including those not in phi's equivalence class). This is because
the endpoint of the rotation loop is of the form (U phi)(b) with U
the unitary operator which is (-1) times the identity operator.
(The beginning point is of the same form with *U* the identity.)
This does not mean that phi is multiple-valued, which is not allowed
in standard quantum mechanics.
What I just said is the most important thing to understand,
but it doesn't directly address your question about how to clarify
what you mean by (2.1), your basic transformation law
psi --> exp(i Lambda) psi .
First of all, are you assuming a setting of standard quantum mechanics
as above, or are you assuming quantum states are sections
of a what one might call a "projective line bundle"?
[I mean a complex line bundle with two sections considered
the "same" if they differ by a nonzero complex constant *c*.
I'm not sure if there is a standard name for such an object.]
If you are assuming standard quantum mechanics, the function Lambda would
have to be single-valued, but I suspect that you are assuming that
Lambda could be multiple-valued as suggested by your cryptic language
that Lambda "varies locally". That is not standard mathematical language,
and I haven't seen it in physics jargon either.
Finally, I'll touch on your question as to how this discussion
relates to your reference (11) (an expository talk at Northwestern
University). The speaker seems to ignore the distinction between
a complex line bundle and what I called a "projective line bundle"
above. For his mathematical purposes, he can (and seems to) use
only regular (not projective) line bundles. In that context,
it is correct that following the values of a section around a loop
must end with the same value as the value at the beginning of the loop,
but that is no longer true for a projective line bundle. For your
considerations, the distinction is important; for his, it isn't.
END OF PARTIAL ANSWER TO "CLARIFICATION" QUESTION
I suspect that the above answer may be hard to follow because
it relies a common understanding of the framework of quantum mechanics,
and yours may differ from mine. Next I'll ask about a more elementary
assertion of your paper point which puzzles me,
and which I suspect may contain a fundamental error.
Before starting, it might be helpful to remark that your paper
seems to attach significance to "fractional charges". What, precisely,
do you consider a "fractional charge"? I would take this to mean
a fraction of the charge of an electron. The following assumes that
this is in fact the meaning.
BEGIN DISCUSSION OF YOUR EQUATIONS (4.7) AND (4.8).
The paper's equation (4.7) states the "Dirac Quantization Condition":
(4.7) 2eg = n .
Here *e* is the electronic charge, *g* the monopole's "magnetic charge",
and *n* an arbitrary nonzero integer. The paper goes on:
"From (4.7), defining the n=1 charge units as e_0 = 1/2g
and g_0 = 1/2e, we see that the respective electric
and magnetic charge strengths are reciprocally quantized by
(4.8) e = n/2g = n e_0
g = n/23 = n g_0 . "
This seems to be circular logic: e is defined in terms of g while
g is defined in terms of e. Morever, I think that the preceding sentence
should read: e_0 = 1/2g_0 and g_0 = 1/2 e_0 .
The effect is that neither e_0 nor g_0 are actually defined.
Later in its equation (5.15) the paper states that for n = 1,
e = 1/2 e_0. Assuming that the "e" and "e_0" in (5.15) are the same
as in (4.8), this seems to be a contradiction.
I've wondered if this could be attributable to a mere typo,
but I haven't been able to think of definitions for the symbols for
which all these claims make sense. Were I a referee, I would stop
reading at this point and either reject the paper or send it back for
clarification if I thought that there might be some hope that the paper
was essentially correct.
To get back to the question of the meaning of "fractional charges",
every real number is 1/2 of some other real number!
The question is what it means to write
e = (1/2) e_0 .
My best guess is that e_0 might represent the charge of an electron,
but I can't find that explicitly stated in the paper. A reader should
not have to make such guesses. As noted above, the definition of e_0
around (4.8) does not seem to make sense.
END DISCUSSION OF (4.7) and (4.8)
Regarding your suggestion that I register as a member of this
group, I prefer to remain anonymous because of the frequently toxic
and insulting language of some of the regular posters, particularly
regarding the discussion of Bell's inequalities. I don't want to be
associated in any way with a group which tolerates such incivility.
I happen to be intimately familiar with issues surrounding
Bell's theorem (much more so than with Dirac quantization), and think that
most of the regular posters are misguided. If they would only listen
respectfully to each other, they should come to agreement in no time.
Basically, they are arguing over definitions.
Also, my time is very limited, and I can't afford to become
embroiled in endless discussions of ill-defined issues. Already,
I am beginning to regret my initial post. I only submitted it because
it seemed offensive that the response of Phys. Rev. D (PRD) to your paper was
so blatantly deficient.
Speaking of PRD, that reminds me that you are likely to get into
trouble if you are appealing the PRD rejection at the same time as
submitting the paper elsewhere. Most journals (including PRD if I recall
correctly) require an author to represent that his submitted paper
is not under consideration elsewhere. If it is under appeal with PRD,
then technically it is still under consideration by PRD.
Also, I might remark that another poster wonders if the appeals
process of PRD is genuine or merely rubber-stamps a rejection. I have
experience with appeals to Phys. Rev. journals (though not with PRD),
and have found the appeals to be genuine. I had one rejected by
a rather reluctant Divisional Associate Editor (DAE), and another upheld
(i.e., the appeal was declared valid).
The integrity of the process depends entirely on the integrity of the
particular DAE to whom it is sent. I was lucky enough to get two with
integrity. (The rejection was not because of any claimed flaw in the paper,
but because the DAE thought that it was too technical to be comprehensible
to typical readers.)
However, I urge you to obtain an informal opinion from a source
which you trust before appealing or resubmitting.
- guest1202
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Well, I guess that I squeaked loudly enough to receive a substantive explanation on Thursday from PRD Editor Erick Weinberg of the paper rejection. What he said is the following:
In reply I wrote back:
Now let's talk about the physics of all of this. I will refer to the latest draft of my paper posted at http://vixra.org/pdf/1511.0151v2.pdf. I also want to thank guest1202 for another insightful recent post, I will get to that separately when I have a chance.
First, with this rejection, I understand the longer-term method to Weinberg's madness. He is the one who when rejecting a draft early in 2015 suggested that I explicitly derive the potentials for the Dirac magnetic monopoles as well as whatever fractional monopoles I was pursuing. I did so for the usual Dirac monopoles at (4.12), namely:
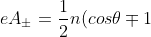d\phi) . (4.12)
. (4.12)
This potential is well known, see for example, the final set-off equation at https://www.encyclopediaofmath.org/inde ... c_monopole, which is a very good reference that I urge you to read if you are trying to follow this thread. Note that I use a reversed sign convention from this reference. No tidal lock in (4.12).
Following suit, at (5.16) I set out the monopole potential for a wavefunction which is in a tidal lock, namely:
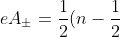(cos\theta\mp 1)d\phi) (5.16)
(5.16)
This is associated with my claimed half-integer Dirac monopole charges. It is easily seen that the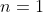 potential (5.16) is half a strong as the
potential (5.16) is half a strong as the  potential (4.12).
potential (4.12).
So here is what Weinberg is really saying, and in classical physics it is a perfectly correct argument: Equations (4.12) and (5.16) are both the equations for the electromagnetic vector potential one-form of a magnetic monopole. What you, Yablon, are telling me, is that if you detect the monopole with an electron that is not tidally locked, you get the potential (4.12). But then, if you detect the same monopole with an electron that is tidally locked, you get the different potential (5.16). But these potentials belong to the monopole itself. They should not depend on what you put into the potential to detect things. Further, the potential will of course determine the motions of electrons and other charged particles placed in that potential, because at the end of the day the magnetic monopole -- as unusual an object as it might be were it to exist -- is still creating a magnetic field indistinguishable from any ordinary magnetic field other than the fact that it has a monopolar field configuration, and we know from Maxwell and Lorentz how a charged particle will behave in a magnetic field. E&M 101. So how can you tell me that I can take an electron wavefunction, and have it respond as if the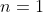 magnetic monopole potential is full strength when there is no tidal lock, but is half strength when there is a tidal lock? In order for that to happen, the potential of the monopole would have to be dependent on the wavefunction itself, rather than independent of the detecting wavefunction. And we know very well -- at least in classical electrodynamics -- that subject of course to choosing a "ground" which we handle formally through gauge symmetry, the potential is the potential, and whatever particles you run through that potential do not charge the potential, except insofar as those objects generate their own potentials. Further, nobody would ever contend that if we take an electron and positron, and have them orbit each other in a "binary" system, the positron would cause the electron potential to change based on whether the electron rotated or not while these particles orbited one another. And, Weinberg is saying, the reason I had you, Yablon, lay out these potentials, is because I knew that sooner or later you would get to the point with your fractional charges that I could shoot down this whole crazy idea by pointing out that for these fractional charges to exist as you claim they do, your monopole potential could not be independent of what you are putting into the potential, and nobody ever deals that way with a Coulomb potential, electric or magnetic. End of story.
magnetic monopole potential is full strength when there is no tidal lock, but is half strength when there is a tidal lock? In order for that to happen, the potential of the monopole would have to be dependent on the wavefunction itself, rather than independent of the detecting wavefunction. And we know very well -- at least in classical electrodynamics -- that subject of course to choosing a "ground" which we handle formally through gauge symmetry, the potential is the potential, and whatever particles you run through that potential do not charge the potential, except insofar as those objects generate their own potentials. Further, nobody would ever contend that if we take an electron and positron, and have them orbit each other in a "binary" system, the positron would cause the electron potential to change based on whether the electron rotated or not while these particles orbited one another. And, Weinberg is saying, the reason I had you, Yablon, lay out these potentials, is because I knew that sooner or later you would get to the point with your fractional charges that I could shoot down this whole crazy idea by pointing out that for these fractional charges to exist as you claim they do, your monopole potential could not be independent of what you are putting into the potential, and nobody ever deals that way with a Coulomb potential, electric or magnetic. End of story.
This is actually a very good argument, showing that Weinberg was looking at the chessboard several moves ahead, and in classical electrodynamics, it cannot be refuted. But now let's talk about quantum electrodynamics. For my fractional charges to remain viable in light of the above, it would be necessary for the monopole potentials to in fact change based on how one detects them. These monopoles would have to be objects having the quantum behavior whereby the very act of observing changes what is observed. So the very act of detecting the monopole with a tidally-locked wavefunction rather than one which is not tidally locked has the wavefunction interacting with the monopole so as to change the quantum state of the monopole from one with a full-strength to one with a half-strength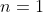 potential. That is, the tidally-locked wavefunction has to interact with the magnetic monopole with sufficient strength over a wavefunction not in a tidal lock, so as to literally kick the monopole into a different quantum state with a half-strength potential. This, I believe, is exactly what is happening, in physical reality. And in fact, the way in which Weinberg has rather cleverly forced me to look at this starting with explicitly laying out the the monopole potentials actually strengthens my view and the support I can bring to my view that these half integer monopole charges (and the odd-integer fractional monopole charges to which these are a waystation) are in fact what is being observed in the Fractional Quantum Hall Effect (FQHE) near absolute zero. Below, I will briefly explain how all of these puzzle pieces fit together. I am as it happens already writing all of this up; so this fits very well with what I am already doing and seeing. For now, I will simply state the theory in broadest terms. I will share this with greater supporting detail in the coming days and weeks.
potential. That is, the tidally-locked wavefunction has to interact with the magnetic monopole with sufficient strength over a wavefunction not in a tidal lock, so as to literally kick the monopole into a different quantum state with a half-strength potential. This, I believe, is exactly what is happening, in physical reality. And in fact, the way in which Weinberg has rather cleverly forced me to look at this starting with explicitly laying out the the monopole potentials actually strengthens my view and the support I can bring to my view that these half integer monopole charges (and the odd-integer fractional monopole charges to which these are a waystation) are in fact what is being observed in the Fractional Quantum Hall Effect (FQHE) near absolute zero. Below, I will briefly explain how all of these puzzle pieces fit together. I am as it happens already writing all of this up; so this fits very well with what I am already doing and seeing. For now, I will simply state the theory in broadest terms. I will share this with greater supporting detail in the coming days and weeks.
As I have been maintaining and developing for what is now just over a year, at ultra low-temperatures near 0K, Dirac monopoles come into existence, and there is a formal duality symmetry under the interchange of the electric and magnetic charge strengths coming very clearly out of the standard Dirac condition known since 1931, derived at (4.7) of my paper:
duality symmetry under the interchange of the electric and magnetic charge strengths coming very clearly out of the standard Dirac condition known since 1931, derived at (4.7) of my paper:
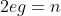 (4.7)
(4.7)
This is the single most important symmetry to be found at low temperatures, and although this is not yet understood or accepted by the wider physics community, it is at the heart of all of the very unusual electromagnetic phenomena which are observed in condensed matter physics when one freezes a conductive "host material" down to near 0K and then starts generating currents (superconductivity) or applying very strong magnetic fields (FQHE) while measuring what is going on. It is also helpful to think about this the other way: near 0K magnetic monopoles really do exist and lie at the root of all the unusual electrodynamics and particularly magnetic behaviors seen at those temperatures in condensed matter physics. Then, when we start to add some heat to bring the temperatures up to a few degrees Kelvin (exact temperatures being dependent on the particular host material), the monopoles melt (and in fact melt into a "thermal residue charge" which is at the heart of the partition functions used in thermodynamics leading to a direct unification between electrodynamics and thermodynamics which writing up will be my major winter project this year), and the duality symmetry disappears / becomes hidden, not to be seen again until one gets up to the ultra-high GUT energies of the early universe where 't Hooft and Polyakov and most everybody else have been looking for magnetic monopoles. Indeed, those who have studied my posts here know that I have said for several years that the road to the unification of all of physics is paved with magnetic monopoles. Up until a year ago I spent several years showing how baryons are themselves the topologically-stable magnetic monopoles of Yang-Mills theory following spontaneous symmetry breaking, and used this to explain the binding energies of fifteen (15) light nuclides from isotopes of hydrogen through nitrogen to parts per million relative to observational data, and to explain the proton and neutron masses in relation to very precisely-specified quark masses within all known experimental errors.
duality symmetry disappears / becomes hidden, not to be seen again until one gets up to the ultra-high GUT energies of the early universe where 't Hooft and Polyakov and most everybody else have been looking for magnetic monopoles. Indeed, those who have studied my posts here know that I have said for several years that the road to the unification of all of physics is paved with magnetic monopoles. Up until a year ago I spent several years showing how baryons are themselves the topologically-stable magnetic monopoles of Yang-Mills theory following spontaneous symmetry breaking, and used this to explain the binding energies of fifteen (15) light nuclides from isotopes of hydrogen through nitrogen to parts per million relative to observational data, and to explain the proton and neutron masses in relation to very precisely-specified quark masses within all known experimental errors.
But let's get back to_{em}) monopoles and the tidal lock business. Dirac was also the first to point out that although his monopoles possessed a
monopoles and the tidal lock business. Dirac was also the first to point out that although his monopoles possessed a  duality symmetry, this was not a complete symmetry owing to the relatively weak strength of the electric charge
duality symmetry, this was not a complete symmetry owing to the relatively weak strength of the electric charge  . Indeed, using the fine structure constant
. Indeed, using the fine structure constant  , Dirac pointed out that the magnetic force between poles would be larger than the electric force by a factor of "
, Dirac pointed out that the magnetic force between poles would be larger than the electric force by a factor of "^2=4692)
 ." So, near 0K where these monopole do exist, there will be extremely strong forces at work that evaporate just a few degrees above 0K, the precise temperature being material dependent. And what does this have to do with tidal locks? In classical physics -- think gravitation and the Riemann curvature tensor -- a tidal lock occurs when two bodies are "attracting" one another (really, the geometry is curved) so strongly as to break any perfect sphere one may mentally attribute to those bodies, and instead produce a mild or even severe bulge in one or both of the bodies along their axis of separation. The bulge, in turn, combines with the attractive "force" (really, pursuit of a geodesic path through the geometry by each infinitesimal piece of the bodies) to constrain any independent rotation of one or both bodies, and force them into a tidal lock, such as what happens to the moon in its earth orbit, aside from the libration owing to this orbit being mildly eccentric and not perfectly circular. But it is a strong "attractive" "force" which is responsible for the bulge which in turn locks in the synchronous rotation. So, back to Dirac monopoles: When the temperature approaches 0K, what at higher temperatures were simple electrons now "condense" into magnetic monopoles containing a magnetic charge that will interact with another magnetic charges 4692.25 times as strongly as the electric charges interact among themselves. So while electric charges alone could get an electron and a positron to interact, they are not yet strong enough to put them into a tidal lock. But when the temperature is cooled to near 0K and some of the electrons start to "go magnetic," the forces between opposite magnetic charges become sufficiently large to in fact produce a tidal lock. And the tidal lock produces half-integer charges as in (5.16) above. Then, when the temperature is raised and the magnetic charges melt into thermal charges that drive the partition functions of thermodynamics leading to thermodynamics as we know and observe it, all that is left are electrons without their stronger-by-4692.25 magnetic charges, there are no longer any tidal locks, and so the only thing we now observe are whole-integer charges of Thompson and Millikan with the whole-integer condition (4.12) which is responsible for the observed quantization of electric charge via the thermal residue from the magnetic charge which unifies electrodynamics and thermodynamics.
." So, near 0K where these monopole do exist, there will be extremely strong forces at work that evaporate just a few degrees above 0K, the precise temperature being material dependent. And what does this have to do with tidal locks? In classical physics -- think gravitation and the Riemann curvature tensor -- a tidal lock occurs when two bodies are "attracting" one another (really, the geometry is curved) so strongly as to break any perfect sphere one may mentally attribute to those bodies, and instead produce a mild or even severe bulge in one or both of the bodies along their axis of separation. The bulge, in turn, combines with the attractive "force" (really, pursuit of a geodesic path through the geometry by each infinitesimal piece of the bodies) to constrain any independent rotation of one or both bodies, and force them into a tidal lock, such as what happens to the moon in its earth orbit, aside from the libration owing to this orbit being mildly eccentric and not perfectly circular. But it is a strong "attractive" "force" which is responsible for the bulge which in turn locks in the synchronous rotation. So, back to Dirac monopoles: When the temperature approaches 0K, what at higher temperatures were simple electrons now "condense" into magnetic monopoles containing a magnetic charge that will interact with another magnetic charges 4692.25 times as strongly as the electric charges interact among themselves. So while electric charges alone could get an electron and a positron to interact, they are not yet strong enough to put them into a tidal lock. But when the temperature is cooled to near 0K and some of the electrons start to "go magnetic," the forces between opposite magnetic charges become sufficiently large to in fact produce a tidal lock. And the tidal lock produces half-integer charges as in (5.16) above. Then, when the temperature is raised and the magnetic charges melt into thermal charges that drive the partition functions of thermodynamics leading to thermodynamics as we know and observe it, all that is left are electrons without their stronger-by-4692.25 magnetic charges, there are no longer any tidal locks, and so the only thing we now observe are whole-integer charges of Thompson and Millikan with the whole-integer condition (4.12) which is responsible for the observed quantization of electric charge via the thermal residue from the magnetic charge which unifies electrodynamics and thermodynamics.
So now, how do I reply to Weinberg's perfectly correct classical position? We must focus on the fermion wavefunction itself which is doing the detection of the magnetic monopole. If the wavefunction is truly physically tidally locked to a magnetic monopole, then the wavefunction must itself be the wavefunction for an electron that has "gone magnetic," and so possesses the magnetic charge that will enable it to get into a tidal lock with the monopole. That is, the only wavefunction which will tidally lock to a magnetic monopole, is a wavefunction for another magnetic monopole. If the wavefunction is not tidally locked to the monopole, then the wavefunction is necessarily that of an ordinary electron which has not "gone magnetic." And as a consequence, all that will be detected is the integer charge condition. So, going back to the quantum maxim that the act of observing changes that which is being observed, the reason what a wavefunction in a tidal lock with a magnetic monopole can and does kick the potential for the magnetic monopole into a different quantized state, is because that wavefunction itself must be for an electron which has itself condensed into a second magnetic monopole (of opposite charge), and so is the wavefunction for a different particle than that of an ordinary electron. So, in answer to Weinberg, yes, a tidally-locked electron wavefunction will kick the magnetic monopole potential into a different, half-integer quantum state, because by being in a tidal lock, that electron is no longer an ordinary electron, but is itself a second magnetic monopole with a charge that interacts 137/2 times as strongly as the electric charge, that then in turn does indeed cause the potential of the first monopole to move into a different quantum state. When you have a magnetic monopole interacting with an ordinary electron, the forces between them are not strong enough to create a tidal lock, so the monopole has the potential (4.12). When that same monopole interacts with an electron that has condensed into another magnetic monopole due to sufficient cooling, then that second monopole kicks the first monopole potential into (5.16), and more precisely, both monopoles go into a tidal lock and cause one another to assume the potentials (5.16). And that is where the quantum theory overcomes the classical theory when it comes to magnetic monopoles. At the same time, this leads to some very strong pair production, and this is witnessed through so-called Cooper pairing of condensed matter physics. Further, because any pair of fermions locking together will exhibit the spin characteristics of a boson, all of this gets us in the downstream development to be able to correlate spins and atomic orbital shells (characterized by total angular momentum) with fractional charge states, which will be a primary vehicle I will use to propose "spin-charge correlation" experiments that will confirm all of this.
I am looking for a good name for these electrons that have "gone magnetic." For the moment, I am calling them "magneto-electrons." So in these terms, only magneto-electrons can tidally lock together, and when they do, the strong forces between them kick them into having the half-integer quantized potentials (5.16). But when an ordinary electron interacts with a magneto-electron, the forces are not strong enough for a tidal lock, and consequently, nor are they strong enough to kick the monopole potential from (4.12) into (5.16). And that is how I answer Weinberg's perfectly-correct classical critique, which no longer holds up in the quantum world of electrons that condense at low temperatures into magnetic monopoles which are responsible for all of the unusual E&M behaviors seen in condensed matter physics. And if low temperatures cause electromagnetic charges and potentials to quantize differently, then there is also a fundamental unification of electrodynamics and thermodynamics sitting right in the middle of all this. Again, writing this up will be my major winter project this year. Not end of story!
Jay
PRD explanation wrote:Your paper was rejected because it is wrong. In order to avoid any confusions arising from the properties of spinors, I cited the example of a spinless charged particle. In response, you present a claim that such a particle would not detect a half-integer monopole. This is certainly implausible: A magnetic monopole, by definition, creates a Coulomb magnetic field. Any charged particle will certainly be affected by this magnetic field (e.g., by a Lorentz force if the particle is moving), regardless of the source of that field. The standard Dirac arguments then lead to the conclusion that such a particle will detect a singularity unless the charge of the monopole satisfies the Dirac quantization condition.
In reply I wrote back:
Yablon reply to PRD wrote:Thank you for your email of 12:38 PM today. All I really wanted was an explanation of why you had concluded that my reply was unpersuasive, and not simply a statement that it was. You provided that today, and I will now take that under advisement in a positive way. Because you have now explained why you reached your conclusion, I see no need to pursue an appeal, and so you may keep this paper inactive.
Now let's talk about the physics of all of this. I will refer to the latest draft of my paper posted at http://vixra.org/pdf/1511.0151v2.pdf. I also want to thank guest1202 for another insightful recent post, I will get to that separately when I have a chance.
First, with this rejection, I understand the longer-term method to Weinberg's madness. He is the one who when rejecting a draft early in 2015 suggested that I explicitly derive the potentials for the Dirac magnetic monopoles as well as whatever fractional monopoles I was pursuing. I did so for the usual Dirac monopoles at (4.12), namely:
This potential is well known, see for example, the final set-off equation at https://www.encyclopediaofmath.org/inde ... c_monopole, which is a very good reference that I urge you to read if you are trying to follow this thread. Note that I use a reversed sign convention from this reference. No tidal lock in (4.12).
Following suit, at (5.16) I set out the monopole potential for a wavefunction which is in a tidal lock, namely:
This is associated with my claimed half-integer Dirac monopole charges. It is easily seen that the
So here is what Weinberg is really saying, and in classical physics it is a perfectly correct argument: Equations (4.12) and (5.16) are both the equations for the electromagnetic vector potential one-form of a magnetic monopole. What you, Yablon, are telling me, is that if you detect the monopole with an electron that is not tidally locked, you get the potential (4.12). But then, if you detect the same monopole with an electron that is tidally locked, you get the different potential (5.16). But these potentials belong to the monopole itself. They should not depend on what you put into the potential to detect things. Further, the potential will of course determine the motions of electrons and other charged particles placed in that potential, because at the end of the day the magnetic monopole -- as unusual an object as it might be were it to exist -- is still creating a magnetic field indistinguishable from any ordinary magnetic field other than the fact that it has a monopolar field configuration, and we know from Maxwell and Lorentz how a charged particle will behave in a magnetic field. E&M 101. So how can you tell me that I can take an electron wavefunction, and have it respond as if the
This is actually a very good argument, showing that Weinberg was looking at the chessboard several moves ahead, and in classical electrodynamics, it cannot be refuted. But now let's talk about quantum electrodynamics. For my fractional charges to remain viable in light of the above, it would be necessary for the monopole potentials to in fact change based on how one detects them. These monopoles would have to be objects having the quantum behavior whereby the very act of observing changes what is observed. So the very act of detecting the monopole with a tidally-locked wavefunction rather than one which is not tidally locked has the wavefunction interacting with the monopole so as to change the quantum state of the monopole from one with a full-strength to one with a half-strength
As I have been maintaining and developing for what is now just over a year, at ultra low-temperatures near 0K, Dirac monopoles come into existence, and there is a formal
This is the single most important symmetry to be found at low temperatures, and although this is not yet understood or accepted by the wider physics community, it is at the heart of all of the very unusual electromagnetic phenomena which are observed in condensed matter physics when one freezes a conductive "host material" down to near 0K and then starts generating currents (superconductivity) or applying very strong magnetic fields (FQHE) while measuring what is going on. It is also helpful to think about this the other way: near 0K magnetic monopoles really do exist and lie at the root of all the unusual electrodynamics and particularly magnetic behaviors seen at those temperatures in condensed matter physics. Then, when we start to add some heat to bring the temperatures up to a few degrees Kelvin (exact temperatures being dependent on the particular host material), the monopoles melt (and in fact melt into a "thermal residue charge" which is at the heart of the partition functions used in thermodynamics leading to a direct unification between electrodynamics and thermodynamics which writing up will be my major winter project this year), and the
But let's get back to
So now, how do I reply to Weinberg's perfectly correct classical position? We must focus on the fermion wavefunction itself which is doing the detection of the magnetic monopole. If the wavefunction is truly physically tidally locked to a magnetic monopole, then the wavefunction must itself be the wavefunction for an electron that has "gone magnetic," and so possesses the magnetic charge that will enable it to get into a tidal lock with the monopole. That is, the only wavefunction which will tidally lock to a magnetic monopole, is a wavefunction for another magnetic monopole. If the wavefunction is not tidally locked to the monopole, then the wavefunction is necessarily that of an ordinary electron which has not "gone magnetic." And as a consequence, all that will be detected is the integer charge condition. So, going back to the quantum maxim that the act of observing changes that which is being observed, the reason what a wavefunction in a tidal lock with a magnetic monopole can and does kick the potential for the magnetic monopole into a different quantized state, is because that wavefunction itself must be for an electron which has itself condensed into a second magnetic monopole (of opposite charge), and so is the wavefunction for a different particle than that of an ordinary electron. So, in answer to Weinberg, yes, a tidally-locked electron wavefunction will kick the magnetic monopole potential into a different, half-integer quantum state, because by being in a tidal lock, that electron is no longer an ordinary electron, but is itself a second magnetic monopole with a charge that interacts 137/2 times as strongly as the electric charge, that then in turn does indeed cause the potential of the first monopole to move into a different quantum state. When you have a magnetic monopole interacting with an ordinary electron, the forces between them are not strong enough to create a tidal lock, so the monopole has the potential (4.12). When that same monopole interacts with an electron that has condensed into another magnetic monopole due to sufficient cooling, then that second monopole kicks the first monopole potential into (5.16), and more precisely, both monopoles go into a tidal lock and cause one another to assume the potentials (5.16). And that is where the quantum theory overcomes the classical theory when it comes to magnetic monopoles. At the same time, this leads to some very strong pair production, and this is witnessed through so-called Cooper pairing of condensed matter physics. Further, because any pair of fermions locking together will exhibit the spin characteristics of a boson, all of this gets us in the downstream development to be able to correlate spins and atomic orbital shells (characterized by total angular momentum) with fractional charge states, which will be a primary vehicle I will use to propose "spin-charge correlation" experiments that will confirm all of this.
I am looking for a good name for these electrons that have "gone magnetic." For the moment, I am calling them "magneto-electrons." So in these terms, only magneto-electrons can tidally lock together, and when they do, the strong forces between them kick them into having the half-integer quantized potentials (5.16). But when an ordinary electron interacts with a magneto-electron, the forces are not strong enough for a tidal lock, and consequently, nor are they strong enough to kick the monopole potential from (4.12) into (5.16). And that is how I answer Weinberg's perfectly-correct classical critique, which no longer holds up in the quantum world of electrons that condense at low temperatures into magnetic monopoles which are responsible for all of the unusual E&M behaviors seen in condensed matter physics. And if low temperatures cause electromagnetic charges and potentials to quantize differently, then there is also a fundamental unification of electrodynamics and thermodynamics sitting right in the middle of all this. Again, writing this up will be my major winter project this year. Not end of story!
Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Jay
Exciting posts! Glad you have made progress with the feedback.
At normal temperature, for a hydrogen atom, with one electron and one proton, the electron is not tidally locked to a proton (magnetic monopole)? Or is the proton only a magnetic monopole at zero temperature? The photon [which has no net electric charge] is the [electric] force boson exchanged between the electron and a quark from the proton.
At zero degrees K, presumably, the electron could/would be tidally locked with the proton (which is now definitely a magnetic monopole). There may be changes to the nature of the electron which require it to have a new name, as you say, as the electron has different properties at 0K. Does the proton (or its quarks) need a new name at 0K, other than the generic name 'magnetic monopole'? Is the photon still the force boson between the magneto-electron and the proton/magnetic monopole, but say being exchanged much more frequently? You mentioned a strong force but I do not think you meant the QCD strong force? (Sorry, I should be able to remember that from your paper.) Though at 0K the range of the gluon might possibly extend its effective range to include the electron tidally locked to the proton.
Exciting posts! Glad you have made progress with the feedback.
At normal temperature, for a hydrogen atom, with one electron and one proton, the electron is not tidally locked to a proton (magnetic monopole)? Or is the proton only a magnetic monopole at zero temperature? The photon [which has no net electric charge] is the [electric] force boson exchanged between the electron and a quark from the proton.
At zero degrees K, presumably, the electron could/would be tidally locked with the proton (which is now definitely a magnetic monopole). There may be changes to the nature of the electron which require it to have a new name, as you say, as the electron has different properties at 0K. Does the proton (or its quarks) need a new name at 0K, other than the generic name 'magnetic monopole'? Is the photon still the force boson between the magneto-electron and the proton/magnetic monopole, but say being exchanged much more frequently? You mentioned a strong force but I do not think you meant the QCD strong force? (Sorry, I should be able to remember that from your paper.) Though at 0K the range of the gluon might possibly extend its effective range to include the electron tidally locked to the proton.
- Ben6993
- Posts: 287
- Joined: Sun Feb 09, 2014 12:53 pm
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
Ben6993 wrote:Jay
Exciting posts! Glad you have made progress with the feedback.
At normal temperature, for a hydrogen atom, with one electron and one proton, the electron is not tidally locked to a proton (magnetic monopole)? Or is the proton only a magnetic monopole at zero temperature? The photon [which has no net electric charge] is the [electric] force boson exchanged between the electron and a quark from the proton.
At zero degrees K, presumably, the electron could/would be tidally locked with the proton (which is now definitely a magnetic monopole). There may be changes to the nature of the electron which require it to have a new name, as you say, as the electron has different properties at 0K. Does the proton (or its quarks) need a new name at 0K, other than the generic name 'magnetic monopole'? Is the photon still the force boson between the magneto-electron and the proton/magnetic monopole, but say being exchanged much more frequently? You mentioned a strong force but I do not think you meant the QCD strong force? (Sorry, I should be able to remember that from your paper.) Though at 0K the range of the gluon might possibly extend its effective range to include the electron tidally locked to the proton.
Hi Ben,
I knew I should have qualified the use of the word "strong" to make clear that I was talking about a strong electromagnetic force, and not about the strong force of nuclear physics. Two different things. Also, the magnetic monopoles I am talking about here are are true
In contrast, When I talk about Yang-Mills magnetic monopoles, and in the work I did prior to a year ago to obtain the binding energy results that you followed very closely, those monopoles are topologically-stable
So: when talking about low temperatures, get the protons and neutrons out of your mind. What I am doing presently is all about electrons and positrons and how these becomes Maxwellian magnetic monopoles near 0K and how their condensing into magnetic monopoles is what causes all of the unusual electromagnetic behaviors we see in condensed matter.
Now -- to be sure, and I have this in the back of my mind but have not developed it yet -- I may very well go back to my work on Yang-Mills monopoles some time later in 2016, and roll in what I am now doing for
So, I hope that gives some further context to what I am doing. But for the sake of understanding what I am presently writing about, do not at all think about protons and neutrons and strong interactions in the sense of QCD. Think about electrons only, and about them and their positron antiparticles becoming magnetic monopoles near 0K and interacting "strongly" with one another n the sense of a very "strong magnetic force" that is not the same as the "strong nuclear force." This is against the backdrop I have earlier developed of how the strong nuclear force itself is the force of attraction between Yang-Mills chromo-magnetic monopoles arising out of non-commuting, non-abelian gauge fields.
Jay
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
Re: Half-Integer Fractional Dirac Magnetic Monopole Charges
guest1202 wrote: Dirac's analysis was framed is a setting of standard quantum mechanics in which a "state" is a nonzero complex-valued square-integrable function on three-dimensional real Euclidean space R^3, with the important caveat:
TWO SUCH FUNCTIONS ARE CONSIDERED THE "SAME" IF EACH OF THEM IS A NONZERO COMPLEX SCALAR MULTIPLE OF THE OTHER .
Two functions psi and phi are considered as representing the "same" state if

for some nonzero complex constant c. Colloquially, phi is called a "wavefunction", and the caveat is ignored in talking about it. However, sometimes one can't ignore the caveat, and your cont is one of these times, as I shall try to explain below. In short, a "wavefunction" is not really a function, but is an equivalence class of functions related as just described. . . .{refer to original for the rest}
Good morning guest1202:
Let me begin my reply to your recent post. Since my time is very limited during the next couple of weeks, I will break up the reply and write as time permits. Here, I will discuss the point you raised in the quoted excerpt above.
It seems to me that the fundamental question here requires a close consideration of Max Born's requirement, often considered a tenet of quantum mechanics, that a wavefunction
Therefore, let us now consider a transformation
So this may lead someone to take the view that if we say "the wavefunction
Let me now again refer to https://www.encyclopediaofmath.org/inde ... c_monopole. Just before (a3) this article states: "The wave function
The requirement for a rigid rather than relaxed single-valued condition when dealing with a wavefunction in the field of a magnetic monopole originates from the fact that we are starting out with the wavefunction at an azimuth
To help in thinking about this, note that when we place a wavefunction near a magnetic monopole, we are placing it in a region of "curvature" in the gauge space, and in effect, engaging in a form of parallel transport. Why do I say this? The magnetic field B is among the components of the field strength two-form
Insofar as my half-integer charges and potentials are concerned, I am applying the same analysis as https://www.encyclopediaofmath.org/inde ... c_monopole. However, there is an extra minus sign that will end up in the unnumbered equation set out above (a3) if the wavefunction is in a tidal lock. We still maintain the rigid requirement for single valuedness, requiring the wavefunction orientation in the complex Euler space after the loop to end up pointing in the same direction it had pointed at the start of the loop. But when we do this, we get half-integer charges.
As Weinberg pointed out and as I elaborated in my post yesterday in this same topic discussion, this appears to lead to the "wrong" result that the vector potential of the monopole is affected by whether the wavefunction rotates or not in a tidal lock. As I argued yesterday, this is indeed a paradoxical result when viewed through the lens of classical electrodynamics. But from a quantum view, this is yet another example of how the act of detecting can induce a change in that which is being detected, and it is perfectly, physically possible.
More to follow on other aspects of your post, when time permits.
Jay
PS:
guest1202 wrote:Regarding your suggestion that I register as a member of this group, I prefer to remain anonymous because of the frequently toxic and insulting language of some of the regular posters, particularly regarding the discussion of Bell's inequalities. I don't want to be associated in any way with a group which tolerates such incivility.
If you wish to get in touch with me privately at any time, I invite you to please do so at yablon@alum.mit.edu.
- Yablon
- Independent Physics Researcher
- Posts: 365
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: New York
36 posts
• Page 1 of 2 • 1, 2
Return to Sci.Physics.Foundations
Who is online
Users browsing this forum: No registered users and 134 guests

