gill1109 wrote:OK, maybe I'm a bit old-fashioned. From here on, some old man's ramblings, connecting this all to the very important topic of old Dutch genever. Which I hope to enjoy with many of you when our Symposium and Workshop finally materialises. At which we will be able to admire, on a wall, the genuine and original signatures of Einstein, Lorentz and Ehrenfest.
I too look forward to all that. Let's keep trucking on to the symposium!
Two comments came in overnight, this one from Richard, and another from Heinera. I will reply to Richard here, then hopefully this evening after a busy day with my little grandson, to Heinera.
gill1109 wrote:Yablon wrote:7) Does anybody have any problem with connecting
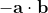
to a correlation as that term is defined in statistics, to arrive at:
=-\mathbf{a}\cdot \mathbf{b})
(1.20)
Jay: I need to know how you think that the term "correlation" is defined in "statistics" before I can make any comment on this statement.
I do have pretty firm ideas about what "statistics" is and how "correlation" is defined in statistics - I've been teaching statistics to mathematicians, economists, astronomers, and psychologists, and data-scientists, for 45 years.
Richard, I am glad you asked that question. And you are the ideal person to be asking that question given your first rate background in this area. Probably nobody except my own high school chums know or remember this, but in high school, I was allowed by the faculty to teach a course in probability and statistics which was attended by fellow students and even a few teachers. Indeed, my first mathematics love was probability and statistics. Done with this old man's ramblings and on to business.
It is my impression that many discussions of QM correlations focus on the
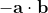
from QM reviewed in my most recent points 1-6 , but not sufficiently on why we can call this a correlation, the point 7 your cited. Is this some unique type of correlation developed for QM? Of course it is not. It is a correlation precisely as that term is used in statistics, and I felt it important, at least in anything I write, to not omit that point.
So, my detailed explanation is in (1.17) through (1.20) of
https://jayryablon.files.wordpress.com/ ... -4.1-1.pdf. Here, let me just review the main points:
We start with the standard statistics definition
=\text{cov}\left( X,Y \right)/\Delta \left( X \right)\Delta \left( Y \right))
where
=\left\langle XY \right\rangle -\left\langle X \right\rangle \left\langle Y \right\rangle)
, and the standard deviations are
=+\sqrt{\left\langle {{X}^{2}} \right\rangle -{{\left\langle X \right\rangle }^{2}}})
and
=+\sqrt{\left\langle {{Y}^{2}} \right\rangle -{{\left\langle Y \right\rangle }^{2}}})
. In sum, the correlation is a normalized covariance.
Because
\left( \sigma \cdot \mathbf{b} \right) \right\rangle =\mathbf{a}\cdot \mathbf{b})
, point 4, equation (1.15), we want to first calculate the correlation between
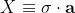
and
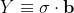
, by plugging these right into the statistical definitions.
This leads to:
=\frac{\operatorname{cov}\left( \sigma \cdot \mathbf{a},\sigma \cdot \mathbf{b} \right)}{\Delta \left( \sigma \cdot \mathbf{a} \right)\Delta \left( \sigma \cdot \mathbf{b} \right)}=\frac{\left\langle \left( \sigma \cdot \mathbf{a} \right)\left( \sigma \cdot \mathbf{b} \right) \right\rangle -\left\langle \sigma \cdot \mathbf{a} \right\rangle \left\langle \sigma \cdot \mathbf{b} \right\rangle }{\Delta \left( \sigma \cdot \mathbf{a} \right)\Delta \left( \sigma \cdot \mathbf{b} \right)})
(1.17a)
with the standard deviations:
=\sqrt{\left\langle {{\left( \sigma \cdot \mathbf{a} \right)}^{2}} \right\rangle -{{\left\langle \sigma \cdot \mathbf{a} \right\rangle }^{2}}}$)
=\sqrt{\left\langle {{\left( \sigma \cdot \mathbf{b} \right)}^{2}} \right\rangle -{{\left\langle \sigma \cdot \mathbf{b} \right\rangle }^{2}}}$)
(1.17b)
I know that you, Richard, raised the point to me privately whether you can actually plug the Hermitan matrices
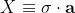
and
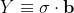
into the statistical formulas because they are matrices not random variables. But, if you look at (1.17), the only real question is whether each expression inside (1.17) has definite mathematical meaning for these matrices. And if you inspect closely you will see that they do. I discuss this in more detail in the paper draft.
So when we do the calculations and include a minus sign in front of
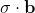
, we end up with:
=-\left\langle \left( \sigma \cdot \mathbf{a} \right)\left( \sigma \cdot \mathbf{b} \right) \right\rangle =-\mathbf{a}\cdot \mathbf{b})
(1.19)
Finally, we make the
definition:
\equiv \text{corr}\left( \sigma \cdot \mathbf{a},-\sigma \cdot \mathbf{b} \right)=-\mathbf{a}\cdot \mathbf{b})
(1.20)
recognizing that the minus sign is attributable not to the orientation of the Alice and Bob detectors, but to the oppositely-oriented angular momenta emerging in the two particles which split off out of each singlet prepared state.
Jay
So I am exhausted. I do want to pick up on Heinera's question regarding hidden variables, but will need to do so when I am fresh in the morning.