 by Yablon » Fri Mar 04, 2016 3:10 pm
by Yablon » Fri Mar 04, 2016 3:10 pm
To all:
The reply below was sent along privately from a person who does not want to directly participate in the public discussions. So I am providing that reply here without that person's identity.
I have had a chance to analyze what our anonymous guest is saying. He is right about the error in (6.12), and that has been there since the late December draft where he did not see the error but it was there.
In fact, when I originally did the Lorentz force derivation, I thought this would add an extra term to the Lorentz force law, but because of the "zero" he said is wrong which is wrong, I did not have this extra term in there. But this person did correctly pinpoint the part of the derivation that gave me the most agita originally, so I was indeed happy that someone dug deeply enough the ferret this out and not surprised that this is where he focused.
Consequently, there IS an extra term in the Lorentz force that I have been neglecting. However, apropos to his other point about the potentials, I can gauge that extra term out as unobservable, and so get that term to zero by a different route and still have the Lorentz force law intact. So we live to fight another day, as they say!

I will post a draft with the updated details of this over the weekend.
One other point in reply: the metric tensor
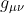
, like the gauge potential
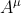
, is also not unique because it too is subject to a symmetric gauge transformation using the local vector parameter

in the combination

. But this does not bar us from having this gauge-able gravitational potential in the expression for the metric interval
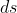
nor does it ruin the invariant meaning of this interval.
Jay
anonymous guest wrote:Dear Mr. Yablon,
I tried several times to download the latest 140-page version of your paper "On the Geometric Foundations of Classical Electrodynamics", but every time the same thing happened: After few hundred kilobytes downloaded, the download failed because of an unspecified "network error". Previously, I had successfully downloaded the January 26 42-page version, so the following comments will refer to that version.
I think there is a serious mistake (actually, several) in its equation (6.12), which invalidates the paper's main claim that its methods imply a geometric derivation of the general relativistic equation of motion for a classical charged particle. Following is (6.12):
 \delta x^\alpha \, ds = \int_A^B \frac{\partial \ }{\partial x^\alpha} (A_\sigma A^\sigma) \delta x^\alpha ds = \left. \frac{ds}{dx^\alpha} (A_\sigma A^\sigma) \delta x^\alpha \right|^A_B = 0 \quad .)
First of all, I question the passage from
 \delta x^\alpha ds)
to
 \delta x^\alpha \right|^A_B)
. It looks as if you transferred the dummy integration symbol
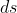
to the "numerator" of the differential operator

, but this would not be legitimate. Even if it were legitimate, the next equation ("

") would not follow.
The reason that I think that this is an error rather than my inability to guess the reasons for the steps is that I think the following is an actual counterexample to (6.12). Consider
any potential
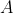
in Minkowski space for which
 > 0)
and
 =0)
for spatial indices

. For example,
 := x^0)
with

for

. If you want to make
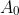
bounded with compact support, (which is often implicitly assumed in physics discussions), cut it off to make it bounded and smooth appropriately. Then the integral on the left of (6.12) becomes
^2)\delta x^0 \, ds)
which clearly will not vanish for
all variations
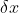
satisfying the variational boundary conditions
 = \delta x^0 (A) = 0)
.
It may save you some aggravation to carefully examine 6.12) before submitting the paper. Regardless of its merits, it will almost certainly be rejected anyway because of its length, but the rejection may be for some spurious pretext. I would be surprised if most referees would read it carefully enough to spot the error in (6.12).
An earlier December 30 version obtains by another method the usual Lorentz equation in curved spacetime. I didn't notice any error in the earlier version, though I haven't tried to check it carefully. You could revert to that earlier
method, but I don't think it would be worth the effort for the following reasons.
Personally, I don't consider either method to be either "geometric", or a "derivation" which provides any fundamental insight. (I have the same opinion about the much-discussed Kaluza-Klein (KK) "derivation", so clearly my view is not generally accepted; you are in good company!) The reason is that both your new metrics and KK's involve the 4-potential A, which (classically) is considered to be unobservable. That is because it is not unique --- if one potential yields the field tensor F, then adding to it the (four-dimensional) gradient of a function gives another potential which yields the same F.
So, the potential is not like the quantities associated with Einstein's metric such as the proper time along a worldline. You can measure the proper time by carrying a clock, but there is no instrument which can measure the electromagnetic potential.
I can't see how writing down a mathematical expression such as a Lagrangian (which is basically the starting point for your December 30 version) and finding the equation of motion which extremizes it provides any physical insight. It seems to me to be just sterile calculation. One chooses the Lagrangian to obtain the equation of motion that one believes to be physically correct. If one doesn't already know the physically correct equation, guessing a Lagrangian and deriving one doesn't yield an equation on which one would confidently bet!
Your January 26 version well illustrates this. Its Lagrangian-like expression is a reasonable thing to try, but it yields the wrong equation of motion (after correcting the errors). The Lagrangian that the Dec. 30 version uses (which incidentally is well known and essentially in every electromagnetic text which discusses Lagrangians) does yield the correct equations, but is no more well-motivated than the Jan. 26 Lagrangian.
Before closing, I'd like to say that I am sorry the tone of the above is necessarily negative, because it deals with mistakes. I did find interesting things in your paper, such as the discussion of how electromagnetic forces may prevent someone standing on the earth from falling through it. I had never thought of that! I don't know if your explanation is correct (because the classical picture of an atom as a nucleus orbited by electrons is just a picture not well supported by quantum mechanics), but it provides food for thought. I am taking the time to write this in the hope that it may give you food for thought, in return for that which you have given me. Thank you!
To all:
The reply below was sent along privately from a person who does not want to directly participate in the public discussions. So I am providing that reply here without that person's identity.
I have had a chance to analyze what our anonymous guest is saying. He is right about the error in (6.12), and that has been there since the late December draft where he did not see the error but it was there.
In fact, when I originally did the Lorentz force derivation, I thought this would add an extra term to the Lorentz force law, but because of the "zero" he said is wrong which is wrong, I did not have this extra term in there. But this person did correctly pinpoint the part of the derivation that gave me the most agita originally, so I was indeed happy that someone dug deeply enough the ferret this out and not surprised that this is where he focused.
Consequently, there IS an extra term in the Lorentz force that I have been neglecting. However, apropos to his other point about the potentials, I can gauge that extra term out as unobservable, and so get that term to zero by a different route and still have the Lorentz force law intact. So we live to fight another day, as they say! ;) I will post a draft with the updated details of this over the weekend.
One other point in reply: the metric tensor [tex]g_{\mu\nu}[/tex], like the gauge potential [tex]A^\mu[/tex], is also not unique because it too is subject to a symmetric gauge transformation using the local vector parameter [tex]\Lambda_\mu[/tex] in the combination [tex]\partial_\mu \Lambda_\nu + \partial_\nu \Lambda_\mu[/tex]. But this does not bar us from having this gauge-able gravitational potential in the expression for the metric interval [tex]ds[/tex] nor does it ruin the invariant meaning of this interval.
Jay
[quote="anonymous guest"]Dear Mr. Yablon,
I tried several times to download the latest 140-page version of your paper "On the Geometric Foundations of Classical Electrodynamics", but every time the same thing happened: After few hundred kilobytes downloaded, the download failed because of an unspecified "network error". Previously, I had successfully downloaded the January 26 42-page version, so the following comments will refer to that version.
I think there is a serious mistake (actually, several) in its equation (6.12), which invalidates the paper's main claim that its methods imply a geometric derivation of the general relativistic equation of motion for a classical charged particle. Following is (6.12):
[tex]\int_A^B \partial_\alpha (A_\sigma A^\sigma) \delta x^\alpha \, ds = \int_A^B \frac{\partial \ }{\partial x^\alpha} (A_\sigma A^\sigma) \delta x^\alpha ds = \left. \frac{ds}{dx^\alpha} (A_\sigma A^\sigma) \delta x^\alpha \right|^A_B = 0 \quad .[/tex]
First of all, I question the passage from [tex]\int_A^B \frac{\partial \ }{\partial x^\alpha} (A_\sigma A^\sigma) \delta x^\alpha ds[/tex] to [tex]\left. \frac{ds}{dx^\alpha} (A_\sigma A^\sigma) \delta x^\alpha \right|^A_B[/tex] . It looks as if you transferred the dummy integration symbol [tex]ds[/tex] to the "numerator" of the differential operator [tex]\frac{\partial \ }{\partial x^\alpha}[/tex] , but this would not be legitimate. Even if it were legitimate, the next equation (" [tex]=0[/tex]") would not follow.
The reason that I think that this is an error rather than my inability to guess the reasons for the steps is that I think the following is an actual counterexample to (6.12). Consider [i]any[/i] potential [tex]A[/tex] in Minkowski space for which [tex]\partial_0 (A_\sigma A^\sigma) > 0[/tex] and [tex]\partial_i (A_\sigma A^\sigma) =0[/tex] for spatial indices [tex]i = 1, 2, 3.[/tex]. For example, [tex]A_0 (x^0, x^1, x^2, x^3) := x^0[/tex] with [tex]A_i \equiv 0[/tex] for [tex]i = 1,2,3[/tex]. If you want to make [tex]A_0[/tex] bounded with compact support, (which is often implicitly assumed in physics discussions), cut it off to make it bounded and smooth appropriately. Then the integral on the left of (6.12) becomes
[tex]\int_A^B \partial_0 ((A_0)^2)\delta x^0 \, ds[/tex]
which clearly will not vanish for [i]all[/i] variations [tex]\delta x[/tex] satisfying the variational boundary conditions [tex]\delta x^0 (B) = \delta x^0 (A) = 0[/tex].
It may save you some aggravation to carefully examine 6.12) before submitting the paper. Regardless of its merits, it will almost certainly be rejected anyway because of its length, but the rejection may be for some spurious pretext. I would be surprised if most referees would read it carefully enough to spot the error in (6.12).
An earlier December 30 version obtains by another method the usual Lorentz equation in curved spacetime. I didn't notice any error in the earlier version, though I haven't tried to check it carefully. You could revert to that earlier
method, but I don't think it would be worth the effort for the following reasons.
Personally, I don't consider either method to be either "geometric", or a "derivation" which provides any fundamental insight. (I have the same opinion about the much-discussed Kaluza-Klein (KK) "derivation", so clearly my view is not generally accepted; you are in good company!) The reason is that both your new metrics and KK's involve the 4-potential A, which (classically) is considered to be unobservable. That is because it is not unique --- if one potential yields the field tensor F, then adding to it the (four-dimensional) gradient of a function gives another potential which yields the same F.
So, the potential is not like the quantities associated with Einstein's metric such as the proper time along a worldline. You can measure the proper time by carrying a clock, but there is no instrument which can measure the electromagnetic potential.
I can't see how writing down a mathematical expression such as a Lagrangian (which is basically the starting point for your December 30 version) and finding the equation of motion which extremizes it provides any physical insight. It seems to me to be just sterile calculation. One chooses the Lagrangian to obtain the equation of motion that one believes to be physically correct. If one doesn't already know the physically correct equation, guessing a Lagrangian and deriving one doesn't yield an equation on which one would confidently bet!
Your January 26 version well illustrates this. Its Lagrangian-like expression is a reasonable thing to try, but it yields the wrong equation of motion (after correcting the errors). The Lagrangian that the Dec. 30 version uses (which incidentally is well known and essentially in every electromagnetic text which discusses Lagrangians) does yield the correct equations, but is no more well-motivated than the Jan. 26 Lagrangian.
Before closing, I'd like to say that I am sorry the tone of the above is necessarily negative, because it deals with mistakes. I did find interesting things in your paper, such as the discussion of how electromagnetic forces may prevent someone standing on the earth from falling through it. I had never thought of that! I don't know if your explanation is correct (because the classical picture of an atom as a nucleus orbited by electrons is just a picture not well supported by quantum mechanics), but it provides food for thought. I am taking the time to write this in the hope that it may give you food for thought, in return for that which you have given me. Thank you![/quote]
