The Geometrodynamic Foundation of Electrodynamics

[Yablon]

Hello to all:

This is an interim report on the paper I am developing based on may having found two months ago how to derive the Lorentz force law from minimizing the geodesic variation. You may view the present draft of this paper - which is turning into a book -- at the link below:

https://jayryablon.files.wordpress.com/ ... -1-spf.pdf

Sections 1-13 and 15 and 17 are substantially in complete and final form. Sections 14 and 16 are in progress and have equation notes. I intend in these sections to formally tie the non-linear behaviors of of electrodynamics for very strong interactions to the electron magnetic moment. That is why you will see some Dirac spinors thrown in there. Section 18 contains a document I wrote to this group in late December abut Kaluza-Klein that I will clean up and incorporate.

As to my last 2-3 weeks, it was pointed out to me privately by an active participant in this group that I should derive the geodesic deviation associated with all that I am doing, because this is the direct observable manifestation of spacetime curvature, and if I want this work to be accepted at the most serious level, I would have to be able to develop this and show that it fits with what is known and accepted in this arena. So I have been eyeballs deep in geodesic deviation and tidal forces and torques these past two weeks or so. Virtually all I have done in these past couple of weeks is in this part of the paper. Specifically:

Section 19 contains what was a somewhat challenging but I believe now-perfected derivation of the geodesic deviation. Section 20 contains the derivation of tidal forces for both Newtonian gravitation and Coulomb electrostatics. The validity of the later is indicated by its parallelism to the former. Section 21 derives the gravitational and electrostatic tidal torques, and then contains two of the most mathematically-difficult derivations I have ever done. First, the derivation of the simultaneous differential equations (21.19) for what is effectively the motion of gyroscopes subjected to gravitational and electrostatic tidal forces. Second, even harder, was the exact solution to these differential equations for a uniform charge distribution and constant radial distance between source and the mass or charge being acted upon by the source, for a spherical gyroscope (which is qualitatively illustrative of other shapes). That result is (21.31).

Then, just the past two days, I had to figure out what this solution really means, because I am not in a spaceship. So if you want to learn about interplanetary and interstellar navigation, read then end of section 21 and all of section 22. I plan to examine briefly how things change when the charge distribution is not uniform, and then to conclude this part of the paper with a whole section devoted to the Riemann curvature tensor and the electromagnetic field strength and curvature and time dilation in spacetime to seal the deal that what I am doing truly is correct and observable physics.

Finally, if we are deriving the Lorentz Force law from a variation based on what is really the Klein-Gordon equation, then we should be able to derive an analogous equation of motion from Dirac's equation as well. Individual spinors, of course, have a somewhat different motion than collections of charges, and this is how we explain atomic and nuclear stability on a classical electrodynamics foundation. Sections 23-25 are largely complete, but I still have more to develop in this part of the paper.

So that is where things stand as I pass the six week mark since I started writing this paper 140 pages ago.

Jay

[Yablon]

I just posted an update at https://jayryablon.files.wordpress.com/ ... -3-spf.pdf.

Sections 21 and 22 of what I posted the other day nagged at me because something did not add up, and it turns out I made the tidal force analysis way more complicated than it needed to be, and wrong.

I believe sections 19-22 in the attached are pretty much a wrap on Part III, and I think it is all correct now. Not to mention much simpler.

Section 22 is where I make may arguments as to why this paper is right in view of how one approaches spacetime curvature. In many ways, it is sections 7 and 22 that contain the arguments to answer the tough questions from I expect from editors and referees when I finally have this work ready to submit.

My plan now is to clean up sections 14 and 16 and the end of Part IV, then with one more proofread and this should be good to go.

Any comments, questions, critiques, suggestions are welcome.

Jay

[Ben6993]

Hi Jay

I was listening to the BBC Radio last night : Great Lives: about a pioneer of antiseptic medical procedures, Ignaz Semmelweis.
Apparently he was an enthuiast for hand washing who could not get his ideas, and practical results, accepted by the establishment, some 20 years before Lister's work.
http://www.bbc.co.uk/programmes/b0076ybp

There were two experts on the radio, one of whom frustratedly blamed Ignaz for not being able to get his ideas accepted! So there you are. You can bang your head against an impervious establishment wall and much later get the blame posthumously for not getting your point across well enough!!!
A second expert gave advice on what he should have done to be more persuasive. That was basically to get many more supporters of his ideas onside before banging his head.

I have just read something which links up with that idea at https://www.quantamagazine.org/20160303 ... al-dreams/
Michael Atiyah is apparently "Britain’s mathematical pope"?

The following extract from quanta magazine may be relevant. It depends on how novel it is to apply gravitation to atomic phenomena. I am thinking of your last page where you say you are giving classical gravitation reasons why the electron does not spiral into the proton nucleus. Apologies if I am getting this wrong but it seems to me to meet exactly what Michael is quoted [below] as thinking about in general terms. A potential supporter!?

Quote from Quanta magazine: "So you’re saying that the gravitational force can’t be ignored?

I think all the difficulty physicists have had comes from ignoring that. You shouldn’t ignore it. And the point is, I believe the mathematics gets simplified if you feed it in. If you leave it out, you make things more difficult for yourself.

Most people would say you don’t need to worry about gravitation when you look at atomic physics. The scale is so small that, for the kind of calculations we do, it can be ignored. In some sense, if you just want answers, that’s correct. But if you want understanding, then you’ve made a mistake in that choice.

If I’m wrong, well, I made a mistake. But I don’t think so. Because once you pick this idea up, there are all sorts of nice consequences. The mathematics fits together. The physics fits together. The philosophy fits together.

What does Witten think of your new ideas?

Well, it’s a challenge. Because when I talked to him in the past about some of my ideas, he dismissed them as hopeless, and he gave me 10 different reasons why they’re hopeless. Now I think I can defend my ground. I’ve spent a lot of time thinking, coming at it from different angles, and coming back to it. And I’m hoping I can persuade him that there is merit to my new approach."

[Yablon]

To all:

The reply below was sent along privately from a person who does not want to directly participate in the public discussions. So I am providing that reply here without that person's identity.

I have had a chance to analyze what our anonymous guest is saying. He is right about the error in (6.12), and that has been there since the late December draft where he did not see the error but it was there.

In fact, when I originally did the Lorentz force derivation, I thought this would add an extra term to the Lorentz force law, but because of the "zero" he said is wrong which is wrong, I did not have this extra term in there. But this person did correctly pinpoint the part of the derivation that gave me the most agita originally, so I was indeed happy that someone dug deeply enough the ferret this out and not surprised that this is where he focused.

Consequently, there IS an extra term in the Lorentz force that I have been neglecting. However, apropos to his other point about the potentials, I can gauge that extra term out as unobservable, and so get that term to zero by a different route and still have the Lorentz force law intact. So we live to fight another day, as they say! I will post a draft with the updated details of this over the weekend.

One other point in reply: the metric tensor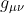 , like the gauge potential 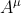, is also not unique because it too is subject to a symmetric gauge transformation using the local vector parameter in the combination . But this does not bar us from having this gauge-able gravitational potential in the expression for the metric interval 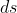nor does it ruin the invariant meaning of this interval.

Jay

Dear Mr. Yablon,

I tried several times to download the latest 140-page version of your paper "On the Geometric Foundations of Classical Electrodynamics", but every time the same thing happened: After few hundred kilobytes downloaded, the download failed because of an unspecified "network error". Previously, I had successfully downloaded the January 26 42-page version, so the following comments will refer to that version.

I think there is a serious mistake (actually, several) in its equation (6.12), which invalidates the paper's main claim that its methods imply a geometric derivation of the general relativistic equation of motion for a classical charged particle. Following is (6.12):



First of all, I question the passage from to . It looks as if you transferred the dummy integration symbol to the "numerator" of the differential operator , but this would not be legitimate. Even if it were legitimate, the next equation (" ") would not follow.

The reason that I think that this is an error rather than my inability to guess the reasons for the steps is that I think the following is an actual counterexample to (6.12). Consider any potential in Minkowski space for which and for spatial indices . For example, with for . If you want to make bounded with compact support, (which is often implicitly assumed in physics discussions), cut it off to make it bounded and smooth appropriately. Then the integral on the left of (6.12) becomes



which clearly will not vanish for all variations satisfying the variational boundary conditions .

It may save you some aggravation to carefully examine 6.12) before submitting the paper. Regardless of its merits, it will almost certainly be rejected anyway because of its length, but the rejection may be for some spurious pretext. I would be surprised if most referees would read it carefully enough to spot the error in (6.12).

An earlier December 30 version obtains by another method the usual Lorentz equation in curved spacetime. I didn't notice any error in the earlier version, though I haven't tried to check it carefully. You could revert to that earlier
method, but I don't think it would be worth the effort for the following reasons.

Personally, I don't consider either method to be either "geometric", or a "derivation" which provides any fundamental insight. (I have the same opinion about the much-discussed Kaluza-Klein (KK) "derivation", so clearly my view is not generally accepted; you are in good company!) The reason is that both your new metrics and KK's involve the 4-potential A, which (classically) is considered to be unobservable. That is because it is not unique --- if one potential yields the field tensor F, then adding to it the (four-dimensional) gradient of a function gives another potential which yields the same F.

So, the potential is not like the quantities associated with Einstein's metric such as the proper time along a worldline. You can measure the proper time by carrying a clock, but there is no instrument which can measure the electromagnetic potential.

I can't see how writing down a mathematical expression such as a Lagrangian (which is basically the starting point for your December 30 version) and finding the equation of motion which extremizes it provides any physical insight. It seems to me to be just sterile calculation. One chooses the Lagrangian to obtain the equation of motion that one believes to be physically correct. If one doesn't already know the physically correct equation, guessing a Lagrangian and deriving one doesn't yield an equation on which one would confidently bet!

Your January 26 version well illustrates this. Its Lagrangian-like expression is a reasonable thing to try, but it yields the wrong equation of motion (after correcting the errors). The Lagrangian that the Dec. 30 version uses (which incidentally is well known and essentially in every electromagnetic text which discusses Lagrangians) does yield the correct equations, but is no more well-motivated than the Jan. 26 Lagrangian.

Before closing, I'd like to say that I am sorry the tone of the above is necessarily negative, because it deals with mistakes. I did find interesting things in your paper, such as the discussion of how electromagnetic forces may prevent someone standing on the earth from falling through it. I had never thought of that! I don't know if your explanation is correct (because the classical picture of an atom as a nucleus orbited by electrons is just a picture not well supported by quantum mechanics), but it provides food for thought. I am taking the time to write this in the hope that it may give you food for thought, in return for that which you have given me. Thank you!

[Yablon]

Hi Jay
... I have just read something which links up with that idea at https://www.quantamagazine.org/20160303 ... al-dreams/
Michael Atiyah is apparently "Britain’s mathematical pope"? ...

Hi Ben, I very much enjoyed that article,and another one it linked about about Freeman Dyson at https://www.quantamagazine.org/20140326 ... ut-a-ph-d/ Very incisive articles. Jay

[Yablon]

...I think there is a serious mistake (actually, several) in its equation (6.12), which invalidates the paper's main claim that its methods imply a geometric derivation of the general relativistic equation of motion for a classical charged particle. Following is (6.12):



First of all, I question the passage from to . It looks as if you transferred the dummy integration symbol to the "numerator" of the differential operator , but this would not be legitimate. Even if it were legitimate, the next equation (" ") would not follow.

As I mentioned yesterday, this is a valid critique, and the referenced equation (6.12) was in error. I have now posted an updated draft which corrects this, at:

https://jayryablon.files.wordpress.com/ ... -2-spf.pdf

You will see that the former (6.12) is gone entirely. This extra term does not zero out automatically by identity, but rather carries through into the equation of motion now at (6.16). But, we may now subject the equation of motion to a local gauge transformation, and the only term which is not symmetric under the transformation will be that new term. However, we may impose the gauge condition (6.18) on this new, unobservable term so as to zero this out, thereby recovering the general relativistic equation of motion for a classical charged particle in what is now (6.19). So the paper's main claim remains intact, but now we use a gauge condition to zero this term rather than the former erroneous (6.12).

Many thanks to our anonymous guest for pointing this out. (If our guest or anybody else has trouble downloading from https://jayryablon.files.wordpress.com/ ... -2-spf.pdf please let me know and I will get the PDF file over to you in some other way.)

Jay