Response to the Gill Challenge
39 posts
• Page 1 of 2 • 1, 2
Response to the Gill Challenge
In response to Dr. Richard Gill's post of April 25, 2014
viewtopic.php?f=6&t=46
and his open challenge announced May 2, 2014
viewtopic.php?f=6&t=52#p1898
I hereby submit an 828KB compressed file, Directions.zip located at
http://geohologram.com/GillChallenge/Directions.zip
This file contains two files, AliceDirections.txt and BobDirections.txt which record the results of simulating Dr. Christian's thought experiment. Each of the lines in each .txt file contains one number, to be interpreted as an azimuthal angle in degrees (the simulation was done in the equatorial plane). You will notice that the values on corresponding lines are within a few degrees but not identical to each other, perhaps reflecting the difficulty Alice and Bob had in accurately measuring the angular momentum with the technology available to them.
In accordance with the Gill Challenge, correlations will be computed for four combinations of angles a (0 and 90 degrees) vs. b (45 and 135 degrees), by selecting a value for a and a value for b, and then running through both files concurrently.
For each line of the two files the two quantities
A_k = sign(a . u_k)
and
B_k = sign(b . v_k)
will be compared to measure the correlation.
Using the ordinary "flatland" dot product we expect to see classical correlations. In order to test Dr. Christian's theory (which is the point to the exercise) we will use his "sphereland" version of the dot product. This version generally gives the same value as the flatland version, but from time to time returns 0 instead. For clarity, here is the java implementation of this "sdotProduct":
static double sdotProduct( Point3D a, Point3D b )
{
double ab = a.dotProduct(b); // flatland dot product
return Math.abs(ab) < -1.0 + (2.0/Math.sqrt(1.0 + 3.0 * Math.random())) ? 0.0 : ab;
}
The correlation statistic to be calculated is given as:
E(a, b) = 1/N sum_k A_k B_k
This is fine for ordinary dot products which rarely return 0, but in sphereland, the sdotProduct often returns 0 and we will need to adjust the 1/N pre-factor to accomodate the 0 results. We will use the customary method to handle zeros when they occur, which is to subtract the 0 results from the denominator, as described here:
http://en.wikipedia.org/wiki/Quantum_correlation
These two changes to the flatland algorithm will give us the sphereland correlations, according to Dr. Christian's theory, and we can compare those to the terms of the challenge. Of course, anyone (not just Dr. Gill) is welcome to download the file, run the test, and report what they find.
Aloha,
Hugh Matlock
Princeton, NJ
viewtopic.php?f=6&t=46
and his open challenge announced May 2, 2014
viewtopic.php?f=6&t=52#p1898
I hereby submit an 828KB compressed file, Directions.zip located at
http://geohologram.com/GillChallenge/Directions.zip
This file contains two files, AliceDirections.txt and BobDirections.txt which record the results of simulating Dr. Christian's thought experiment. Each of the lines in each .txt file contains one number, to be interpreted as an azimuthal angle in degrees (the simulation was done in the equatorial plane). You will notice that the values on corresponding lines are within a few degrees but not identical to each other, perhaps reflecting the difficulty Alice and Bob had in accurately measuring the angular momentum with the technology available to them.
In accordance with the Gill Challenge, correlations will be computed for four combinations of angles a (0 and 90 degrees) vs. b (45 and 135 degrees), by selecting a value for a and a value for b, and then running through both files concurrently.
For each line of the two files the two quantities
A_k = sign(a . u_k)
and
B_k = sign(b . v_k)
will be compared to measure the correlation.
Using the ordinary "flatland" dot product we expect to see classical correlations. In order to test Dr. Christian's theory (which is the point to the exercise) we will use his "sphereland" version of the dot product. This version generally gives the same value as the flatland version, but from time to time returns 0 instead. For clarity, here is the java implementation of this "sdotProduct":
static double sdotProduct( Point3D a, Point3D b )
{
double ab = a.dotProduct(b); // flatland dot product
return Math.abs(ab) < -1.0 + (2.0/Math.sqrt(1.0 + 3.0 * Math.random())) ? 0.0 : ab;
}
The correlation statistic to be calculated is given as:
E(a, b) = 1/N sum_k A_k B_k
This is fine for ordinary dot products which rarely return 0, but in sphereland, the sdotProduct often returns 0 and we will need to adjust the 1/N pre-factor to accomodate the 0 results. We will use the customary method to handle zeros when they occur, which is to subtract the 0 results from the denominator, as described here:
http://en.wikipedia.org/wiki/Quantum_correlation
These two changes to the flatland algorithm will give us the sphereland correlations, according to Dr. Christian's theory, and we can compare those to the terms of the challenge. Of course, anyone (not just Dr. Gill) is welcome to download the file, run the test, and report what they find.
Aloha,
Hugh Matlock
Princeton, NJ
- Hugh Matlock
- Posts: 3
- Joined: Thu May 22, 2014 2:54 pm
Re: Response to the Gill Challenge
Hi Hugh,
I haven't checked your files yet, but your logic seems good to me (although I am puzzled by the "<" instead of ">" in it):
For those not well-versed in the Java script, this is an implementation of what is usually referred to as exploiting the "detection loophole" in the Pearle's model.
In my view that, unfortunately, is a wrong interpretation of what is going on. Correctly interpreted, the above constraint is simply a constraint arising from the topology of the 3-sphere:
\,}\;}\;,\;\;{\rm with}\;\, \theta_o\,\in\,[0,\;\pi]) ,
,
where specifies the "direction" of the spin angular momentum and
specifies the "direction" of the spin angular momentum and 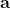 is any "freely chosen" axis of measurement.
is any "freely chosen" axis of measurement.
For a theoretical analysis of the above constraint, please see my latest paper on the subject, together with these two simulations.
So, from the theoretical perspective your entry looks good to me. But I would like to understand its relation to my calculations.
I haven't checked your files yet, but your logic seems good to me (although I am puzzled by the "<" instead of ">" in it):
Hugh Matlock wrote:static double sdotProduct( Point3D a, Point3D b )
{
double ab = a.dotProduct(b); // flatland dot product
return Math.abs(ab) < -1.0 + (2.0/Math.sqrt(1.0 + 3.0 * Math.random())) ? 0.0 : ab;
}
For those not well-versed in the Java script, this is an implementation of what is usually referred to as exploiting the "detection loophole" in the Pearle's model.
In my view that, unfortunately, is a wrong interpretation of what is going on. Correctly interpreted, the above constraint is simply a constraint arising from the topology of the 3-sphere:
where
For a theoretical analysis of the above constraint, please see my latest paper on the subject, together with these two simulations.
So, from the theoretical perspective your entry looks good to me. But I would like to understand its relation to my calculations.
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Response to the Gill Challenge
Thank you for your submission, Hugh!
The dot product mentioned in the challenge is definitely the flatland dot product. There are no zero outcomes, either.
Your simulation is apparently a simulation of the Pearle (1970) detection loophole model. The rather pretty formula generating the "non-detections" with the square root and the numbers 2 and 3 was recently discovered by myself - I think I was the first person in 40 years to decode Pearle's calculus and convert it into a simple computer algorithm. It is really elegant. A masterpiece.
The challenge is built on Christian's two "experimental papers" which give rather precise instructions to experimenters and to their lab technicians, IT specialists and so on, as how to process two large data files containing directions of angular momentum of spinning exploding hemispheres (whose paths were captured on video film).
The instructions always seemed to me to be crystal clear, unambiguous.
Perhaps Christian would like to revise his experimental papers removing this ambiguity.
If he would like to admit that the challenge itself is ambiguously formulated (it deliberately does not presuppose knowledge of Christian's theory) then I will retract it, and we will enter into a new period of negotiations and attempt to formulate an unambiguous and meaningful challenge.
The dot product mentioned in the challenge is definitely the flatland dot product. There are no zero outcomes, either.
Your simulation is apparently a simulation of the Pearle (1970) detection loophole model. The rather pretty formula generating the "non-detections" with the square root and the numbers 2 and 3 was recently discovered by myself - I think I was the first person in 40 years to decode Pearle's calculus and convert it into a simple computer algorithm. It is really elegant. A masterpiece.
The challenge is built on Christian's two "experimental papers" which give rather precise instructions to experimenters and to their lab technicians, IT specialists and so on, as how to process two large data files containing directions of angular momentum of spinning exploding hemispheres (whose paths were captured on video film).
The instructions always seemed to me to be crystal clear, unambiguous.
Perhaps Christian would like to revise his experimental papers removing this ambiguity.
If he would like to admit that the challenge itself is ambiguously formulated (it deliberately does not presuppose knowledge of Christian's theory) then I will retract it, and we will enter into a new period of negotiations and attempt to formulate an unambiguous and meaningful challenge.
- gill1109
- Mathematical Statistician
- Posts: 2812
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: Leiden
Re: Response to the Gill Challenge
Dr. Gill,
Your remark "(it deliberately does not presuppose knowledge of Christian's theory)" is curious given that the challenge is a call to model, through computer simulation, the theory that Dr. Christian describes in his paper. An implementor would reasonably be expected to read the paper before getting down to work. So that would presumably give them at least a basic "knowledge of Christian's theory."
I think the dispute between you and Dr. Christian (which the bet and challenge is meant to address) comes into a sharp focus in the choice of the analytical method for interpreting the data files. What methodological framework is appropriate for analyzing the results of the simulation?
Any such an interpretive framework rests on a theory (i.e. a mathematically precise description how the world works) which interprets what the experimental data is measuring. With carefully designed experiments (and even thought experiments and simulations) we can compare the usefulness of different theories, e.g. Newton's gravity vs Einstein's gravity, to see which one might be most effective at given scales in time and space.
In the same way, current quantum theory on E3 and Christian's model on S3, (a.k.a. flatland and spaceland) can be used to interpret the events in the physical world. We do not know for sure if the physical world is best described with an E3 or S3 geometry, and it may be hard to tell, since locally they are very similar (e.g. you can find three orthogonal directions from any point). But they are different globally as E3 is open and S3 is closed. And you have a difference in torsion, which (for example) the theory of teleparallel gravity exploits.
Dr. Christian's theory is one way of exploring this E3/S3 question locally. But is his theory useful at quantum scales, macroscopic scales or both? Having shown (albeit controversially) that his theory can provide a local realistic model for quantum scale events, he also now proposes it might work for macroscopic events. The Gill Challenge, as I understand it, was meant to explore this macroscopic question.
Using either a new or an established theory we can build simulations and compare them against our expectations. But we must be careful not to switch horses midstream. It is necessary to utilize analytical methods appropriate to each framework individually, and remain consistent when gathering and analyzing data in an experiment (whether real or simulated or imagined).
Whenever we get a chance to do a real experiment, we can see whether a theory succeeded to correctly predict the operation of Nature. Over time, a successful new theory might make predictions that work where an old theory failed. This new theory might eventually supplant the old, as its wider applicability becomes evident. Such a process is the source of progess in science, when the exploration and testing of new ideas is encouraged.
A reasonable interpretation of the challenge would not preclude the use of Dr. Christian's theoretical framework, and thus the potential for discovery of something novel. I doubt Dr. Christian would have collaborated in the protocol if he did not think it was phrased in a balanced way to give his theory and methods a fair hearing. And precluding new science is clearly not your intent either, as your Apr 27 comment shows:
Comment by gill1109:
"There is no humiliation in science. It is a collective enterprise of humanity. If Joy wins I will be amazed, temporarily short of cash, and delighted to witness the birth of a new age of science."
viewtopic.php?f=6&t=46
Aloha,
Hugh
Your remark "(it deliberately does not presuppose knowledge of Christian's theory)" is curious given that the challenge is a call to model, through computer simulation, the theory that Dr. Christian describes in his paper. An implementor would reasonably be expected to read the paper before getting down to work. So that would presumably give them at least a basic "knowledge of Christian's theory."
I think the dispute between you and Dr. Christian (which the bet and challenge is meant to address) comes into a sharp focus in the choice of the analytical method for interpreting the data files. What methodological framework is appropriate for analyzing the results of the simulation?
Any such an interpretive framework rests on a theory (i.e. a mathematically precise description how the world works) which interprets what the experimental data is measuring. With carefully designed experiments (and even thought experiments and simulations) we can compare the usefulness of different theories, e.g. Newton's gravity vs Einstein's gravity, to see which one might be most effective at given scales in time and space.
In the same way, current quantum theory on E3 and Christian's model on S3, (a.k.a. flatland and spaceland) can be used to interpret the events in the physical world. We do not know for sure if the physical world is best described with an E3 or S3 geometry, and it may be hard to tell, since locally they are very similar (e.g. you can find three orthogonal directions from any point). But they are different globally as E3 is open and S3 is closed. And you have a difference in torsion, which (for example) the theory of teleparallel gravity exploits.
Dr. Christian's theory is one way of exploring this E3/S3 question locally. But is his theory useful at quantum scales, macroscopic scales or both? Having shown (albeit controversially) that his theory can provide a local realistic model for quantum scale events, he also now proposes it might work for macroscopic events. The Gill Challenge, as I understand it, was meant to explore this macroscopic question.
Using either a new or an established theory we can build simulations and compare them against our expectations. But we must be careful not to switch horses midstream. It is necessary to utilize analytical methods appropriate to each framework individually, and remain consistent when gathering and analyzing data in an experiment (whether real or simulated or imagined).
Whenever we get a chance to do a real experiment, we can see whether a theory succeeded to correctly predict the operation of Nature. Over time, a successful new theory might make predictions that work where an old theory failed. This new theory might eventually supplant the old, as its wider applicability becomes evident. Such a process is the source of progess in science, when the exploration and testing of new ideas is encouraged.
A reasonable interpretation of the challenge would not preclude the use of Dr. Christian's theoretical framework, and thus the potential for discovery of something novel. I doubt Dr. Christian would have collaborated in the protocol if he did not think it was phrased in a balanced way to give his theory and methods a fair hearing. And precluding new science is clearly not your intent either, as your Apr 27 comment shows:
Comment by gill1109:
"There is no humiliation in science. It is a collective enterprise of humanity. If Joy wins I will be amazed, temporarily short of cash, and delighted to witness the birth of a new age of science."
viewtopic.php?f=6&t=46
Aloha,
Hugh
- Hugh Matlock
- Posts: 3
- Joined: Thu May 22, 2014 2:54 pm
Re: Response to the Gill Challenge
Hugh Matlock wrote:Dr. Gill,
Your remark "(it deliberately does not presuppose knowledge of Christian's theory)" is curious given that the challenge is a call to model, through computer simulation, the theory that Dr. Christian describes in his paper. An implementor would reasonably be expected to read the paper before getting down to work. So that would presumably give them at least a basic "knowledge of Christian's theory."
Dear Hugh
The challenge in question is not based on Christian's theoretical work but on his experimental paper. The paper includes instructions to lab technicians and IT specialists on how to process the data coming out of that experiment. You are the first person ever to suggest that the dot product between ordinary real vectors mentioned in that paper is anything except the familiar scalar product of real 3-vectors. And the inner-product which you now put forward was not even invented when Christian wrote his experimental paper!
So the discussion is very interesting and who knows, maybe leads somewhere exciting, but the challenge is still open.
Alternatively, if Joy wants to revise his experimental papers in order to clarify what dot product is meant, that would be a step forwards. Depending on the revision, there might or might not be a possibility to design a new educational challenge.
Of course, the actual point of the existing challenge (based on the current version of Christian's experimental paper) is that it is impossible to win it. Yet it was drawn up by myself and Joy Christian in open collaboration. One of his supporters, Michel Fodje, even told him that he was certain to lose.
- gill1109
- Mathematical Statistician
- Posts: 2812
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: Leiden
Re: Response to the Gill Challenge
gill1109 wrote:Of course, the actual point of the existing challenge (based on the current version of Christian's experimental paper) is that it is impossible to win it. Yet it was drawn up by myself and Joy Christian in open collaboration. One of his supporters, Michel Fodje, even told him that he was certain to lose.
I have no idea what Richard intends to gain by constantly repeating lies. My objections to how he has been misinterpreting my proposed experiment are well documented, and can be found on these pages here and here. Michel's view on how Richard Gill operates can be found on this page here.
As for the dot product, it is simply a variant of the geometric product: (I.a)(I.b) = -a.b - I.(a x b). More pertinently, it is an inner product on the tangent space of S^3 rather than on the tangent space of R^3. Physically, it is more appropriate to see it as characterizing the geodesic distance on the group SU(2) rather than on the group SO(3), with the former being the double covering group of the latter. All these relationships are extensively discussed in this paper [see, especially, eqs. (114), (115), and (116)]. The reason why a non-trivial dot product is needed is simple. One can see the reason already in this geometric product. (I.a)(I.b) = -a.b – I.(a x b). But as I mentioned, the reasons are elaborately discussed in the above paper. The issue is that ordinary vectors live in the flat space R^3, whereas angular momentum, which is not an ordinary vector but a bivector, lives in the tangent space of S^3, which can be described only by graded basis or quaternionic numbers. This in fact goes back to the discussion in my very first paper of 2007. The fact that the dot product has to be non-trivial has also been explicitly discussed in my first “experimental” paper: http://arxiv.org/abs/0806.3078 (see, for example, the discussion towards the end of the first paragraph on page 2, column 1, of the paper).
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Response to the Gill Challenge
gill1109 wrote:O One of his supporters, Michel Fodje, even told him that he was certain to lose.
Of course, as can be expected from Richard Gill the above is another lie and misrepresentation. He is incapable of speaking truthfully about my position.
Joy Christian wrote:The issue is that ordinary vectors live in the flat space R^3, whereas angular momentum, which is not an ordinary vector but a bivector, lives in the tangent space of S^3, which can be described only by graded basis or quaternionic numbers.
Could you say that again, Joy.
- minkwe
- Posts: 1441
- Joined: Sat Feb 08, 2014 10:22 am
Re: Response to the Gill Challenge
The crux of the matter is that Richard doesn't seem to realize nor understand that in,
E(a, b) = 1/N sum_k A_k B_k
A_k B_k is necessarily a geometric product. Of course if one takes it as an ordinary product, there is no way to get the result -a.b. So if Richard is sticking to it being an ordinary product, he is once again "rigging the game". Joy has already won the challenge if one uses the geometric product.
E(a, b) = 1/N sum_k A_k B_k
A_k B_k is necessarily a geometric product. Of course if one takes it as an ordinary product, there is no way to get the result -a.b. So if Richard is sticking to it being an ordinary product, he is once again "rigging the game". Joy has already won the challenge if one uses the geometric product.
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Response to the Gill Challenge
minkwe wrote:Joy Christian wrote:The issue is that ordinary vectors live in the flat space R^3, whereas angular momentum, which is not an ordinary vector but a bivector, lives in the tangent space of S^3, which can be described only by graded basis or quaternionic numbers.
Could you say that again, Joy.
Let me do better. Let me post an introductory paragraph from my "experimental" paper, this one, to bring the point home:

I hope Richard doesn't just read this paragraph, but actually tries to understand it, in the context of Michel's comment.
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Response to the Gill Challenge
Anyone who wants to pick up 10 000 Euro from me (you have till June 11) needs to read the text of the challenge (elsewhere on this forum) and page 4 of the experimental paper http://arxiv.org/pdf/0806.3078v2.pdf
Yes, the last page of the paper. The page which is about an experiment.
The lambda_j are directions of angular momentum of macroscopic objects (spinning hemispheres). They are unit vectors in R^3. They have been extracted by image processing software from video film. The measurement directions a, a', b, b' are unit vectors in R^3. The dot is the dot product and "sign" is sign. There is one set of N directions for Alice, and another set for Bob. Read the text of the challenge, attentatively. A text agreed by Joy Christian. Notice the words "unit vectors in R^3".
If the author meant something completely different then he'd be advised to post a revision of the paper on arXiv. He certainly succeeded in making a fool of himself here. For weeks he's been submitting failed attempts using these notational conventions: dot product equals ordinary dot product, sign equals sign, directions are unit vectors in R^3, as he moreover agreed when we fixed the text of the challenge. Seems he finally realized it won't work that way. Because of the Nx4 spreadsheet theorem. Some kind of progress has been made, I believe.
PS Hugh Matlock's submission was legal, but unfortunately unsuccessful. But then it is a theorem that a successful submission is impossible. I'm surprised no-one seems to want to see the proof. But it is pretty trivial, to be sure.
Yes, the last page of the paper. The page which is about an experiment.
The lambda_j are directions of angular momentum of macroscopic objects (spinning hemispheres). They are unit vectors in R^3. They have been extracted by image processing software from video film. The measurement directions a, a', b, b' are unit vectors in R^3. The dot is the dot product and "sign" is sign. There is one set of N directions for Alice, and another set for Bob. Read the text of the challenge, attentatively. A text agreed by Joy Christian. Notice the words "unit vectors in R^3".
If the author meant something completely different then he'd be advised to post a revision of the paper on arXiv. He certainly succeeded in making a fool of himself here. For weeks he's been submitting failed attempts using these notational conventions: dot product equals ordinary dot product, sign equals sign, directions are unit vectors in R^3, as he moreover agreed when we fixed the text of the challenge. Seems he finally realized it won't work that way. Because of the Nx4 spreadsheet theorem. Some kind of progress has been made, I believe.
PS Hugh Matlock's submission was legal, but unfortunately unsuccessful. But then it is a theorem that a successful submission is impossible. I'm surprised no-one seems to want to see the proof. But it is pretty trivial, to be sure.
- gill1109
- Mathematical Statistician
- Posts: 2812
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: Leiden
Re: Response to the Gill Challenge
gill1109 wrote:The lambda_j are directions of angular momentum of macroscopic objects (spinning hemispheres). They are unit vectors in R^3. They have been extracted by image processing software from video film. The measurement directions a, a', b, b' are unit vectors in R^3. The dot is the dot product and "sign" is sign. There is one set of N directions for Alice, and another set for Bob. Read the text of the challenge, attentatively. A text agreed by Joy Christian. Notice the words "unit vectors in R^3".
What does that have to do with A_k B_k being a geometric product?
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Response to the Gill Challenge
By the way, I have declared myself the winner of the Gill challenge on my blog. Here is what I have posted:
Joy Christian wrote:
In addition to these simulations, I have recently won the 10,000 Euros offered by Richard Gill for theoretically producing the 2n angular momentum vectors,and
, appearing in the equation (16) of my proposed experiment (see also this page). He had claimed that it was mathematically impossible to produce such 2n vectors and had challenged me to produce them as a "proof of concept" for my proposed experiment. I defeated his challenge on the 3rd of May 2014 by explicitly producing the 2n vectors in these two simulations.
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Response to the Gill Challenge
FrediFizzx wrote:gill1109 wrote:The lambda_j are directions of angular momentum of macroscopic objects (spinning hemispheres). They are unit vectors in R^3. They have been extracted by image processing software from video film. The measurement directions a, a', b, b' are unit vectors in R^3. The dot is the dot product and "sign" is sign. There is one set of N directions for Alice, and another set for Bob. Read the text of the challenge, attentatively. A text agreed by Joy Christian. Notice the words "unit vectors in R^3".
What does that have to do with A_k B_k being a geometric product?
Exactly, Fred. You tell me. I am perplexed. The experimental paper, page 4, needs to be revised, and the challenge will have to be reformulated.
Imagine that the experiment has been done. A huge mass of video films has been processed. For N pairs of spinning hemispheres, two directions of angular momentum have been calculated and saved in two computer files.
Tell me: what format is used? What representation? Cartesian coordinates x, y, z of unit vectors in R^3? Spherical coordinates theta, phi (azimuth, zenith)? Or something else?
The experimental paper, page 4, states that we then calculate 1/N sum_j sign(a . lambda_j ) sign(b . -lambda_j).
Till a few days ago Christian agreed that the vectors a, b, lambda_j, -lambda_j were unit vectors in R^3, the dot signified the usual scalar product, and sign meant sign.
Now Hugh Matlock has proposed an alternative definition involving an auxiliary randomization to "lift" the vectors lambda into the Pearle model. His random sign function often delivers a zero, and "1/N" is replaced by the number of positive terms. Clever idea, but at the time of the experimental paper Joy had never even read the Pearle paper. Christian specified "1/N" not "1 / # positive terms".
Joy Christian came up with an amusing new solution whereby each direction is replaced by two directions u and v, and whether Bob uses his u or his v in calculating sign(b . v) depends on whether Alice's direction a is 0 degrees or 90 degrees in the equatorial plane. So if Alice would measure in even more different directions, Bob would also need a w, x, y, z, ... and the representation of the direction of angular momentum of his hemisphere depends on which direction a Alice looks at hers.
We also heard Joy's statement that vectors u and v specify the same direction if u.v = 1.
This has become quite a farce. The experimental paper has disintegrated into hundreds of chaotically spinning fragments. Christian needs help rewriting page 4. The challenge is put on hold while we wait for a new version of the experimental paper which explains exactly what the experimentalist's IT assistants are supposed to do.
- gill1109
- Mathematical Statistician
- Posts: 2812
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: Leiden
Re: Response to the Gill Challenge
gill1109 wrote:Joy Christian came up with an amusing new solution whereby each direction is replaced by two directions u and v, and whether Bob uses his u or his v in calculating sign(b . v) depends on whether Alice's direction a is 0 degrees or 90 degrees in the equatorial plane.
No problem; that is what you have to do since A_k B_k is a geometric product. Did Joy ever say that it wasn't a geometric product? I doubt that very much since his model depends on it.
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Response to the Gill Challenge
Page 4 of my experimental paper contains only two unambiguous equations:

Here it is important to recall that

Note: There is only one correlation function, E(a, b), in equation (16), not four.
An introductory paragraph of the paper exposes the ambiguity in Bell's observables:

The following statement on my blog spells out the resolution of the Gill challenge:
In the second simulation I have used vectors) defined by the set
defined by the set
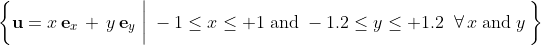
for calculating the first two of the four correlations in the simulation,
and vectors) defined by the set
defined by the set
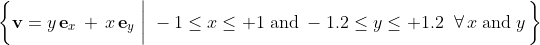
for calculating the last two of the four correlations in the simulation.
Richard Gill claims that these sets of vectors specify different sets of directions in the physical space. But evidently they specify exactly the same set of directions in the physical space. They both define a unique distribution of points on a circle of radius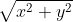 . This should be quite easy for any mathematician to see.
. This should be quite easy for any mathematician to see.

Here it is important to recall that

gill1109 wrote:
The experimental paper, page 4, states that we then calculate 1/N sum_j sign(a . lambda_j ) sign(b . -lambda_j).
...the vectors a, b, lambda_j, -lambda_j [are] unit vectors in R^3, the dot signified the usual scalar product, and sign [means] sign.
Note: There is only one correlation function, E(a, b), in equation (16), not four.
An introductory paragraph of the paper exposes the ambiguity in Bell's observables:

The following statement on my blog spells out the resolution of the Gill challenge:
Joy Christian wrote:
In addition to these simulations, I have recently won the 10,000 Euros offered by Richard Gill for theoretically producing the 2n angular momentum vectors,and
, appearing in the equation (16) of my proposed experiment (see also this page). He had claimed that it was mathematically impossible to produce such 2n vectors and had challenged me to produce them as a "proof of concept" for my proposed experiment. I defeated his challenge on the 3rd of May 2014 by explicitly producing the 2n vectors in these two simulations.
In the second simulation I have used vectors
for calculating the first two of the four correlations in the simulation,
and vectors
for calculating the last two of the four correlations in the simulation.
Richard Gill claims that these sets of vectors specify different sets of directions in the physical space. But evidently they specify exactly the same set of directions in the physical space. They both define a unique distribution of points on a circle of radius
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Response to the Gill Challenge
Joy Christian wrote:Page 4 of my experimental paper contains only two unambiguous equations:
Here it is important to recall thatgill1109 wrote:
The experimental paper, page 4, states that we then calculate 1/N sum_j sign(a . lambda_j ) sign(b . -lambda_j).
...the vectors a, b, lambda_j, -lambda_j [are] unit vectors in R^3, the dot signified the usual scalar product, and sign [means] sign.
Note: There is only one correlation function, E(a, b), in equation (16), not four.
An introductory paragraph of the paper exposes the ambiguity in Bell's observables:
The following statement on my blog spells out the resolution of the Gill challenge:Joy Christian wrote:
In addition to these simulations, I have recently won the 10,000 Euros offered by Richard Gill for theoretically producing the 2n angular momentum vectors,and
, appearing in the equation (16) of my proposed experiment (see also this page). He had claimed that it was mathematically impossible to produce such 2n vectors and had challenged me to produce them as a "proof of concept" for my proposed experiment. I defeated his challenge on the 3rd of May 2014 by explicitly producing the 2n vectors in these two simulations.
In the second simulation I have used vectorsdefined by the set
for calculating the first two of the four correlations in the simulation,
and vectorsdefined by the set
for calculating the last two of the four correlations in the simulation.
Richard Gill claims that these sets of vectors specify different sets of directions in the physical space. But evidently they specify exactly the same set of directions in the physical space. They both define a unique distribution of points on a circle of radius. This should be quite easy for any mathematician to see.
Let's distinguish sets from lists. A list is sometimes called an ordered set. People often colloquially use the word "set" when they mean "list"".
Suppose there are N exploding balls in the experiment. N sets of video films. Let's number them 1, 2, ..., N, say in the order the explosions were set off. Christian's experimentalist will have an IT support team who process these videos and generate from them two lists of length N of directions of angular momentum. See page 4 of the experimental paper. One list for Alice's hemispheres, one for Bob's.
Is everyone with me so far?
After that we can discuss the difference between a list of directions and a random sample from a set of directions. The difference between a probability distribution and a realization of a value taken at random from a distribution.
Christian might like also to specify how his experimentalist's IT specialists are to represent the direction of the angular momentum of some massive spinning object, whose motion has been captured on video film, and whose geometry and mass distribution is known in advance, I suppose.
Christian has a lot of explaining to do. My challenge is withdrawn till such time as a revision of the experimental paper is posted on arXiv. Christian has effectively revoked the present version of the paper, by revoking his agreement to the terms of the challenge. That's progress, of a kind. "Reculer pour mieux sauter". Good luck, there is quite a conundrum to be solved!
- gill1109
- Mathematical Statistician
- Posts: 2812
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: Leiden
Re: Response to the Gill Challenge
gill1109 wrote:Christian has a lot of explaining to do. The challenge is withdrawn till such time as a revision of the experimental paper is posted on internet.
I have no explaining to do. There is no reason to revise my paper. The contents of my paper are completely transparent and unambiguous.
As for the challenge (whose terms were unambiguously spelt out here by Richard Gill himself), it has been won by me already; resolved, done with, defeated:
Joy Christian wrote:
In addition to these simulations, I have recently won the 10,000 Euros offered by Richard Gill for theoretically producing the 2n angular momentum vectors,and
, appearing in the equation (16) of my proposed experiment (see also this page). He had claimed that it was mathematically impossible to produce such 2n vectors and had challenged me to produce them as a "proof of concept" for my proposed experiment. I defeated his challenge on the 3rd of May 2014 by explicitly producing the 2n vectors in these two simulations.
Note that I have posted the two .txt files of angular momentum directions, as required by Richard Gill, on this very forum, here (with further justification here).
Richard Gill owes me 10,000 Euros, period.
By the way, I will be adding interest and inflation adjustment to 10,000 Euros, starting from 1 June 2014. If Richard Gill does not pay up by 1 June 2014, then the interest and inflation adjustment will increase the amount until he pays up (since Richard has been changing the rules of the game, this caution seems necessary).
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
Re: Response to the Gill Challenge
gill1109 wrote:My challenge is withdrawn till such time as a revision of the experimental paper is posted on arXiv. Christian has effectively revoked the present version of the paper, by revoking his agreement to the terms of the challenge. That's progress, of a kind. "Reculer pour mieux sauter". Good luck, there is quite a conundrum to be solved!
Ahh... I figured you would back out of the challenge once you saw that Joy is right. You simply forgot that A_k B_k is a geometric product; always has been in Joy's model. Maybe now you will try to learn more about 3-sphere topology and geometry. One can only hope. There is nothing to revise and there is no conundrum to be solved. Joy's experiment is capable of producing the result of -a.b. Let's move forward on that.
- FrediFizzx
- Independent Physics Researcher
- Posts: 2905
- Joined: Tue Mar 19, 2013 7:12 pm
- Location: N. California, USA
Re: Response to the Gill Challenge
FrediFizzx wrote:gill1109 wrote:My challenge is withdrawn till such time as a revision of the experimental paper is posted on arXiv. Christian has effectively revoked the present version of the paper, by revoking his agreement to the terms of the challenge. That's progress, of a kind. "Reculer pour mieux sauter". Good luck, there is quite a conundrum to be solved!
Ahh... I figured you would back out of the challenge once you saw that Joy is right. You simply forgot that A_k B_k is a geometric product; always has been in Joy's model. Maybe now you will try to learn more about 3-sphere topology and geometry. One can only hope. There is nothing to revise and there is no conundrum to be solved. Joy's experiment is capable of producing the result of -a.b. Let's move forward on that.
Ah Fred, your comments are such a delight!
Problem is, it seems Christian can't read. I have for a long time been suspecting dyslexia. This explains everything...
The challenge explicitly specified that u, v, a and b are real three-vectors; a.u and b.v are the ordinary scalar products; and "sign" is the usual sign function. Moreover for quite a few weeks Christian was turning out one failed simulation after another which made use of those same conventions. However at last light has begun to dawn...
It seems to me that page 4 of his experimental paper badly needs to be rewritten, because as it stands, no-one is going to do the experiment, since it is certain to fail ... as both Christian and you now seem to realize.
Please help Christian re-write page 4 of the experimental paper so that the experimenter is told explicitly what to do in the final stage of data analysis. Let's move forward. This thread can be closed now, please start a new one.
- gill1109
- Mathematical Statistician
- Posts: 2812
- Joined: Tue Feb 04, 2014 10:39 pm
- Location: Leiden
Re: Response to the Gill Challenge
gill1109 wrote:Problem is, it seems Christian can't read. I have for a long time been suspecting dyslexia.
Can you read yourself, Richard?
Joy Christian wrote:Page 4 of my experimental paper contains only two unambiguous equations:
Here it is important to recall thatgill1109 wrote:
The experimental paper, page 4, states that we then calculate 1/N sum_j sign(a . lambda_j ) sign(b . -lambda_j).
...the vectors a, b, lambda_j, -lambda_j [are] unit vectors in R^3, the dot signified the usual scalar product, and sign [means] sign.
Note: There is only one correlation function, E(a, b), in equation (16), not four.
An introductory paragraph of the paper exposes the ambiguity in Bell's observables:
The following statement on my blog spells out the resolution of the Gill challenge:Joy Christian wrote:
In addition to these simulations, I have recently won the 10,000 Euros offered by Richard Gill for theoretically producing the 2n angular momentum vectors,and
, appearing in the equation (16) of my proposed experiment (see also this page). He had claimed that it was mathematically impossible to produce such 2n vectors and had challenged me to produce them as a "proof of concept" for my proposed experiment. I defeated his challenge on the 3rd of May 2014 by explicitly producing the 2n vectors in these two simulations.
It is very important to note that in the second simulation above I have used vectorsdefined by the ordered set
for calculating the first two of the four correlations in the simulation,
and vectorsdefined by the ordered set
for calculating the last two of the four correlations in the simulation.
Richard Gill claims that these sets of vectors specify different sets of directions in the physical space. But evidently they specify exactly the same set of directions in the physical space. They both define a unique distribution of points on a circle of radius. This should be quite easy for any mathematician to see, by
simply noting that.
and
are thus different names of one and the same spin direction (say
) in the physical space.
- Joy Christian
- Research Physicist
- Posts: 2793
- Joined: Wed Feb 05, 2014 4:49 am
- Location: Oxford, United Kingdom
39 posts
• Page 1 of 2 • 1, 2
Return to Sci.Physics.Foundations
Who is online
Users browsing this forum: ahrefs [Bot] and 104 guests

