Ben6993 wrote:Hi Gordon
My point about your paper was a very narrow one: that there is no error in dropping AA from the function being integrated.
Turning the problem from an integration into a discrete summation does not change this issue. λ must be held constant within the function until you are ready to do the discrete summation just as it should be held constant doing an integration.
….
[Ben's example], title added by GW: "Think of a calculation of the area under a curve given by function F. At point x = xi the area of a vertical strip under the curve is Fi times Δx. Where Fi is the value of F when x = xi. The integration is a sum of many such strips. Fi must be calculated at the point xi. When you are playing around with the form of Fi it should still be applicable only at point x=xi. It should not be a mix of what F is at x= xi and x=xj simultaneously. When you have a suitable form for Fi at x = xi, then you re-label Fi as F and xi as x and integrate Fdx."
In the broader issue of Bell's Inequality, I tend to side with Joy
.
Thanks Ben; it's good to see that:
A: in siding with Joy, you are open to answering "where did Bell (1964) go wrong?"
B: your focus in this post is a very narrow one: "that there is no error in dropping AA from the function being integrated."
C: as we'll see, you are close to making my point: AiAj ≠ 1 in general; and thus rejecting your assertion in B above.
To see why I've written C above, let's consider "Ben's example" (per my underlined edit above): and let's edit it as underlined below (for clarity, small obvious edits are not identified by underlining).
(Scene in Peru): Think of a calculation
by a Peruvian physicist of the area under a curve given by
some function F
whose domain is [a,b]. At point x = xi the area of a vertical strip under the curve is Fi times Δx. Where Fi is the value of F when x = xi. The integration is a sum of many such strips
Ai = FiΔx as i goes to infinity. Fi must be calculated at the point xi. When you are playing around with the form of Fi it should still be applicable only at point x=xi. It should not be a mix of what F is at x= xi and x=xj simultaneously. When you have a suitable form for Fi at x = xi [say, F(x) = 0.99999x], then you re-label Fi as F(x) and xi as x and integrate F(x)dx over [a,b].
(Scene in Paris): Think of a calculation
by a Parisian physicist of the area under a curve given by
some function G
whose domain is [a,b]. At point x = xj the area of a vertical strip under the curve is Gj times Δx. Where Gj is the value of G when x = xj. The integration is a sum of many such strips
Aj = GjΔx as j goes to infinity. Gj must be calculated at the point xj. When you are playing around with the form of Gj it should still be applicable only at point x=xj. It should not be a mix of what G is at x= xi and x=xj simultaneously. When you have a suitable form for Gj at x = xj [say, G(x) = 1.00001x], then you re-label Gj as G(x) and xj as x and integrate G(x)dx over [a,b].
Moral of the story:
(i): Two independently generated particle-pairs, like two independently generated curves, need not be the same. Moreover, why would they be the same? Worse: why would anyone insist that they be the same? Worse still: why would anyone
require them to be the same?
(ii): Why not set your analyses up (like I do in my essay) so that it is irrelevant whether two curves are the same or different?
(iii): Ben, please study and understand my Eqn (12). Do you there see, on LHS: that Bell and Peres and many others (with EIGHT subscripted
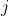
s)
require FOUR curves to be the same?
(iv): Ben, please: count what Bell, Peres, ++ require. Then think of Peru, Paris, Pisa, Pshaw!
Ben; are we there yet? At PSHAW?
With best regards; Gordon


