Dear Friends:
In an earlier thread, I started to explain at length, the basis upon which I had derived the quantum field potential which I am using, among other things,to analyze the single and double slit experiments. I had planned a Part I, Part II, etc. development of this, but I will go even one better:
In the past week, I have decided to write a new paper which consolidates my exact analytical solution to the Yang-Mills path integral in the simplest, most direct presentation possible. This solution is a
necessary prerequisite to solving the Yang-Mills and mass gap problem, because it proves the existence a non-linear quantum Yang-Mills theory in R^4. I plan in a few weeks when this is done, to submit this to a top journal, probably the same place where my very large paper is still sitting.
So because SPF is now in a new place which includes the capability to handle the display of Latex equations, I have decided that I will post drafts for each section of this paper as they are developed. And, I will ask anybody who is game to ask questions and provide whatever review or critique you believe is warranted. In this way, we will all conduct an experiment in which a foundational physics paper is developed with online review in a public forum, to see how well that goes. What is also nice about the formatting capabilities of this new group locale is that you can extract some specific section and put very visual quotes about it, and then zero in on that specific material for questions or critiques. I think this can be a much more effective means of having good discussion and understanding than having to refer to a separate PDF file. But if you do want to have the PDF also, that is here:
http://jayryablon.files.wordpress.com/2 ... al-1-0.pdf.
Unlike my earlier papers, I will make very liberal use of appendices for the detailed calculations, so that the main paper keeps the high-level development clear and crisp. So as part of your review, I'd like to know if the desired clarity is coming across to the reader. Below, I post the introduction which I wrote these past 48 hours, as well as Appendix B. (Appendix A is a to-be-added at the moment.)
My tentative title for this paper will be
Exact Analytical Solution of the Yang-Mills Path Integral using a Closed Recursive Kernel: On the Critical Path to the Mass Gap.
So, let the experiment begin:
1. IntroductionThe path integral formulation of quantum field theory, originally pioneered by Richard Feynman's considering multiple slit and screen experiments in the unscreened open-space limit where the number of slits and screens grows infinite, provides a very direct analytical link between any classical field theory and its quantum field counterpart [\footnote{[] Feynman, R. P., Space-Time Approach to Non-Relativistic Quantum Mechanics, Reviews of Modern Physics 20 (2): 367--387 (1948)}], [\footnote{[] Feynman, R. P. and Hibbs, A. R., Quantum Mechanics and Path Integrals, McGraw-Hill (1965)}]: Given any classical field theory with a generalized field

and source

and Lagrangian density
$)
thus classical action a.k.a. Lagrangian
\equiv \int d^{4} x{\rm {\mathcal L}}\left(\phi ,J\right) $)
, one simply uses a "path'' integral in which the position

of a particle in the measure

is replaced by a field
$)
in the measure

of what is effectively the "field'' integral
/\hbar \right)\equiv Z=\int D\phi \exp \left(iS\left(\phi ,J\right)/\hbar \right) =\int D\phi \exp \left(i\int d^{4} x{\rm {\mathcal L}}\left(\phi ,J\right) /\hbar \right) $)
. (1.1)
One then uses this to calculate a quantum action
$)
, also referred to as a quantum amplitude. This
$)
is simply the quantum field counterpart to the classical action
$)
, and each of these actions has the same mass

length^2 / time a.k.a. angular momentum dimensionality as Planck's constant

. By virtue of the field

being the variable of integration in the measure

, the field is stripped out during the path integration, which is why we obtain a
$)
and not a
$)
. In the classical limit where

, it is well known via stationary phase / steepest descent that the field integral (1.1) leads to the Euler-Lagrange equation
}{\delta \left(\partial _{\mu } \phi \right)} -\frac{\delta {\rm {\mathcal L}}\left(\phi ,J\right)}{\delta \phi } =0$)
, (1.2)
which is simply the classical field equation associated with the same Lagrangian density
$)
in (1.1) from which one obtains the quantum action
$)
.
So in view of this type of path / field integration, the recipe for going from a classical field theory to its quantum field theory counterpart,
in theory, is extremely straightforward: One starts with a classical field equation, such as the Maxwell equations for electrodynamics, the classical Yang-Mills field equations for weak or strong interactions, or the Einstein equation for gravitation. One first obtains whatever Lagrangian density

in needed to reproduce the classical field equation via (1.2). One then obtains the action

, plugs that into the path integral (1.1), does the integration, and as a result, comes away with a
$)
which specifies the quantum field theory. So from Maxwell's equations we arrive at a
$)
for quantum electrodynamics, from classical Yang-Mills field equations such as those for the weak and the strong interactions we arrive at quantum Yang-Mills theory which for the strong interaction yields a
$)
for quantum chromodynamics, and for gravitation we arrive at quantum gravitation via a
$)
. And that is that! The physics theory is easy.
But
in practice, it is a whole other story, because the
mathematics of calculating
$) exactly and analytically in closed form
exactly and analytically in closed form is extremely difficult. Indeed, for all except quantum electrodynamics, this mathematics has to date appeared intractable. The reason this analytical problem has not been solved to date, is precisely because classical Yang-Mills and classical gravitation are both
non-linear theories. In classical Yang-Mills theory, the gauge bosons

interact with each other and the action
$)
thus has non-quadratic field terms of order
G^3 and
G^4. Because of this, nobody has to date been able to solve the mathematical problem of analytically and exactly calculating the integral (1.1) in closed form. For gravitation, if one considers the Einstein-Hilbert action
=\int d^{4} x\sqrt{-g} \left[R/2+\kappa {\rm {\mathcal L}}_{M} \right] $)
which must go into (1.1) together which the way in which the Ricci scalar
R and

are related to the gravitational field represented in the metric tensor

, and the relationship

between the matter Lagrangian density

and the energy momentum tensor

, the challenge of analytically and exactly integrating (1.1) in closed form using
$)
and a measure

to obtain
$)
appears to be even steeper.
To see exactly why this is a problem, let us first review for contrast how it
is possible to exactly, analytically calculate the path integral (1.1) for electrodynamics, in closed form. We start with the electrodynamic action for a massive gauge boson of mass
m:
=\int d^{4} x{\rm {\mathcal L}} =\int d^{4} x \left({\tfrac{1}{2}} A_{\mu } \left[\left(g^{\mu \nu } \left(\partial _{\sigma } \partial ^{\sigma } +m^{2} \right)-\partial ^{\mu } \partial ^{\nu } \right)\right]A_{\nu } +A_{\mu } J^{\mu } \right)$)
, (1.3)
from which
$) can
can be exactly analytically calculated in closed form, via (1.1). First, if we use the
m=0 Lagrangian density
A_{\nu } +A_{\mu } J^{\mu } $)
contained in (1.3), in the Euler-Lagrange equation (1.2), then in view of the integration-by-parts which yields this

, we do indeed reproduce Maxwell's classical field equation

for an electric charge density

. This is reviewed in Appendix A.
Second, because the configuration space operator
-\partial ^{\mu } \partial ^{\nu } $)
contained in (1.3) does
not contain any appearances of the electromagnetic field

, we can treat this as a constant with respect to the integration over

in (1.1), so that (1.3) can be written in the simplified form:
=\int d^{4} x{\rm {\mathcal L}} =\int d^{4} x \left({\tfrac{1}{2}} A_{\mu } K^{\mu \nu } A_{\nu } +A_{\mu } J^{\mu } \right)$)
. (1.4)
This highlights that this action is quadratic in

, i.e., that it only has the term

which is of first order in
A, and

which is of second order in
A, i.e.,
A^2. There are no terms of any higher order in
A. So if we then use (1.4) in (1.1) with natural units

, we see that the integral we need to calculate is:
 \equiv {\rm C}\exp iW\left(J\right)$)
. (1.5)
So how do we calculate this?
Mathematically, we recognize that this has the basic form of the Gaussian integral:
=\left(2\pi i/K\right)^{.5} \exp \left(-iB^{2} /2K\right)$)
. (1.6)
So, if we momentarily ignore the

in (1.5), and we use (1.6) as a template by making the substitutions

,

,

and
^{.5} \to {\rm C}$)
, and if we then reintroduce the

along with the commensurate
^{4} $)
which arises from Fourier transforms between spacetime and momentum space, and if we finally use this as in (1.5) to define
$)
, then we obtain the result:
 ={\rm C}\exp \left(-\frac{1}{2} i\int \frac{d^{4} k}{\left(2\pi \right)^{4} } J^{\mu } \left(K^{\mu \nu } \right)^{-1} J^{\nu } \right)\equiv {\rm C}\exp iW\left(J^{\mu } \right)$)
. (1.7)
Now, from the final two terms, also recalling that
-\partial ^{\mu } \partial ^{\nu } $)
, we deduce:
=-\frac{1}{2} \int \frac{d^{4} k}{\left(2\pi \right)^{4} } J^{\mu } \left(K^{\mu \nu } \right)^{-1} J^{\nu } =-\frac{1}{2} \int \frac{d^{4} k}{\left(2\pi \right)^{4} } J^{\mu } \left(g^{\mu \nu } \left(\partial _{\sigma } \partial ^{\sigma } +m^{2} \right)-\partial ^{\mu } \partial ^{\nu } \right)^{-1} J^{\nu } $)
. (1.8)
That is it! The path integral is done, and have our quantum field action
$)
.
Of course, there is still an inverse
^{-1} \equiv \left(g^{\mu \nu } \left(\partial _{\sigma } \partial ^{\sigma } +m^{2} \right)-\partial ^{\mu } \partial ^{\nu } \right)^{-1} $)
to be calculated. Once that is done, and after we set the photon mass to zero, we arrive at the quantum amplitude for QED, which is:
=+\frac{1}{2} \int \frac{d^{4} k}{\left(2\pi \right)^{4} } J_{\sigma } \left(k\right)*\frac{1}{k_{\tau } k^{\tau } +i\varepsilon } J^{\sigma } \left(k\right) $)
. (1.9)
This is an exact, analytical, closed expression for
$)
. It is the positive overall sign in (1.9) which tells us that the electromagnetic interaction between two like-charges is repulsive. The steps by which one gets from (1.8) to (1.9) are reviewed in Appendix B, and (1.9) above is the same as (B.6).
So, now we arrive at the central question: how is it that we are able to get from the classical action
$)
in (1.3) to the quantum action
$)
of (1.9) for electrodynamics, in analytically-exact closed form, but are not able to do the same for Yang-Mills gauge theories which are simply a generalization of electrodynamics? The answer, of course, is that classical Yang-Mills theory is non-linear, which means that the classical action has terms which are of higher than second order in the gauge fields, and that the
mathematics of doing the path integration for such a non-linear action leading to a non-linear quantum field theory, has to date been intractable. Let us pinpoint the specific reasons why this is so, with an eye toward finally finding a solution to get past this intractability:
In Yang-Mills gauge theories, for which we symbolically denote the gauge fields as

in lieu of

, the action (1.3) now becomes:
=\int d^{4} x{\rm {\mathcal L}} =\int d^{4} x \left(G_{\mu } \left[\left(g^{\mu \nu } \left(D_{\sigma } D^{\sigma } +m^{2} \right)-D^{\mu } D^{\nu } \right)\right]G_{\nu } +2G_{\mu } J^{\mu } \right)$)
(1.10)
in which the ordinary derivative

is generalized into a gauge-covariant derivative

which does contain

, but also contains some

. The factor of 2 arises from the generator normalization

which is customarily applied to the generators

which form a closed group under multiplication via

, where

are the group structure constants and are antisymmetric under the transposition of any two adjacent indexes. For the special unitary subgroup group SU(
N), there are

gauge bosons

with

which sit in the adjoint representation of this gauge group, from which we define an

component matrix

. In fact, in (1.10), as we simply state for now and shall later derive in section ???:

(1.11)
which implies that
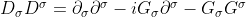
. (1.12)
So, using (1.11) and (1.12) in (1.10) so as to illustrate exactly how the

appear in the Yang-Mills action, we may write:
=\int d^{4} x{\rm {\mathcal L}} =\int d^{4} x \left(G_{\mu } \left[\left(-g^{\mu \nu } \left(iG_{\sigma } \partial ^{\sigma } +G_{\sigma } G^{\sigma } \right)+iG^{\mu } \partial ^{\nu } +2G^{\mu } G^{\nu } -G^{\nu } G^{\mu } \right)\right]G_{\nu } +G_{\mu } \left[\left(g^{\mu \nu } \left(\partial _{\sigma } \partial ^{\sigma } +m^{2} \right)-\partial ^{\mu } \partial ^{\nu } \right)\right]G_{\nu } +2G_{\mu } J^{\mu } \right)\])
(1.13)
Comparing this to (1.3), we see that the final term set does have exactly the same form as (1.3), and that the only difference is the factor of 2 from

and the symbolic use of

in lieu of

. So if we were to insert (1.13) into (1.1), and again use
-\partial ^{\mu } \partial ^{\nu } $)
as we earlier did in (1.4), then the counterpart to (1.5) which we now need to calculate is:
+iG^{\mu } \partial ^{\nu } +2G^{\mu } G^{\nu } -G^{\nu } G^{\mu } \right)\right]G_{\nu } +G_{\mu } \left[\left(g^{\mu \nu } \left(\partial _{\sigma } \partial ^{\sigma } +m^{2} \right)-\partial ^{\mu } \partial ^{\nu } \right)\right]G_{\nu } +2G_{\mu } J^{\mu } \right)\right) \equiv {\rm C}\exp iW\left(J^{\sigma } \right)\])
(1.14)
This still has the first and second order terms

and

as did (1.5.) But it also after reduction contains the third order terms

and the fourth order terms

, which is to say, this also contains terms of order
G^3 and
G^4 and so is a polynomial to fourth order in

. So whereas the integral (1.6) which we used as a template to obtain the QED action
$)
in (1.9) is based on the general Gaussian integral
=\left(2\pi /A\right)^{.5} \exp \left(B^{2} /2A\right)$)
, the exact, closed, analytical calculation of (1.14) requires us to have a template
$)
which contains a polynomial to the
fourth power of
x.
However, whereas
^{.5} \exp \left(B^{2} /2A\right)$)
is the closed form exact analytical solution to
$)
, we do
not know the exact analytical solution in closed form to
$)
.
This is, to date, an unsolved mathematical problem. And, neither do we know, to date, a closed form for the more specific Yang-Mills integral in which the polynomial

is the polynomial in

given by (1.14).
This too, remains to date, an unsolved mathematical problem. Indeed, even if we were to remove all of the third order terms by setting
D=0 in the polynomial, it is not even known how to exactly and analytically calculate the scalar path integral:
^{2} -m^{2} \phi ^{2} \right)-\left(\lambda /4\right)\phi ^{4} +J\phi \right) \equiv {\rm C}\exp iW\left(J\right)$)
, (1.15)
which is often referred to as the

problem because it is the term with

which renders this integral seemingly-incalculable. It will be appreciated that with the

term removed, the exact calculation, following the integration-by-parts of the
^{2} $)
term, would be readily solvable via the same path we took to obtain (1.9) via the Gaussian integral (1.6).
So the key challenge, as regards Yang-Mills theory, is to obtain an exact, closed, analytical solution to the path integral (1.14), which contains the classical action (1.10) with the gauge-covariant derivatives given (as we later derive in section ???) by (1.11) and (1.12). In this paper, we shall present the
mathematical solution for how to obtain
$)
in (1.14) in closed, exact analytical form. As we shall also establish, this is a necessary, indispensable first step to solving the Yang-Mills and Mass Gap Problem.
Appendix A -- to be addedAppendix BStarting at (1.8), we first calculate the inverse
^{-1} \equiv \left(g^{\mu \nu } \left(\partial _{\sigma } \partial ^{\sigma } +m^{2} \right)-\partial ^{\mu } \partial ^{\nu } \right)^{-1} $)
, which is simply the propagator
\left(g^{\mu \nu } \left(\partial _{\sigma } \partial ^{\sigma } +m^{2} \right)-\partial ^{\mu } \partial ^{\nu } \right)\equiv \delta ^{\mu } _{\alpha } \delta ^{\left(4\right)} \left(x\right)$)
(B.1)
Fourier transformed to momentum space via:
=\int \frac{d^{4} k}{\left(2\pi \right)^{4} } D_{\nu \alpha } \left(k\right)\exp \left(ik_{\sigma } x^{\sigma } \right)$)
. (B.2)
This is calculated with index renaming to be:
=\frac{-g_{\mu \nu } +k_{\mu } k_{\nu } /m^{2} }{k_{\tau } k^{\tau } -m^{2} } \left(=\left(K^{\mu \nu } \right)^{-1} \right)$)
. (B.3)
So when we use (B.3) in (1.8), and employ the square modulus

while explicitly denoting that these
$)
are in momentum space and so are related to the configuration space current densities by
\equiv \int d^{4} xJ^{\mu } \left(x\right)\exp \left(-ik_{\sigma } x^{\sigma } \right)$)
, and adding the

prescription, we find that:
=-\frac{1}{2} \int \frac{d^{4} k}{\left(2\pi \right)^{4} } J^{\mu } \left(k\right)*D_{\mu \nu } \left(k\right)J^{\nu } \left(k\right) =-\frac{1}{2} \int \frac{d^{4} k}{\left(2\pi \right)^{4} } J^{\mu } \left(k\right)*\frac{-g_{\mu \nu } +k_{\mu } k_{\nu } /m^{2} }{k_{\tau } k^{\tau } -m^{2} +i\varepsilon } J^{\nu } \left(k\right) $)
. (B.4)
Then, as a final step, observing that the charge conservation relationship
=0$)
gets Fourier transformed into
=0$)
in momentum space, we may simplify the above to:
=+\frac{1}{2} \int \frac{d^{4} k}{\left(2\pi \right)^{4} } J_{\sigma } \left(k\right)*\frac{1}{k_{\tau } k^{\tau } -m^{2} +i\varepsilon } J^{\sigma } \left(k\right) $)
. (B.5)
Because setting
m=0 in (B.3) and (B.4) causes

and thus
=\infty $)
in (B.4), we see that the momentum space operator

has no inverse. And we see that by including a non-zero mass, one can obtain a tame, non-singular inverse. But via the conservation equation
=0$)
, this term

is entirely removed
when it appears in the context of (B.4), and specifically, when the propagator is summed with the current in the form
J^{\nu } \left(k\right)$)
. Once we arrive at (B.5), we can set the boson mass to zero as is required for the photon, and this then yields the final QED amplitude shown in (1.9).
=+\frac{1}{2} \int \frac{d^{4} k}{\left(2\pi \right)^{4} } J_{\sigma } \left(k\right)*\frac{1}{k_{\tau } k^{\tau } +i\varepsilon } J^{\sigma } \left(k\right) $)
. (B.6)

